傅里叶变换及其应用三.复习，将一般周期函数表示为简单周期函数和

这份随笔是本人对B站斯坦福大学公开课：傅里叶变换及其应用 的学习笔记。

原课程网站：https://see.stanford.edu/Course/EE261

回顾

f(t)是一个周期为 1 的函数/信号

我们假定它可以用别的简单周期函数表示

\[f(t)=\sum _{k=-n}^n C_k e^{-2 \pi i k t} \]

其中 \(C_k\) 我们可以用一个明确的式子表示出来

\[C_k=\int_0^1 f (t) e^{-2 \pi i k t} \, dt \]

知道这个信号，就可以求出系数。而这个式子的推导过程中还有一个重要的表达式

\[e^{2 \pi i n t}-e^{-2 \pi i \text{mt}}= \begin{array}{cc} \{ & \begin{array}{cc} 0 & n\neq m \\ 1 & n=m \\ \end{array} \\ \end{array} \]

利用欧拉公式我们能很容易知道结果，这个表达式在后面还会再次提到。

前提条件

首先，我们先将 \(C_k\) 用这个学科中常用的形式替换一下：我们定义傅里叶系数为 f(k)，即

\[\hat{f} (k)=\int_0^1 f (t) e^{-2 \pi i k t} \, dt \]

前面是我们思考的第一步：假定这些周期性现象可以用这个式子建模。

第二步是：什么情况下，才能这样对这些周期性现象建模？

先举几个例子：

1）周期为1的矩形波信号：

我们可以计算出它的系数

\[\hat{f} (k)=\int_0^{\frac{1}{2}} e^{-2 \pi i k t} \, dt \]

那么我们能把这个矩形波信号写成有限的和的复指数形式吗？

\[\text{f(t)=} \sum _{k=-n}^n \hat{f} (k) e^{-2 \pi i k t} \]

不行！

对于有限和的形式是否定的，为什么？

因为有限和的复指数形式实际上是正余弦形式，他们是连续的，有限个连续函数的和仍然是连续的，它不可能表示一个离散现象，我们不可能用一个连续现象表示一个离散现象。

很明显，这很限制我们做信号处理。

2）周期为1的三角波信号

同样的我们计算出他的傅里叶系数，我们可以写成有限和的复指数形式吗？

\[\text{f(t)=} \sum _{k=-n}^n \hat{f} (k) e^{-2 \pi i k t} \]

不行！

两个可微分的函数，他们的和一定也是可微分的，但是三角函数不是可微分的，它有个拐点。

两边并不等价。

正余弦是无限可微分的，它的有限和不可能等于一个不是无限可微分的。

信号的任何导数的不连续性，都将建模不成立。

解决方法

潜在的准则：如果不能将 f(t) 表示成有限和的形式，那就必须把它表示成无限个和的形式。

它需要高频项来处理尖的拐角。

为了表示一般的周期性现象，我们必须对周期函数进行无限项求和。

当然，在实际问题中我们只能近似求和。

\[\text{f(t)=} \sum _{k=-\infty }^{\infty } \hat{f} (k) e^{-2 \pi i k t} \]

要注意的是，\(\hat{f} (k)\) 不一定都是非零数，它们中某些可能是0，比如矩形波，它只有奇数项。

任何非平滑的信号都会产生无限多个傅里叶系数。

收敛性

在数学（或者是应用）上计算一个无限求和的函数，我们就不得不考虑收敛的问题。如果它是收敛的，在有限项将它截断后得到的近似值，我们也想知道它有多么精确？如果它不收敛，在有限项将它截断后，还能得到我们想要的信号的合理近似值吗？所以我们不得不解决收敛的问题。

本课程不会去验证，而是直接给出两个结论：

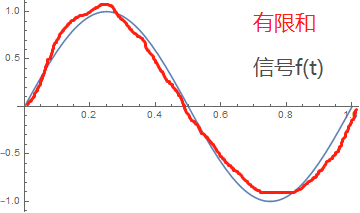
1）如果信号是平滑连续的，那么在任何连续点，级数的有限和都会收敛，均匀地接近给定函数。

我们叫它“逐点收敛”：选定一个“t”，将这些项加起来，结果就会收敛于 f(t)。

信号不同时刻 t ，级数和的收敛速率，取决于信号的平滑程度。平滑性越好，它收敛的越快，在有限的时间之内，有限的级数和 与 信号f(t)的误差越小。

这是平滑性带来的好处，我们可以估计这个平均误差的大小。进而得到在某个区间内，我们想要的合理近似值。

2）如果信号是跳变的，级数将会收敛于 跳变点处的前，后函数的平均值。

跳变是信号不连续情况之一，例如矩形波，设t0 点是跳变的不连续点

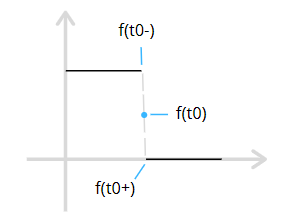
即

\[\sum _{k=-\infty }^{\infty } \hat{f} (k) e^{-2 \pi i k t} 在t0点收敛于 \frac{1}{2} \left(f (t^-)+f (t^+)\right) \]

实际应用

在一般实际应用中，我们并不使用逐点收敛的方法，不要去求特定点的收敛性问题，而是使用“均方收敛”的方法。

在工程上也叫做“能量收敛”。下一节解释原因。

不考虑连续性和平滑性，假定函数是周期函数，周期为 1。

均方收敛条件：函数 f(t) 的平方的积分有界。即

\[\int_0^1 \left| f (t)\right| ^2 \, dt<\infty \]

如果函数在一个周期内积分无限，明显不满足条件。它是基于能量是有限值的假设。这是一个合理的物理假设。

它不是通过特定点得到的，而是通过以下讨论的平均情况：

函数值与函数的近似值有多接近（意味着这是一个有限和）。

\[\int_0^1 \left|\sum _{k=-n}^n \hat{f} (k) e^{-2 \pi i k t}- f (t)\right| ^2 \, dt \]

当 n\(\rightarrow\) ∞ 时，结果会\(\rightarrow\) 0，证明 级数会收敛于 给定函数。

它与最小二乘逼近类似。

\[S_{\varepsilon ^2}=\sum _{a=1}^n \left(y-y_i\right){}^2 \]

式子中，\(S_{\varepsilon ^2}\) 为误差，\(y_i\)为实际值，y为猜测值。将各个误差的平法累加，当误差和最小时，拟合的曲线均匀逼近各实际值，平均距离最小，此时的拟合曲线最合适准确。

这里有个很有意思的讨论：误差有正有负，为了不相互抵消，用绝对值不就好了吗？为什么要把绝对值换成平方，平方能很好解决负数问题，而且方便求导。

如果我们对给定函数建模

\[\text{f(t)=} \sum _{k=-\infty }^{\infty } \hat{f} (k) e^{-2 \pi i k t} \]

其中等号不是意味着，取出一个时刻t，它的级数就会收敛于函数。它的意思是用均方收敛解释。这是在认识上一个很大的改变。