管流基础知识
本篇为国防科技大学公开课-传感器与测试技术的学习笔记。
在工农业中和科学实验中,需要检测各种流体的流量。如:水,油,空气,氢气等,并且随着科学技术发展,环境日益复杂,对流量测量的要求也越来越高。
定义
流体
具有流动性的液体或气体。
流量
指单位时间内流体(气体、液体或固体颗粒等)流经某一流通截面的数量,又称瞬时流量。
- 流体以体积表示时称为体积流量,单位为m3/s。
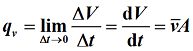
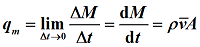
平均流速
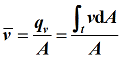
累计流量
在某段时间内流体通过的体积或质量总量,它是体积流量或质量流量在该段时间中的积分,表示为:
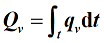
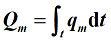
流体密度
单位体积的流体所具有的质量。体密度是温度和压力的函数,单位是(kg/m3)
粘滞力
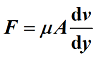
实际流体在流动时.其内部有相对运动的相邻两部分之间存在类似两固体相对运动时存在的摩擦阻力(内摩擦力)。
流体在流动的时候是分层的,每层流速不一样,比如在管道中流体运动,贴着管壁的是最慢的,流层之间有一个速度差,所以各层之间存在阻力,这个阻力就叫内摩檫力,又叫粘滞力。
式中:F为粘滞力;A为接触面积;
dv/dy为流体垂直于速度方向的速度梯度;
μ为表征流体粘性的系数(称为流体的粘度或粘滞系数)。
雷诺数Re
流体流动的惯性力与粘滞力之比。
雷诺数的大小决定了粘性流体的流动特性。
雷诺数小,流体流动时各质点间的粘性力占主要地位,流体各质点平行于管路内壁有规则地流动,呈层流流动状态。雷诺数大,惯性力占主要地位,流体呈紊流流动状态。
一般管道雷诺数Re<2000为层流状态,Re>4000为紊流状态,Re=2000~4000为过渡状态。
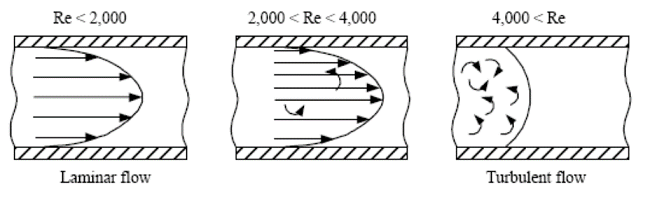
以下为来自知乎解释:
雷诺数是惯性力和粘性力的比,雷诺数越大,流体流动中惯性力的作用所占的比重越大,粘性效应占的比重越小,反应在建模型时,如果雷诺数很大,粘性效应可以忽略,那么就用理想流体Euler方程去模拟,如果雷诺数不那么大,粘性效应需要被考虑进去,那就是Navier-Stokes方程,说白了就是粘性效应在你考虑问题时的比重如何的事情。事实上湍流并不是高雷诺数激发的,而是扰动激发的。层流是流动的稳定状态,出现的扰动如果能够被抑制,流动就一直是稳定的层流;如果扰动无法被抑制,就会导致流动失稳,层流就转捩为湍流。(这里“稳定”、“扰动”的意思,和把一个圆球放在平面上、放在尖峰、放在谷底那个例子里的稳定性是一样的,扰动无处不在。)转捩和雷诺数有什么关系?理论上,求解Orr-Sommerferd方程会给出某种扰动下雷诺数多大会发生转捩。题主若有兴趣,可以看看这方面内容(讲湍流的书上都会有)。
从物理上“感受”的话,雷诺数比较小的时候,就是粘性比较大,外来的扰动容易被粘性“吃掉”、消耗为热能;当雷诺数比较大时,粘性抑制不住扰动,于是就失稳了。就像对着缓慢流动的黏糊糊的油吹一口气,油也就晃动一下;但对着袅袅炊烟吹一口气,炊烟就会变得一团混乱。
[知乎链接] https://www.zhihu.com/question/29005470/answer/62134671
定律
连续性方程(质量守恒定律)
任取一管段,设两处的面积、流体密度和截面上流体的平均流速分别为A1、ρ1、 \(\tilde{v}1\) 和A2、ρ2、 \(\tilde{v}2\) 。
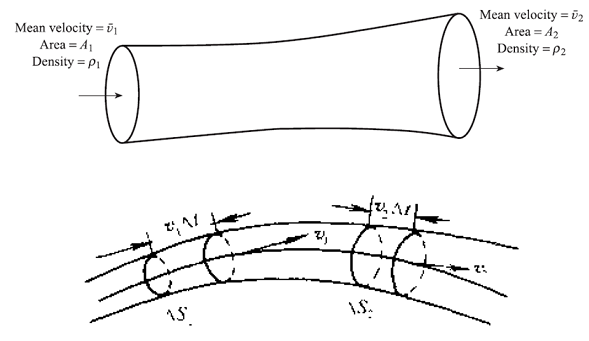
在界面1处的流体质量等于在界面2处的流体质量,即
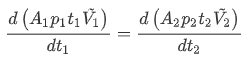
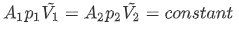
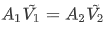
伯努利方程(能量守恒定律)
理想流体在重力场中作稳定流动时,能量守衡定律在流动液体中的表现形式。
稳定流动的理想流体中,忽略流体的粘滞性,任意细流管中的流体满足能量守恒和功能原理。
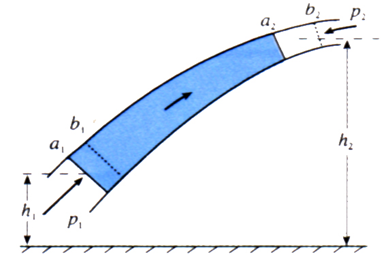
设:流体密度ρ,细流管中分析一段流体a1 a2 :
a1处:S1,v1,h1, p1
a2处:S2,v2,h2, p2
经过微小时间t后,流体a1 a2 移到了b1 b2, 从整体效果看,相当于
将流体 a1 b1 移到了a2 b2, 设a1 b1段流体的质量为m,根据机械能=动能+势能,则:
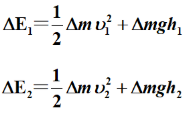
机械能的增量:
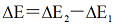
根据压强公式P=F(压力)/S(压力作用面积),做功公式 W=F(压力)·x(流体流动位移)
所以可以算出压强做功:

机械能变化量就是压强所做的功,可得:
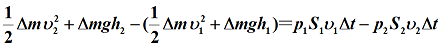
将质量用体积*密度表示

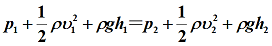
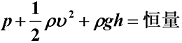
如果理想流体做水平运动,势能一项可以省略
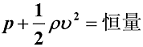
我们也可以看出,在水平流动的流体中,流速大的地方压强小;流速小的地方压强大。
适用性:
伯努利方程,是理想流体作稳定流动时的基本方程,对于实际流体,如果粘滞性很小,如:水、空气、酒精等,可应用伯努利方程解决实际问题。如果实际流体粘滞性不可忽略,在流动过程中要克服流体与管壁以及流体内部的相互摩擦阻力而作功,这将使流体的一部分机械能转化为热能而耗散,机械能不守恒,需要加上损失项才能让等式成立。

