傅里叶变换及其应用一.预备知识
这份随笔是本人对B站斯坦福大学公开课:傅里叶变换及其应用 的学习笔记。
原课程网站:https://see.stanford.edu/Course/EE261
「前言」
这门课不是专门讲定理的,但公式的推导有时候几乎等同于这个公式本身,所以我们需要了解公式推导过程,得以让我们能够利用它,用在不同的情况。傅里叶变换能应用在不同行业中,但由于专业原因,笔记会着着重电子电气的应用。
「课程主线」
课程主线将从傅里叶级数开始,过渡到傅里叶变换。
傅里叶级数的学习,几乎等同于周期性现象做数学上的分析。傅里叶变换可以看成是傅里叶级数的极限形式。它是对非周期现象做数学上的分析。从傅里叶级数开始能明白知识点的链接,一些概念两者是通用的,而一些不是。
「研究的问题」
我们要研究的问题有两个方面,有分析的问题,也有合成的问题。
- 分析:把一个复杂信号或函数分解成一系列简单的组成成分。
- 合成:就是把这些基本的成分重组成一个(新)信号或函数。
分析和合成是成对出现的。不能只考虑其中的一个。而分析和合成是由线性运算完成的,它包含序列和积分。
「周期性现象」
周期性现象可以分为时间域和空间域上的周期性。
- 时间上的周期性,经常用“频率(frequency)”来描述,表示在一秒或一段时间内重复的次数。着重于了解要研究物理量在特定一段时间内的重复次数。
- 空间上的周期性,则使用“周期(period)”来描述,表示在重复的物理量的大小。比如一个重复的图像有多大,着重于了解要研究物理量的大小。
两者的不同源于两者研究的是不同类型的问题。
这两个概念有时候是同时出现,同时共存的。比如一个定期出现的波动,它包含波长(λ)与频率(ϑ)属性。
波长(wavelength)是指波在一个振动周期内传播的距离。也就是沿着波的传播方向,相邻两个振动位相相差2π的点之间的距离。

频率和波长的关系由速度决定,其实就是我们熟悉的,距离=速度*时间。频率和波长存在这样的关系:
λ=V/ϑ
它说明了频率和波长这两个量之间的反比例关系,反比例系数就是速度。这很有趣,它将时间域和空间域联系了起来,在傅里叶变换中,这种反比例关系很常见,无论是时间域和空间域,还是时域与频域。
「对周期性现象建模」
我们可以使用 sin, cos 等这种简单的周期性数学函数,对周期性现象进行建模。
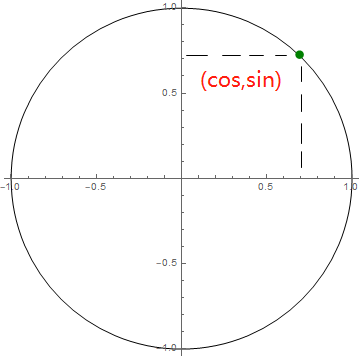
cos(T) , sin(T) 都是以 2π 为最小正周期的函数。他们具有空间上的周期性,即圆上某点(cos,sin)经过 2nπ 后,又会回到原点,所以我们可以用他们来进行建模。
- cos(T+2nπ)=cos(T)
- sin(T+2nπ)=sin(T)
n=0,±1,±2,……(n可以是任意整数)

