luogu P2243 电路维修
P2243 电路维修
题目背景
Elf 是来自Gliese 星球的少女,由于偶然的原因漂流到了地球上。在她无依无靠的时候,善良的运输队员Mark 和James 收留了她。Elf 很感谢Mark和James,可是一直也没能给他们帮上什么忙。
题目描述
有一天 Mark 和James 的飞行车没有办法启动了,经过检查发现原来是电路板的故障。飞行车的电路板设计很奇葩,如下图所示:
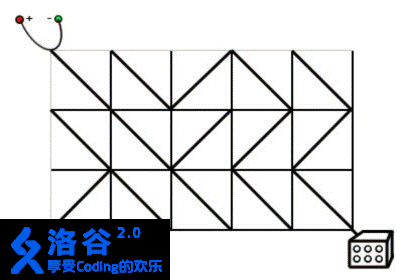
输入输出格式
输入格式:
输入文件包含多组测试数据。第一行包含一个整数T 表示测试数据的数目。
对于每组测试数据,第一行包含正整数 R 和C,表示电路板的行数和列数。
之后 R 行,每行C 个字符,字符是"/"和"\"中的一个,表示标准件的方向。
对于40% 的数据,R,C≤5。
对于 100% 的数据,R,C≤500,T≤5。
输出格式:
对于每组测试数据,在单独的一行输出一个正整数,表示所需的缩小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通,输出 NO SOLUTION。
输入输出样例
输入样例#1:
1 3 5 \\/\\ \\/// /\\\\
输出样例#1:
1
说明
样例的输入对应于题目描述中的情况。
只需要按照下面的方式旋转标准件,就可以使得电源和发动机之间连通。
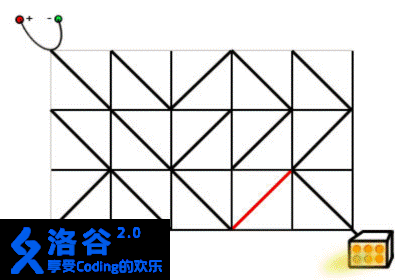
s酱被这题气炸了于是不写了OwO
这个题思路很神奇啊……一开始毫无思路,打开标签,“最短路”,秒懂qwq
把格子的每个交点看做一个点(用s的话说,分配一个新id)
首先看行列点的个数,一奇一偶肯定是NO SOLUTION啦(证明?黑白染色)
然后花式建边:
遇到一个‘/’,就把右上的点和左下的点连一条边权为0的边(可以直接走),同时把左上的点和右下的点连一条边权为1的边(需要改变一条边),‘\’同理
建完边后跑一遍最短路就可以啦
……跑floyd是会T没错啦,但是为什么跑spfa也会迷之TLE啊?
最后还是写了一个堆优化dijkstra才卡过的……

#include<iostream> #include<cstdio> #include<queue> #include<vector> #include<cstring> using namespace std; const int N=300000; int t,r,c,n; int dis[N],p[N],cnt; bool vis[N]; char a[N]; struct node{ int num,dis; bool operator < (node x) const {return dis>x.dis;} }cur; priority_queue<node>q; struct edge{int to,nex,val;}e[N<<2]; inline void add(int u,int v,int w) { e[++cnt]=(edge){v,p[u],w}; p[u]=cnt; } inline void dijk() { memset(dis,0x3f,sizeof(dis));dis[1]=0; while(!q.empty())q.pop(); q.push((node){1,0}); while(!q.empty()) { cur=q.top();q.pop(); if(cur.dis!=dis[cur.num])continue; int u=cur.num; for(int k=p[u];k;k=e[k].nex) { int v=e[k].to; if(cur.dis+e[k].val<dis[v]){ dis[v]=cur.dis+e[k].val; q.push((node){v,dis[v]}); } } if(dis[n]==0)break; } } int main() { scanf("%d",&t); while(t--) { memset(p,0,sizeof(p));cnt=0; scanf("%d%d",&r,&c); bool flag=0; if( (r&1) ^ (c&1) )flag=1; for(int i=1;i<=r;++i) { scanf("%s",a);cin.get(); if(flag)continue; for(int j=1;j<=c;++j) { char ch=a[j-1]; int pos1=i*(c+1)+j,pos2=(i-1)*(c+1)+j; if(ch=='/'){ add(pos1,pos2+1,0);add(pos2+1,pos1,0); add(pos2,pos1+1,1);add(pos1+1,pos2,1); } else{ add(pos1,pos2+1,1);add(pos2+1,pos1,1); add(pos2,pos1+1,0);add(pos1+1,pos2,0); } } } if(flag){cout<<"NO SOLUTION"<<endl;continue;} n=(r+1)*(c+1); dijk(); cout<<dis[n]<<endl; } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号