稀疏正定矩阵的Cholesky分解
稀疏正定矩阵的Cholesky分解
本文大部分参考这篇文章。图片也是从他那里复制的>_<
图和矩阵的对应
考虑矩阵A,如果A[i][j]=w,那么在i,j之间就有一条长度为w的路径。由于我们考虑的是无向图,因此这个矩阵A一定满足\(A=A^T\)
正定(SPD)矩阵的Cholesky分解
要做的事情是将一个正定矩阵A分解为一个下三角矩阵L和其转置的乘积,也即\(A=LL^T\)。
考虑这样一个做法:
for i=1 to n-1
A[i][i]=sqrt(A[i][i])
A[i+1:n][i]=A[i+1:n][i]/A[i][i]
A[i+1:n][i+1:n]=A[i+1:n][i+1:n]-A[i+1:n][i]*(A[i+1:n][i])^T
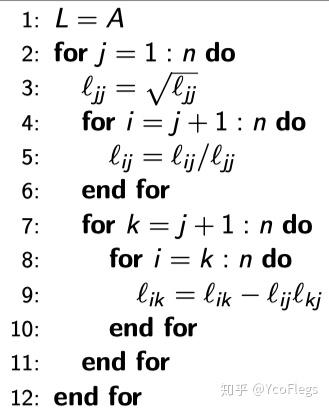
考虑最后那一步,相当于一个矩阵减去一个稀疏向量和其自己转置的外积。
举例说明: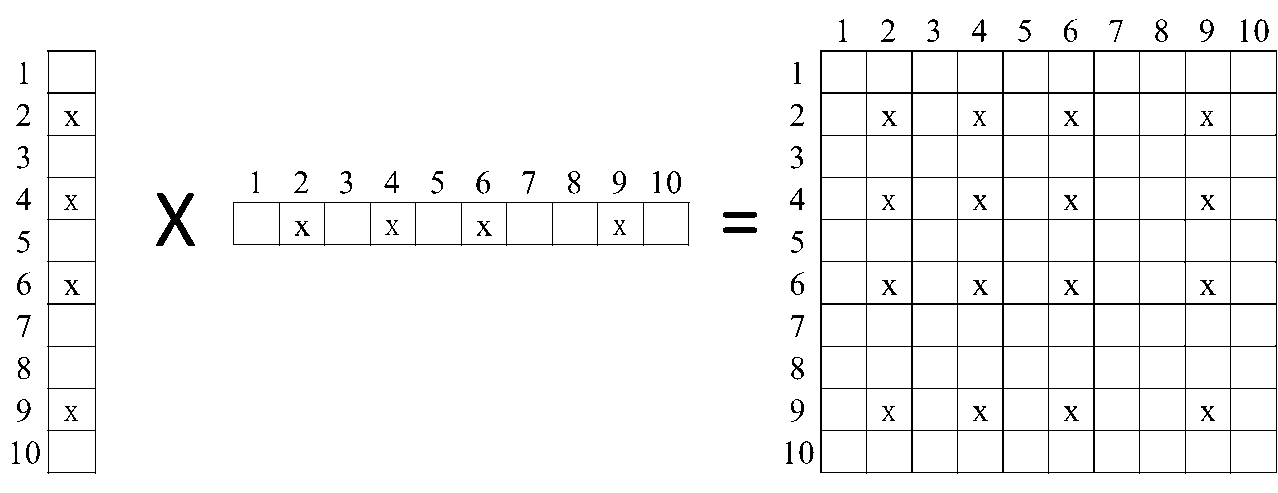
可以发现得到的矩阵一定包含一个稠密子矩阵。
不难知道,如果我们单独取出这个稠密子矩阵,其对应的图一定是一个团。
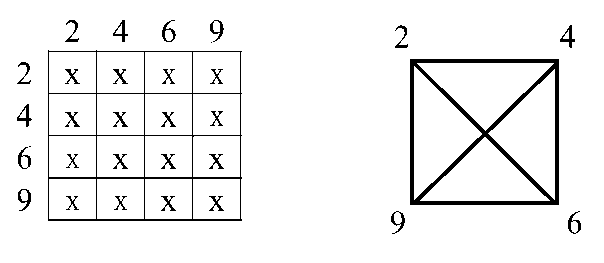
于是这份代码的最后一个步骤可以理解为:我们将第i个节点删去,同时向第i个节点所有连接的节点加边,使他们成为一个团。
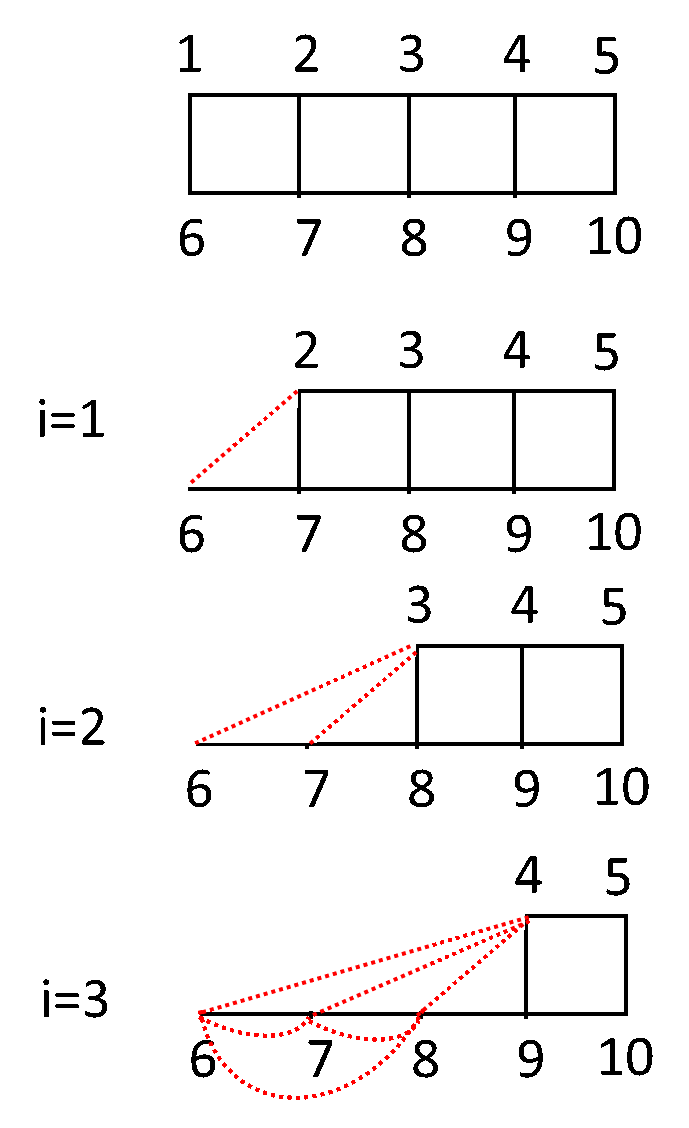
这样子我们就可以得到\(L+L^T\)的所有非零元素的位置。
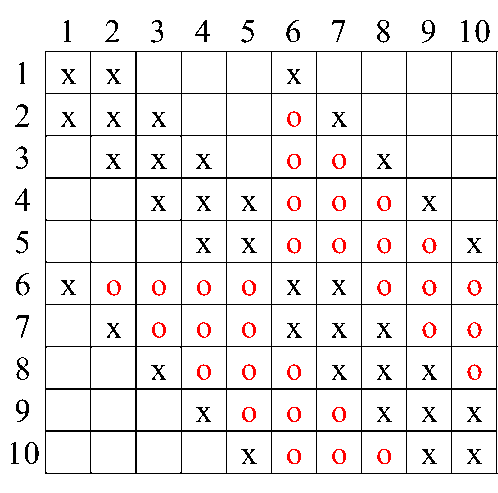
我们通过这样一个方法,可以将正定矩阵的Cholesky分解与图联系起来。
由于最终我们要解决的是稀疏矩阵上的问题,因此我们希望对消去节点的顺序排序,使得最终新增的节点数量最少。但是很可惜,找到最优解已经被证明是一个NP-hard问题。所以我们希望能够得到一个相对来说比较优秀的顺序。
先来看一个3X3分块矩阵的Cholesky分解。
其中D,S,M都可能是稠密的,而L是下三角矩阵。
如果我们最后才把S对应的行和列处理掉(也就是上面的那个沿着对角线依次处理的算法,由于矩阵可以通过行列变换自由交换,故我们这么做是可行的),那么优先处理的部分就是D1,D2,这两个矩阵构成了一个对角矩阵。按照图的说法来讨论的话,S对应着图中的一组节点,我们称之为separator,即一个分段点,先不考虑S,而如果不通过S的话,D1与D2之间没有连边,因此在处理S之前两部分是独立的,此时我们只需要递归的处理D1和D2两部分即可。一个好的separator应当使得最终D1与D2的规模尽可能的一致,并且S中包含的点数尽可能的少。这个方法称之为Nested Dissection。
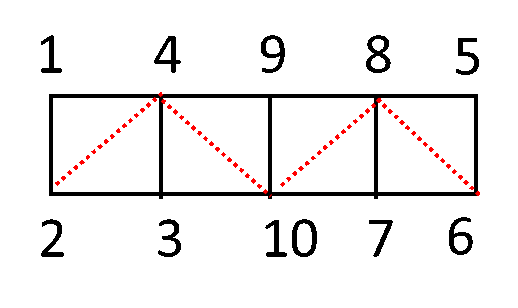
举个栗子,还是前面那张图,我们对其重新进行一个顺序的划分。

于是先处理D1,再处理D2,最后再处理S,这样子最终得到的图就是,红色是新加入的边:
对应到矩阵上,首先通过重新排列行列得到:
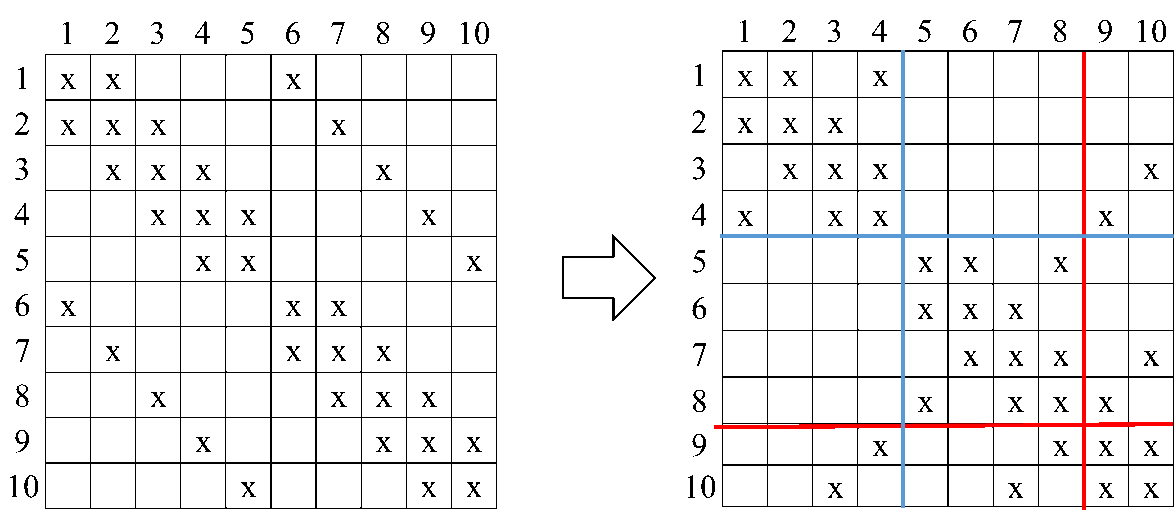
而计算完成之后,得到的\(L+L^T\)为:
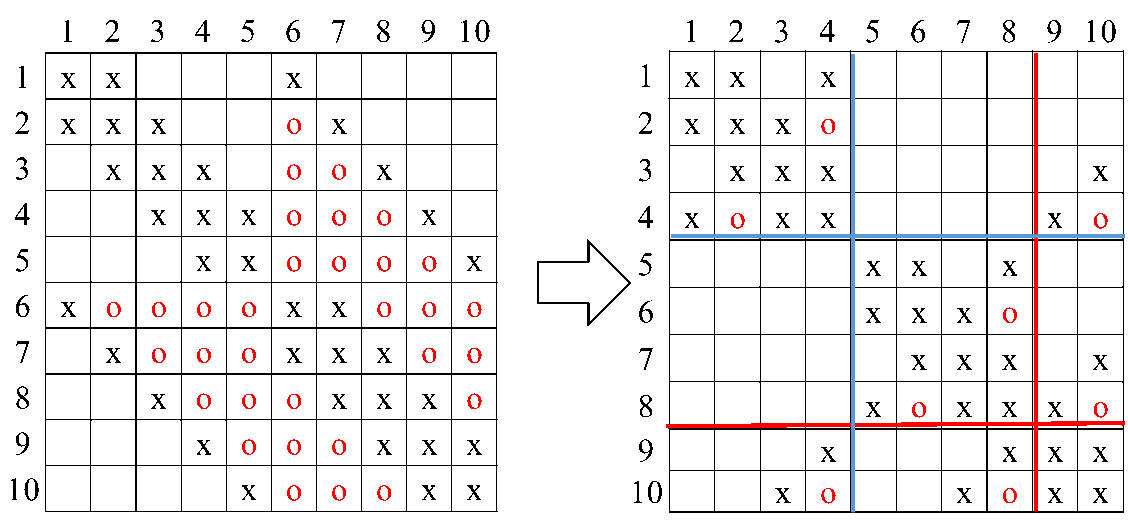
可见,通过这样的优化,我们在矩阵中新加入点的个数减少了。
上面的所有过程都是在无向图中进行考虑的,现在考虑给边定向,我们强制从较大编号的节点指向到较小编号的节点,不难发现这样子这样图一定是一个DAG,这一点和我们在前面的算法中沿着矩阵的行从小往大依次消去是一致的。
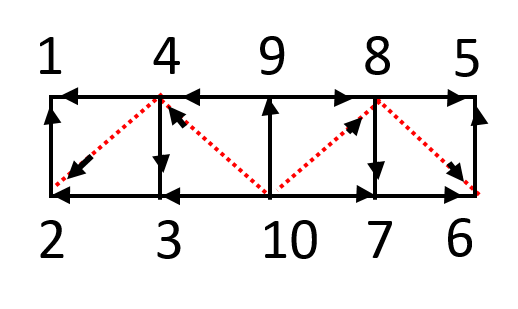
图中的一条边表示了一个依赖关系,也就是如果我们要对于矩阵进行分解,那么如果(i,j)之间存在一条i->j的边,意味着如果我们要计算在矩阵中消去i,我们必须先消去j。我们对其进行拓扑排序,不难发现由于图联通,且我们的图一定是弦图,因此最终得到的一定是一棵树。这棵树被称作elimination tree,也即消去树。
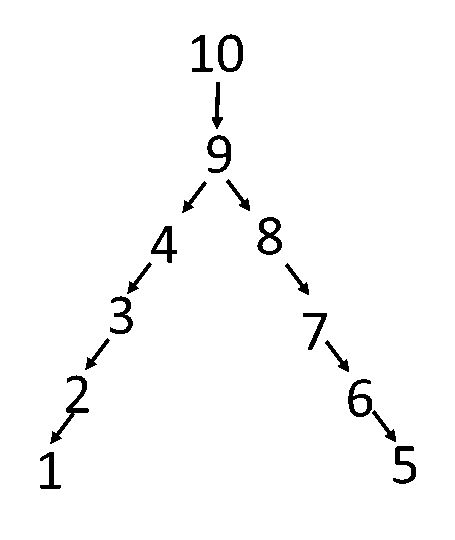
接下来我们以一个例子来介绍Multifrontal方法。
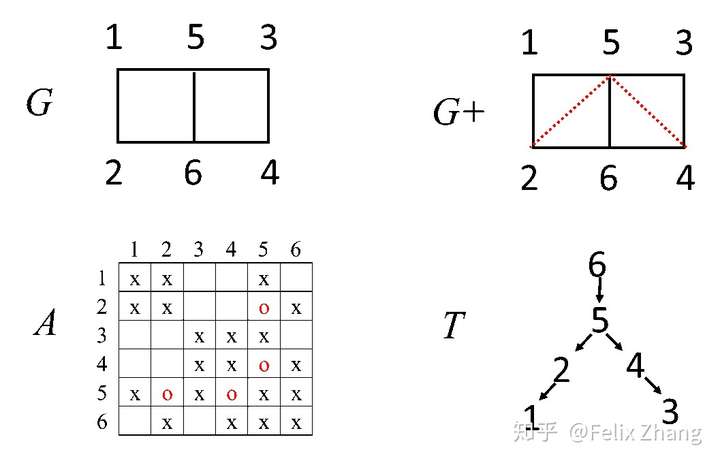
这是一个较为简单的图,G+是其通过前面介绍的算法添加新边之后得到的弦图。A对应着G,其中红色点对应着G+中新加入的边,也就是L相比于A多出的元素。T是其消去树。
我们考虑在消去树T中找到一些稀疏结构“相同”的节点。如果一个子节点在L的列中除了其本身之外和父亲节点有相同的非零元素,那么这两个节点就可以合并。如上面消去树T中的节点5和6。
执行完这个合并步骤之后,我们得到这样一棵树T'
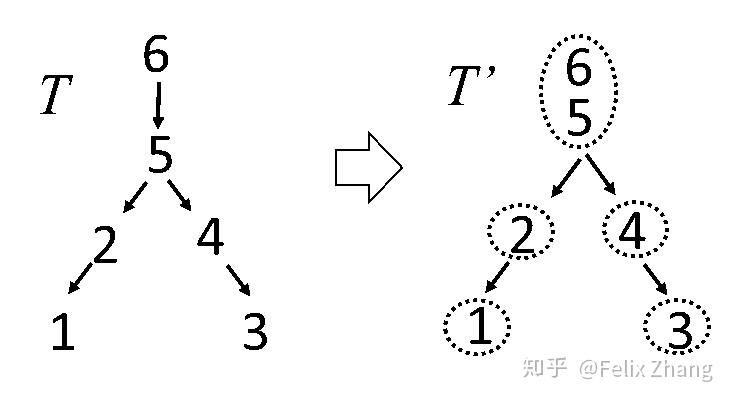
我们称T'为Assembly Tree即,组装树。由于一个组中的节点具有类似的非零元素,故他们组合在一起代表着一个稠密的子矩阵。
假设在T'中的元素i'包含了T中的点集\(M=\{i,j,k...\}\)构成,则在T'中的节点i'对应的子矩阵是M中所有元素值在L(注意是L,它是一个下三角矩阵)中的所有非零元构成。比如果T'中的2',其对应的\(M=\{2\}\),因此其列上的非零元素包含了节点{2,5,6}。因此其对应的子矩阵就是由这几个点构成的3X3矩阵。
在此之前,我们先考虑一个分解问题,我们先考虑一个2X2的分块矩阵的Cholesky分解
于是有\(L_{MM}L_{MM}^T=A_{MM}\),是子矩阵\(A_{MM}\)的Cholesky分解,\(L_{NM}=L_{MM}^{-1}A_{NM}\)是矩阵分解之后产生的一些中间元素。
重点考虑\(L_{NN}L_{NN}^T=A_{NN}-L_{NM}L_{NM}^T\),这里可以类比前面过程中,矩阵减去当前行下方的向量的转置这个过程。
于是,受到这个过程的启发,我们按照顺序来分解矩阵(顺序即从叶子往根节点进行,这与我们消去树中的依赖关系是一致的)。
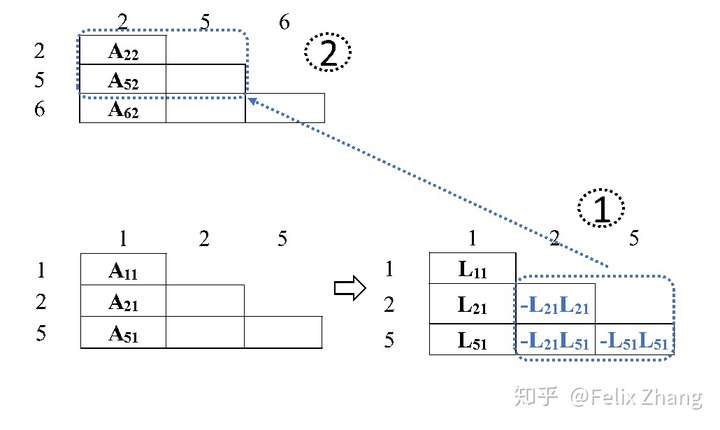
上图为消去1'节点的举例。首先我们提出其对应的矩阵,然后加上其子节点传来的矩阵元素(这里子节点,所以没有这一步),然后直接计算求解这一个小矩阵的Cholesky分解。这一部分也就是前面的\(A_{MM}\)。接着计算\(L_{NM}=L^{-1}_{MM}A_{NM}\),最后计算\(A_{NN}-L_{NM}L_{NM^T}\)传递至父亲节点。
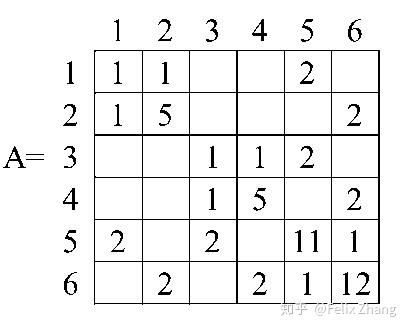
例如我们给出\(A\),这个对应的图就是前面的例子。
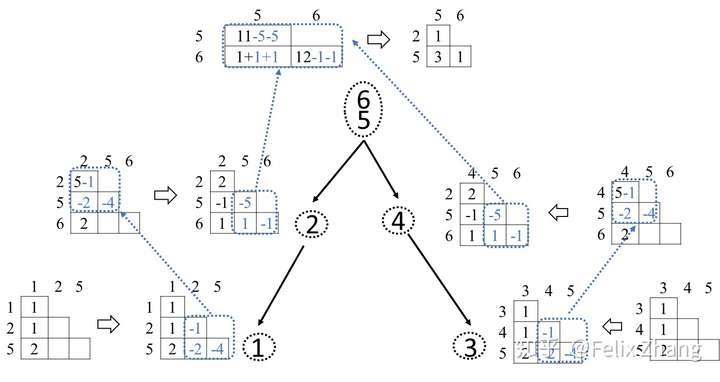
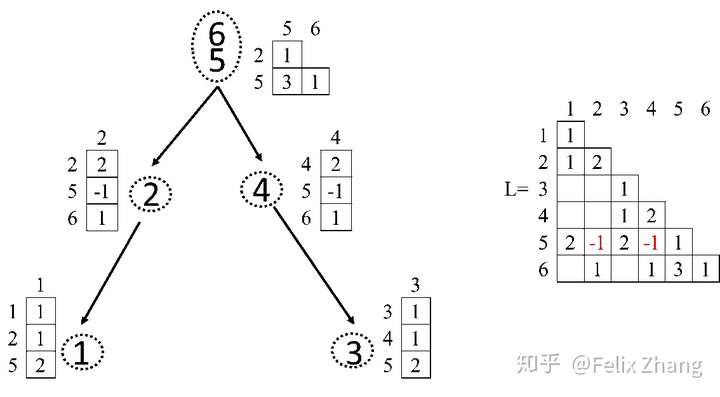
显而易见的,对于不同的分支,其计算在达到LCA之前都是独立的,故所有的未合并且无依赖关系的分支都可以进行并行计算。

