顺序查找算法（二分法）分析及代码示例

　　在工业控制中，二分法算是比较常用的顺序查找算法之一，尤其是在数据量较大的情况下，二分法的算法优势明显。以下将从几个方面来介绍二分法的特点。

---

 一、二分法简介

　　1.1 特点

•  二分法是针对线性数组查找的算法；
•  如果查找的数组是非线性，需要将数组排序，才能使用二分法；
•  相对于轮询查找，二分法算法复杂度低；
• 二分法每次将数据范围缩小为上次的一半；

　　1.2、原理

　　　　二分法根据数组递增和递减的不同，二分法实现算法有所不同。

　　　　二分法初始front为查询范围最前面的数据，初始end为查询范围最后面的数据，mid一直为查询范围中间的数据。

 

 

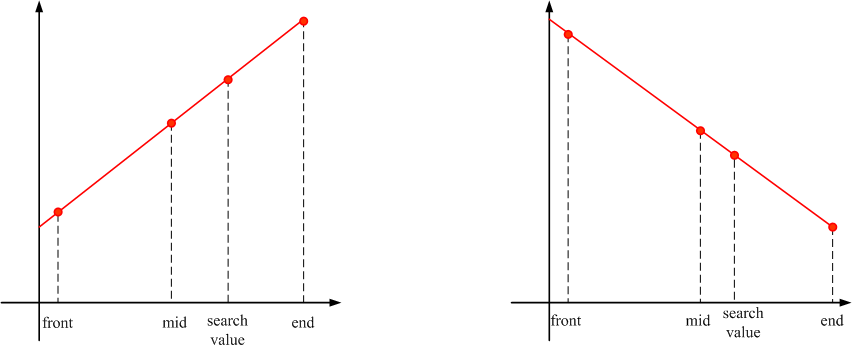
　　　　对于递增的数列，如果search value  > arrayup[mid],将查找的front值更新为mid值，mid值更新为（front+end）/2；

　　　　对于递增的数列，如果search value  < arrayup[mid],将查找的end值更新为mid值，mid值更新为（front+end）/2；

　　　　对于递减的数列，如果search value  > arraydown[mid],将查找的end值更新为mid值，mid值更新为（front+end）/2；

　　　　对于递减的数列，如果search value  < arraydown[mid],将查找的front值更新为mid值，mid值更新为（front+end）/2；

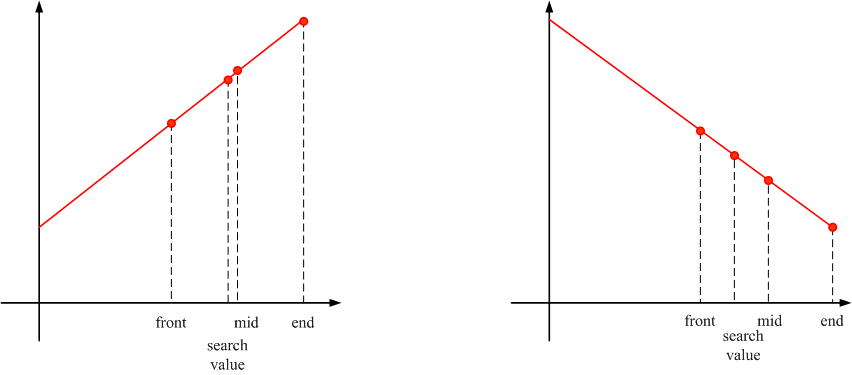
　　由上次可知，每查询一次，查询范围就缩小一半，mid值对于的值就更加接近于search value。

二、二分法代码实现

　　2.1使用for 和 if 逻辑实现

#include <stdio.h>

int main() {
    
    int j = 500;
    int arrup[256],arrdown[256];
    int front,mid,end;
    int search_value = 300;
    
     //Init the array data
    for(int i = 0; i < 256; i++){
        
        arrup[i] = 135 + i;
        arrdown[i] = 500 - i;
    }

    //Init the search range
    front = 0;
    end = 256;
    mid = (front + end)>>1;
    
    //for step up array,shrink the search range algorithm
    for( int i = 0; i < 5; i++){
        if(search_value > arrup[mid]){
            front = mid;
            mid = (front + end)>>1;
            printf("The end is %d,The mid is %d,The min is %d\n",end,mid,front);
            
        }else if(search_value < arrup[mid]){
            
            end = mid;
            mid = (front + end)>>1;
            printf("The end is %d,The mid is %d,The front is %d\n",end,mid,front);
            
        }
    }
    
    printf("\n\n\n");
    
    //Init the array data
    front = 0;
    end = 256;
    mid = (front + end)>>1;
    
    //for step down array,shrink the search range algorithm
    for( int i = 0; i < 5; i++){
        if(search_value > arrdown[mid]){
            end = mid;
            mid = (front + end)>>1;
            printf("The end is %d,The mid is %d,The min is %d\n",end,mid,front);
            
        }else if(search_value < arrdown[mid]){
            
            front = mid;
            mid = (front + end)>>1;
            printf("The end is %d,The mid is %d,The front is %d\n",end,mid,front);
            
        }
    }
    
    
    return 0;
}

　　代码执行结果为：　　

        The end is 256,The mid is 192,The min is 128
        The end is 192,The mid is 160,The front is 128
　　The end is 192,The mid is 176,The min is 160
　　The end is 176,The mid is 168,The front is 160
　　The end is 168,The mid is 164,The front is 160



　　The end is 256,The mid is 192,The front is 128
　　The end is 256,The mid is 224,The front is 192
　　The end is 224,The mid is 208,The min is 192
　　The end is 208,The mid is 200,The min is 192

　　对于递增数列，arrup[164] = 299,    程序里面的search value为300，误差为1；
　　对于递减数列，arrdown[200] = 300,程序里面的search value为300，误差为0；

　　通过增加查询次数，可以提高查询的精度，减小误差。比如：将上述代码46行的查询次数由5改为7，运行结果如下：

　　The end is 256,The mid is 192,The min is 128
　　The end is 192,The mid is 160,The front is 128
　　The end is 192,The mid is 176,The min is 160
　　The end is 176,The mid is 168,The front is 160
　　The end is 168,The mid is 164,The front is 160
　　The end is 168,The mid is 166,The min is 164
　　The end is 166,The mid is 165,The front is 164

　　对于递增数列，arrup[165] = 300, 程序里面的search value为300，误差为0；

2.2使用while和 if 逻辑实现

#include <stdio.h>

int main() {
    
    int j = 500;
    int arrup[256],arrdown[256];
    int front,mid,end;
    int search_value = 300;
    
     //Init the array data
    for(int i = 0; i < 256; i++){
        
        arrup[i] = 135 + i;
        arrdown[i] = 500 - i;
    }

    //Init the search range
    front = 0;
    end = 256;
    mid = (front + end)>>1;
    
    //for step up array,shrink the search range algorithm
    while(front < end){
       
        if(search_value > arrup[mid]){
            front = mid;
            mid = (front + end)>>1;
        }else if(search_value < arrup[mid]){
            end = mid;
            mid = (front + end)>>1;
        }else{
            break;
        }
        printf("The end is %d,The mid is %d,The front is %d\n",end,mid,front);
    }
    
    printf("\n\n\n");
    
    //Init the array data
    front = 0;
    end = 256;
    mid = (front + end)>>1;
    
    //for step down array,shrink the search range algorithm
    while(front < end){
        
        if(search_value > arrdown[mid]){
            end = mid;
            mid = (front + end)>>1;
        }else if(search_value < arrdown[mid]){
            front = mid;
            mid = (front + end)>>1;
        }else{
            break;
        }
        printf("The end is %d,The mid is %d,The front is %d\n",end,mid,front);
    }
    
    return 0;
}

　　代码执行结果为：

　　The end is 256,The mid is 192,The front is 128
　　The end is 192,The mid is 160,The front is 128
　　The end is 192,The mid is 176,The front is 160
　　The end is 176,The mid is 168,The front is 160
　　The end is 168,The mid is 164,The front is 160
　　The end is 168,The mid is 166,The front is 164
　　The end is 166,The mid is 165,The front is 164


　　The end is 256,The mid is 192,The front is 128
　　The end is 256,The mid is 224,The front is 192
　　The end is 224,The mid is 208,The front is 192
　　The end is 208,The mid is 200,The front is 192

　　对于递增数列，arrup[165] = 299,  程序里面的search value为300，误差为0；
　　对于递减数列，arrdown[200] = 300,程序里面的search value为300，误差为0；

三、总结分析
　　使用for和if的逻辑实现，需要实现设定查询的次数，但是查询次数不够的时候存在误差。
　　使用while和if的逻辑实现，不需要设定查询的次数，精度较高，但是查询次数相对较多。