OI+ACM 笔记：G - 计算几何

G - 计算几何

计算几何基础

精度

误差量：通常来说，若问题要求精确到小数点后 \(\alpha\) 位，则误差量 \(\epsilon = 10^{-(\alpha + 2)}\)。

const double eps = 1e-...;

符号函数：

int sgn(double x) {
	if (fabs(x) < eps) return 0;
	return x > 0 ? 1 : -1;
}

比较函数：

int dcmp(double x, double y) { return sgn(x - y); }

点、向量

点、向量的结构体声明：

struct point {
	double x, y;
    point() { x = y = 0; }
	point(double A, double B) : x(A), y(B) {}
};

typedef point vec;

// vector addition, subtraction and multiplication.
vec operator + (vec a, vec b) { return vec(a.x + b.x, a.y + b.y); }
vec operator - (vec a, vec b) { return vec(a.x - b.x, a.y - b.y); }
vec operator * (vec a, double b) { return vec(a.x * b, a.y * b); }

// dot product.
double dot(vec a, vec b) {
	return a.x * b.x + a.y * b.y;
}

// cross product.
double cross(vec a, vec b) {
	return a.x * b.y - b.x * a.y;
}

// vector length.
double get_length(vec a) { return sqrt(dot(a, a)); }

// vector angle.
double get_angle(vec a, vec b) { return acos(dot(a, b) / get_length(a) / get_length(b)); }

// vector anticlockwise rotate.
vec rotate(vec a, double angle) {
	double x = a.x * cos(angle) - a.y * sin(angle);
	double y = a.x * sin(angle) + a.y * cos(angle);
	return vec(x, y);
}

点积：\(\vec{a}\) 与 \(\vec{b}\) 的点积，为 \(\vec{a}\) 在 \(\vec{b}\) 上的投影与 \(\vec{b}\) 的模长的积，易证该点积也为 \(\vec{b}\) 在 \(\vec{a}\) 上的投影与 \(\vec{a}\) 的模长的积。

\[\begin{aligned} \vec{a} \cdot \vec{b} & = |\vec{a}||\vec{b}| \cos \langle \vec{a}, \vec{b} \rangle \\ & = x_ax_b + y_ay_b \end{aligned} \]

叉积：\(\vec{a}\) 的 \(\vec{b}\) 的叉积，为 \(\vec{a}\) 与 \(\vec{b}\) 围成的平行四边形的有向面积（以 \(\vec{a}\) 为基准，逆时针为正、顺时针为负）。

\[\begin{aligned} \vec{a} \times \vec{b} & = |\vec{a}||\vec{b}| \sin \langle \vec{a}, \vec{b} \rangle \\ & = x_ay_b - y_ax_b \end{aligned} \]

直线

直线表示法：可用一对互不相同的点确定一条直线，也可以用直线上一点和直线上的方向向量确定一条直线。

直线 \(p + x \cdot t\) 与 \(q + y \cdot t\) 求交：

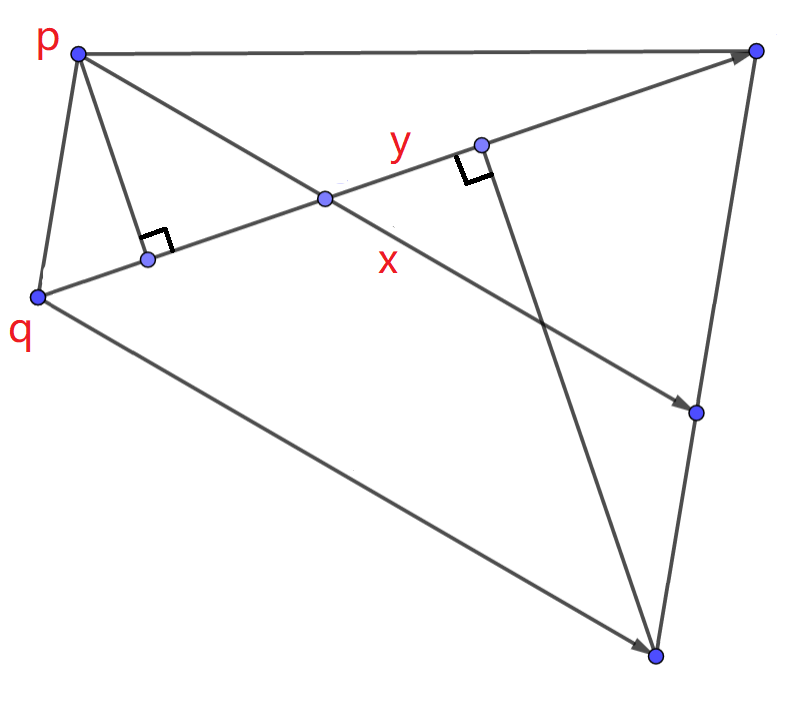
point line_intersection(point p, vec x, point q, vec y) {
	vec u = q - p;
	double t = cross(u, y) / cross(x, y);
	return p + x * t;
}

点 \(p\) 到直线 \(AB\) 的距离：

double distance_line(point p, point a, point b) {
	vec u = b - a, v = p - a;
	return fabs(cross(u, v)) / get_length(u);
}

点 \(p\) 到线段 \(AB\) 的距离：

double distance_seg(point p, point a, point b) {
	if (a == b) return get_length(p - a);
	vec u = b - a, va = p - a, vb = p - b;
	if (sgn(dot(u, va)) < 0) return get_length(va);
	if (sgn(dot(u, vb)) > 0) return get_length(vb);
	return distance_line(p, a, b);
}

点 \(p\) 在直线 \(AB\) 上的投影（垂线段的垂足）：

double line_projection(point p, point a, point b) {
	vec u = b - a, v = p - a;
	return a + u * (dot(u, v) / dot(u, u));
}

点 \(p\) 是否在线段 \(AB\) 上：

bool on_seg(point p, point a, point b) {
	vec u = p - a, v = p - b;
	return !sgn(cross(u, v)) && sgn(dot(u, v)) <= 0;
}

线段 \(AB\) 与 \(CD\) 是否有交点（跨立实验）：

bool seg_intersection(point Xa, point Xb, point Ya, point Yb) {
	int X = 1, Y = 1;
	X *= sgn(cross(Xb - Xa, Ya - Xa));
	X *= sgn(cross(Xb - Xa, Yb - Xa));
	Y *= sgn(cross(Yb - Ya, Xa - Ya));
	Y *= sgn(cross(Yb - Ya, Xb - Ya));
	return X <= 0 && Y <= 0;
}

应用

三角形面积（坐标）：

double area(point a, point b, point c) {
	return fabs(cross(b - a, c - a)) / 2;
}

三角形面积（边长）：

double area(double a, double b, double c) {
	double p = (a + b + c) / 2;
	return sqrt(p * (p - a) * (p - b) * (p - c));
}

多边形面积：不一定要凸多边形，但要保证多边形的顶点按顺时针或逆时针的顺序给出。

double polygon_area(int n, point p[]) {
	double sum = 0;	
	for (int i = 2; i < n; i ++) sum += cross(p[i] - p[1], p[i + 1] - p[i]);
	return fabs(ans / 2);
}

凸包

• 在 \(n \times n\) 的整点网格中，最大凸包的大小为 \(\mathcal{O}(n^{\frac{2}{3}})\) 级别。