【比赛题解】CSP2019 提高组题解
D1T1. 格雷码
Solution
一道简单的分治。
- 1 位格雷码由两个 1 位二进制串组成,顺序为:0,1。
- \(n + 1\) 位格雷码的前 \(2^n\) 个二进制串,可以由依次算法生成的 \(n\) 位格雷码(总共 \(2^n\) 个 \(n\) 位二进制串)按顺序排列,再在每个串前加一个前缀 0 构成。
- \(n + 1\) 位格雷码的后 \(2^n\) 个二进制串,可以由依次算法生成的 \(n\) 位格雷码(总共 \(2^n\) 个 \(n\) 位二进制串)按逆序排列,再在每个串前加一个前缀 1 构成。
通过上面的这段 " 一种格雷码的生成算法 " 我们可以知道,对于任意的 \(n(n \geq 2)\),\(n\) 位格雷码总是可以由 \(n - 1\) 位格雷码加一个前导 0 或前导 1 构成,考虑分治。
记 \(\mathrm{calc}(n, k)\) 表示 \(n\) 位格雷码中的 \(k\) 号二进制串。
首先是递归边界 \(n = 1\),此时若 \(k = 0\),则 \(\mathrm{calc}(n, k) = 0\);若 \(k = 1\),则 \(\mathrm{calc}(n, k) = 1\)。
对于任意的 \(n(n \geq 2)\),此时有两种情况:
- 若 \(k < 2^{n - 1}\),则 \(\mathrm{calc}(n, k) = 0 + \mathrm{calc}(n - 1, k)\)。
- 若 \(k \geq 2^{n - 1}\),则 \(\mathrm{calc}(n, k) = 1 + \mathrm{calc}(n - 1, 2^n - 1 - k)\)。
时间复杂度 \(\mathcal{O(n)}\),记得开 unsigned long long。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
using namespace std;
int n;
unsigned long long k;
string calc(int n, unsigned long long k) {
if (n == 1) return k == 0 ? "0" : "1";
else {
unsigned long long S = 1ull << (n - 1);
if (k < S) return "0" + calc(n - 1, k);
else return "1" + calc(n - 1, S - 1 + S - k);
}
}
int main() {
cin >> n >> k;
cout << calc(n, k) << endl;
return 0;
}
D1T2. 括号树
Solution
注意到答案的形式是 \((1 \times k_1) \ \text{xor} \ (2 \times k_2) \ \text{xor} \ (3 \times k_3) \ \text{xor} \ ⋯ \ \text{xor} \ (n \times k_n)\),这使得我们难以对答案进行一些分析,只能乖乖地把 \(k_1, k_2, k_3, ..., k_n\) 都求出来,再计算出答案。
采用增量法。对树进行 DFS,每次计算以 \(u\) 为最底点的新增答案,将这个量记作 \(\mathrm{cnt}_u\)。
考虑维护一个栈,维护从根到当前节点尚未匹配的左括号编号。
考虑当前节点:
- 如果是左括号,则该括号无法匹配,此时有 \(\mathrm{cnt}_u = 0\),将该点加入栈中,接着搜索即可。
- 如果是右括号,则该括号与栈顶 \(p\) 匹配(若栈为空则无法匹配),此时有 \(\mathrm{cnt}_u = \mathrm{cnt}_{fa_p} + 1\),将栈顶弹出,接着搜索即可。
时间复杂度 \(\mathcal{O}(n)\)。
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long s64;
template <class T>
inline void read(T &x) {
static char s;
while (s = getchar(), s < '0' || s > '9');
x = s - '0';
while (s = getchar(), s >= '0' && s <= '9') x = x * 10 + s - '0';
}
const int N = 500100;
int n;
char s[N];
int Fa[N];
int tot, head[N], ver[N], Next[N];
void add_edge(int u, int v) {
ver[++ tot] = v; Next[tot] = head[u]; head[u] = tot;
}
int top, stk[N];
int cnt[N];
s64 k[N];
void dfs(int u) {
int p = 0;
if (s[u] == '(') stk[++ top] = u;
else if (top) cnt[u] = cnt[Fa[p = stk[top --]]] + 1;
k[u] = k[Fa[u]] + cnt[u];
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
dfs(v);
}
if (s[u] == '(') top --;
else if (p) stk[++ top] = p;
}
int main() {
read(n);
scanf("%s", s + 1);
for (int i = 2; i <= n; i ++)
read(Fa[i]), add_edge(Fa[i], i);
dfs(1);
s64 ans = 0;
for (int i = 1; i <= n; i ++) ans ^= (k[i] * i);
printf("%lld\n", ans);
return 0;
}
D1T3. 树上的数
Solution
咕咕咕。
D2T1. Emiya 家今天的饭
Solution
算法一
在不考虑每种主要食材至多在一半的菜中被使用时,答案即为:
我们可以简单容斥一下,先求出在 " 存在一种主要食材使用次数大于菜的一半 " 情况下的方案数,再与上式做个差即可求出答案。
注意到有且仅有一种主要食材使用次数大于菜的一半,我们可以枚举这个主要食材,记我们枚举的主要食材的编号为 \(col\),对于每一个主要食材,考虑 dp。
设 \(f(i, j, k)\) 表示:在前 \(i\) 个烹饪方法中,做了 \(j\) 道菜,且第 \(col\) 种主要食材用了 \(k\) 个时的方案数。
设 \(S_i = \sum_{1 \leq j \leq m} a_{i, j}\),转移有三种:
- 不使用第 \(i\) 个烹饪方法做菜。
- 使用第 \(i\) 个烹饪方法做菜,使用第 \(col\) 种主要食材。
- 使用第 \(i\) 个烹饪方法做菜,不使用第 \(col\) 种主要食材。
故有状态转移方程:
答案即为 \(\sum\limits_{j = 1}^n\sum\limits_{k = \left\lfloor\frac{j}{2}\right\rfloor + 1}^j f(n, j, k)\)。
直接做 dp 的时间复杂度 \(\mathcal{O}(n^3m)\)。
算法二
考虑维度合并,注意到我们只关心 \(\left\lfloor\frac{j}{2}\right\rfloor\) 与 \(k\) 的差值,并不关心 \(j\) 与 \(k\) 的值具体是多少,于是我们可以将 \(j\) 这一维和 \(k\) 这一维进行合并。
设 \(f(i, j)\) 表示:在前 \(i\) 个烹饪方法中," 使用第 \(col\) 种主要食材做的菜数 " 减去 " 不使用第 \(col\) 种主要食材做的菜数 " 的差值为 \(j\) 时的方案数。
转移依旧是上述的三种。简单分析即可得到状态转移方程:
答案即为 \(\sum\limits_{j = 1}^n f(n, j)\)。
时间复杂度 \(\mathcal{O}(n^2 m)\)。
注意到差值 \(j\) 也有可能是负数,所以我们需要用一个偏移量 \(\text{base}\),使得值域变为非负整数域后再进行处理。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read() {
int x = 0, f = 1; char s = getchar();
while (s < '0' || s > '9') { if (s == '-') f = -f; s = getchar(); }
while (s >= '0' && s <= '9') { x = x * 10 + s - '0'; s = getchar(); }
return x * f;
}
const int N = 110, M = 2010, base = 100;
const int mod = 998244353;
int n, m;
int a[N][M];
int S[N];
int f[N][N * 2];
int main() {
n = read(), m = read();
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
a[i][j] = read();
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
S[i] = (S[i] + a[i][j]) % mod;
int ans = 1;
for (int i = 1; i <= n; i ++)
ans = 1ll * ans * (S[i] + 1) % mod;
ans = ((ans - 1) % mod + mod) % mod;
for (int col = 1; col <= m; col ++) {
memset(f, 0, sizeof(f));
f[0][0 + base] = 1;
for (int i = 1; i <= n; i ++)
for (int j = -i + base; j <= i + base; j ++) {
int val = 0;
val = (val + f[i - 1][j]) % mod;
if (j) val = (val + 1ll * f[i - 1][j - 1] * a[i][col]) % mod;
val = (val + 1ll * f[i - 1][j + 1] * (S[i] - a[i][col])) % mod;
val = (val % mod + mod) % mod;
f[i][j] = val;
}
for (int j = 1 + base; j <= n + base; j ++)
ans = ((ans - f[n][j]) % mod + mod) % mod;
}
printf("%d\n", ans);
return 0;
}
D2T2. 划分
Solution
考虑 dp,记 \(S_i = \sum_{1 \leq j \leq i} a_j\)。
设 \(f(i, j)\) 表示:考虑到前 \(i\) 项,划分的最后一段区间为 \((j, i]\) 时,能取得的最小的平方和。
显然有状态转移方程:
直接做的时间复杂度为 \(\mathcal{O}(n^3)\)。
引理
定义,当决策点 \(k\) 若满足 \(S_j - S_k \leq S_i - S_j\),则被称为 " 合法 "。
对于合法的两个决策点 \(k_1, k_2\),不妨设 \(k_1 < k_2\),则决策点 \(k_2\) 不劣于 \(k_1\)。
根据引理可知,在合法范围内,\(f(i, j)\) 随 \(j\) 单调递减。也就是说,当最后若干段尽量小时,能取得的平方和会尽量小。
于是我们大力 dp。设 \(f(i)\) 表示考虑到前 \(i\) 项时,能取得的最小的平方和;\(p_i\) 表示 \(f(i)\) 的最优决策点;\(\mathrm{suf}_i\) 表示 \(f(i)\) 中最后一段划分的区间和,其实就是 \(S_i - S_{p_i}\)。
显然有状态转移方程:
我们重新定义,当决策点 \(j\) 若满足 \(\mathrm{suf}_j \leq S_i - S_j\) ,则被称为 " 合法 ",移项得 \(\mathrm{suf}_j + S_j \leq S_i\)。
注意到 \(\mathrm{suf}_j + S_j \leq S_i\) 中的 \(S_i\) 是单调递增的,说明决策集合只增大不减小。于是只需要记一个最靠右的合法决策,单调队列维护待加入的决策即可。
一看就是要打高精(还要压位),时空复杂度都比较紧张。在转移的时候,并不用事先计算出 dp 值 \(f(i)\),只需记录 \(f(i)\) 的最优决策点 \(p_i\),最后从 \(n\) 倒推回去并计算答案即可。
时间复杂度 \(\mathcal{O(n)}\)。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read() {
int x = 0, f = 1; char s = getchar();
while (s < '0' || s > '9') { if (s == '-') f = -f; s = getchar(); }
while (s >= '0' && s <= '9') { x = x * 10 + s - '0'; s = getchar(); }
return x * f;
}
inline void print(__int128 x) {
if (x > 9) print(x / 10);
putchar('0' + x % 10);
}
const int N = 40001000, M = 100100;
int n, type;
int a[N];
void makedata() {
static int x, y, z, b[N], m, p[M], l[M], r[M], mod = (1 << 30);
x = read(), y = read(), z = read(), b[1] = read(), b[2] = read(), m = read();
p[0] = 0;
for (int i = 1; i <= m; i ++)
p[i] = read(), l[i] = read(), r[i] = read();
for (int i = 3; i <= n; i ++)
b[i] = (1ll * x * b[i - 1] + 1ll * y * b[i - 2] + z) % mod;
for (int j = 1; j <= m; j ++)
for (int i = p[j - 1] + 1; i <= p[j]; i ++)
a[i] = (b[i] % (r[j] - l[j] + 1)) + l[j];
}
long long S[N];
int l, r;
int q[N];
int dec[N];
long long suf(int x) {
return S[x] - S[dec[x]];
}
int main() {
n = read(), type = read();
if (type == 1) makedata();
else
for (int i = 1; i <= n; i ++)
a[i] = read();
for (int i = 1; i <= n; i ++)
S[i] = S[i - 1] + a[i];
l = 1, r = 1;
q[1] = 0;
int p = 0;
for (int i = 1; i <= n; i ++) {
while (l <= r && S[q[l]] + suf(q[l]) <= S[i]) p = max(p, q[l ++]);
dec[i] = p;
while (l <= r && S[q[r]] + suf(q[r]) >= S[i] + suf(i)) r --;
q[++ r] = i;
}
__int128 ans = 0;
int x = n;
while (x) {
ans += (__int128) suf(x) * suf(x);
x = dec[x];
}
print(ans);
return 0;
}
D2T3. 树的重心
Solution
Test 12 - 15
部分分:树的形态为满二叉树。
当树的形态为满二叉树的时候,删掉一条边 \((u, v)\),不妨设 \(u\) 是 \(v\) 的父亲。
\(v\) 的子树内的重心还是很好分析的,显然 \(v\) 的子树也是满二叉树,故重心即为 \(v\)。
考虑在原树中刨去 \(v\) 的子树后,重心的分布。不妨设树的深度为 \(d\)。
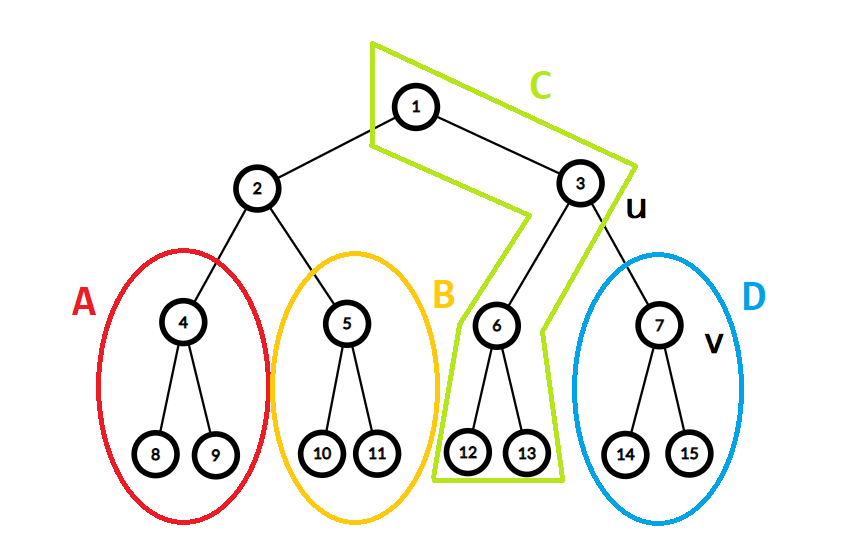
上图是一棵满二叉树,我们先对 \((u, v)\) 在满二叉树的右侧时讨论,左侧同理。我们把树分成了四个部分和一个点,设 \(v\) 的深度为 \(p\),则各个部分的节点数为:
- \(\color{red}A \color{black}: 2^{d-2} - 1\)。
- \(\color{yellow}B \color{black}: 2^{d-2} - 1\)。
- \(\color{green}C \color{black}: 2^{d - 1} - 2^{d - p + 1} + 1\)。
- \(\color{blue}D \color{black}: 2^{d - p + 1} - 1\)。
首先,重心显然不会出现在 \(\color{red}A\) 和 \(\color{yellow}B\) 里,也并不可能出现在 \(\color{green}C\) 中除了根节点以外的节点中。
我们对 \(2\) 号点(根的其中一个儿子)与根节点进行重点讨论:
- 删除 \(2\) 号点后剩下的最大子树:\(x = \max(2^{d - 2} - 1, 2^{d - 1} - 2^{d - p + 1} + 1)\)。
- 删除根节点后剩下的最大子树:\(y = \max(2^{d - 1} - 1, 2^{d - 1} - 2^{d - p + 1})\)。
当 \(p < d\) 时,有 \(x < 2^{d - 1} - 1\),\(y = 2^{d - 1} - 1\)。\(x < y\),此时 \(2\) 号点是重心。
当 \(p = d\) 时,有 \(x = 2^{d - 1} - 1\),\(y = 2^{d - 1} - 1\)。\(x = y\),此时 \(2\) 号点与根节点都是重心。
设根节点为 \(a\),根节点的左儿子为 \(b\),根节点的右儿子为 \(c\)。我们发现,当 \((u, v)\) 在满二叉树的右侧时,这条边对答案有 \(b\) 的贡献,当 \((u, v)\) 在满二叉树的左侧时,这条边对答案有 \(c\) 的贡献,特别地,当 \((u, v)\) 中的 \(v\) 为叶节点时,这条边对答案还有额外的 \(a\) 的贡献。
经过上述分析,故答案为:
正解
不难想到,可以对于每个点 \(u\),计算 \(u\) 成为重心时,对答案的贡献。
我们钦定点 \(u\) 为整棵树的根,现在有一个 \(u\) 的子节点 \(v\),我们要从 \(v\) 的子树中再删去一个小子树,使得 \(u\) 成为重心。设选出的子树大小为 \(s_0\),\(v\) 的子树原大小为 \(s_v\),\(m\) 为 \(u\) 除了 \(v\) 以外子树的最大子树大小。
由于 \(u\) 为重心的充要条件为 \(u\) 的最大子树大小不超过整棵树的一半。故:
(1):\(v\) 的新子树大小不能超过总体的 \(\frac{1}{2}\)
(2):除 \(v\) 之外的最大子树大小不能超过总体的 \(\frac{1}{2}\)
综合一下可以得到:
于是问题转化为 \(v\) 的子树内有多少个点的子树大小在某个区间范围内,线段树合并直接可以 rush 掉。
但是显然不能每次都以 \(u\) 为根重新做一遍线段树合并,我们钦定 \(1\) 为整棵树的根。
若 \(v\) 是 \(u\) 的子节点,我们可以线段树合并简单统计一下。若 \(v\) 是 \(u\) 的父亲节点时,可以根据其是否处于 \(1\) 至 \(u\) 的路径上分类讨论。
时空复杂度 \(\mathcal{O(n \log n)}\)。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read() {
int x = 0, f = 1; char s = getchar();
while (s < '0' || s > '9') { if (s == '-') f = -f; s = getchar(); }
while (s >= '0' && s <= '9') { x = x * 10 + s - '0'; s = getchar(); }
return x * f;
}
const int N = 300100, M = 600100, MLOGN = 10000000;
int n;
int ovo, head[N], ver[M], Next[M];
void addedge(int u, int v) {
ver[++ ovo] = v; Next[ovo] = head[u]; head[u] = ovo;
}
// BIT part
int c[N];
void add(int x, int val) {
for (; x <= n; x += x & -x) c[x] += val;
}
int calc(int x) {
int ans = 0;
for (; x; x -= x & -x) ans += c[x];
return ans;
}
// SegmentTree part
int tot, root[N];
struct SegmentTree {
int lc, rc;
int cnt;
} t[MLOGN];
int New() {
tot ++;
t[tot].lc = t[tot].rc = t[tot].cnt = 0;
return tot;
}
void insert(int &p, int l, int r, int delta, int val) {
if (!p) p = New();
t[p].cnt += val;
if (l == r) return;
int mid = (l + r) / 2;
if (delta <= mid)
insert(t[p].lc, l, mid, delta, val);
else
insert(t[p].rc, mid + 1, r, delta, val);
}
int merge(int p, int q) {
if (!p || !q)
return p ^ q;
t[p].cnt += t[q].cnt;
t[p].lc = merge(t[p].lc, t[q].lc);
t[p].rc = merge(t[p].rc, t[q].rc);
return p;
}
int ask(int p, int l, int r, int s, int e) {
if (s <= l && r <= e)
return t[p].cnt;
int mid = (l + r) / 2;
int val = 0;
if (s <= mid)
val += ask(t[p].lc, l, mid, s, e);
if (mid < e)
val += ask(t[p].rc, mid + 1, r, s, e);
return val;
}
// solve part
long long ans;
int size[N];
void search(int u, int fa) {
size[u] = 1;
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
if (v == fa) continue;
search(v, u);
size[u] += size[v];
}
}
long long sum[N];
void dfs(int u, int fa) {
int firv = 0, secv = 0;
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
if (v == fa) continue;
if (size[v] > firv) secv = firv, firv = size[v];
else if (size[v] > secv) secv = size[v];
}
if (n - size[u] > firv) secv = firv, firv = n - size[u];
else if (n - size[u] > secv) secv = n - size[u];
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
if (v == fa) continue;
add(size[v], 1), dfs(v, u), add(size[v], -1);
int m = size[v] == firv ? secv : firv;
int l = 2 * size[v] - n, r = n - 2 * m;
if (l > n || r < 1 || l > r) {
root[u] = merge(root[u], root[v]);
continue;
}
if (l < 1) l = 1;
if (r > n) r = n;
ans += 1ll * ask(root[v], 1, n, l, r) * u;
root[u] = merge(root[u], root[v]);
}
if (u == 1)
return;
int m = n - size[u] == firv ? secv : firv;
int l = 2 * (n - size[u]) - n, r = n - 2 * m;
if (l > n || r < 1 || l > r) {
insert(root[u], 1, n, size[u], 1);
return;
}
if (l < 1) l = 1;
if (r > n) r = n;
int cnt = 0;
cnt += sum[r] - sum[l - 1];
cnt -= ask(root[u], 1, n, l, r);
cnt -= calc(r) - calc(l - 1);
l = n - l, r = n - r, swap(l, r);
if (l < 1) l = 1;
if (r > n) r = n;
cnt += calc(r) - calc(l - 1);
ans += 1ll * cnt * u;
insert(root[u], 1, n, size[u], 1);
}
void work() {
memset(head, 0, sizeof(head));
memset(c, 0, sizeof(c));
memset(sum, 0, sizeof(sum));
memset(root, 0, sizeof(root));
ovo = 0, tot = 0, ans = 0;
n = read();
for (int i = 1; i < n; i ++) {
int u = read(), v = read();
addedge(u, v), addedge(v, u);
}
search(1, 0);
for (int i = 2; i <= n; i ++)
sum[size[i]] ++;
for (int i = 2; i <= n; i ++)
sum[i] += sum[i - 1];
dfs(1, 0);
printf("%lld\n", ans);
}
int main() {
int T = read();
while (T --) work();
return 0;
}

