重修贝尔曼方程，深刻体悟sar三件套之美

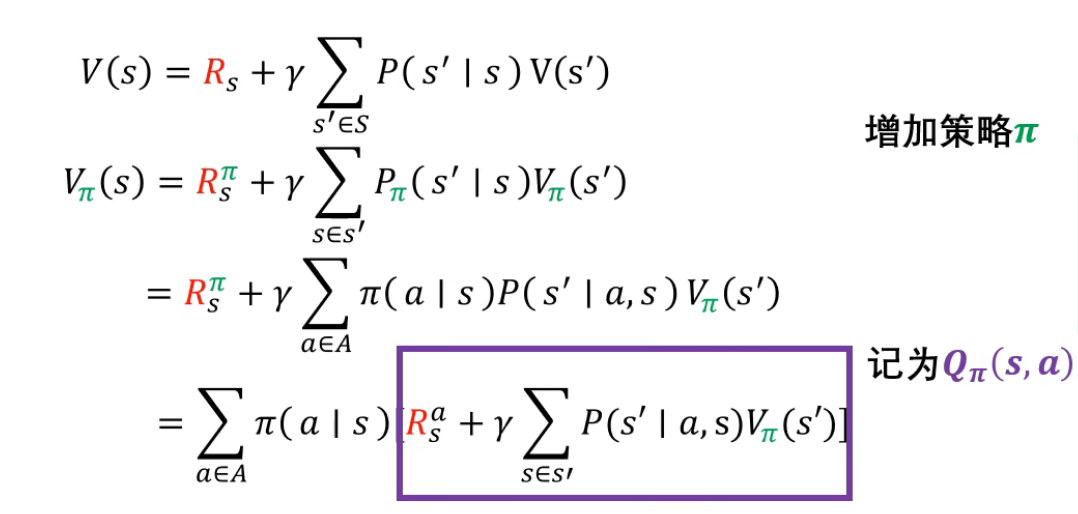
 我第一次学贝尔曼方程的时候，当时没有搞清楚VpaiS和Vs的区别，今天大概能理解了，那我讲一讲

 

先看Vs，就是他到达某个特定状态之后得到的奖励加上后面衰减常数乘上，一大串，一大串是什么呢，就是一个求和，求和的是什么呢，就是到达下一个状态的状态值（可以理解为预期奖励大小）乘上到达下一个状态的概率，类似于一个期望值，但是本质区别就是，Rs和R(pai)s,Rs是有了结果到达终点的奖励值，而R(pai)s,是你在原地思考，采取什么动作，你做所有动作的一个期望值

再看VpaiS,刚开始我只看到这个公式第一行，这是很抽象很难理解的，于是可以直接去看最后一行，有点恶心，求和嵌套求和，可以先不用那么复杂，可以先把最外面的求和符号拿掉方便理解，如果没有最后一行，我甚至不知道RpaiS是啥，它其实就是，状态S下，采用某个a(action)的概率乘上Rsa,就是在状态S下，采用a所得到的奖励，那么求和之后，就是你在状态S中，你做所有策略，就是你去行动，所有行动奖赏按比例分配的一个期望值，（就是你在某个状态，你动一下，的期望值，跟结果没关系）那么后面那一大串就是，你到达VpaiS'的一个pai型值乘上比例（到达的概率），也是一个求期望的方式

所以Vs可理解为，偏向结果

VpaiS更偏向过程action，就是可以看他后面叠加的衰减值的区别，V就是，你从s到s'状态的一个状态值期望，而V(pai)就是一个期望，就是你用尽心机，用尽所有方法达到目标的一个期望值

 

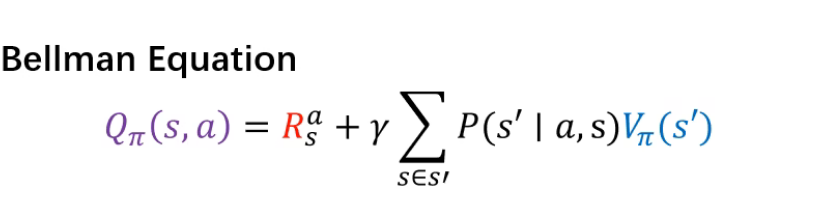
 所以这个Qpai（Sa）与上面V（pai）的区别就是，上面的V（pai）是对所有的a(action)求期望（海王），而Qpai（sa）是对某个特定的a进行分析，就是只就算了某个行为的奖励（纯情），没有对所有行为奖励求期望，他的衰减部分是加上"海王"的，就是采取这个特定方式，成为下一个状态的期望值，通过期望什么呢，因为S'未知，所以求，采取该方法，到达S'的期望对比这个对Vpai(s')按照比例求期望，这个比例也是基于，action是某个特定的a

 

 

理解一下上文Q(pai)计算时“海王V”前面的P，第一行就是，s到s'的概率，第二行它等于S状态下，采取a的概率乘上，采取a方法的条件下，达到终点s'的概率