P1758 [NOI2009]管道取珠
重点是我们要思考 \(\Sigma a_i^2\) 的意义是什么。
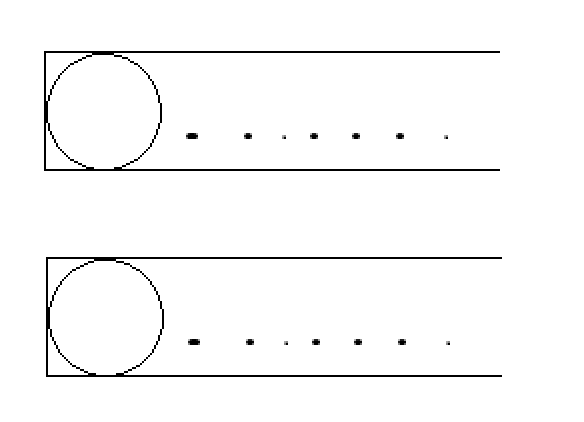
由题可得两个管道如图
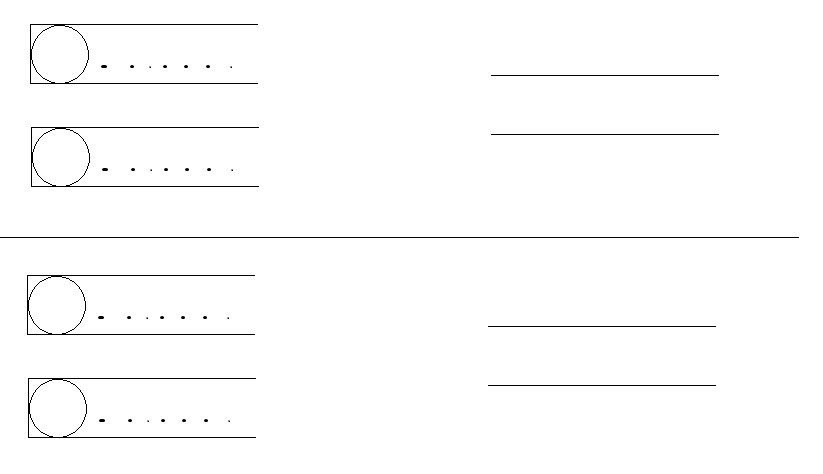
其中令可得出的每一种队列的种数为 \(a_i\) ,但是我们要求的是 \(a_i^2\),于是我们将这两个管道复制一遍,分为两组管道如下图,每次可从四个中的任意一个中取出一个放入其对应组的队列中,当这两个队列相同时由乘法原理可得种类数为 \(a_i^2\)。
然后我们看到数据范围 \(--\) \(n,m \leq 500\),相当于 \(O(n^3)\) 都可以过,于是我们可以想到动态规划。
我们令方程 \(f[k][i][j]\) 为构成的组数的平方的和,其中 \(k\) 为两组分别已经取出了 \(k\) 个数放入了对应的队列中, \(i\) 为第一组管道中的上管道已经取到了第 \(i\) 个,可以表示下管道已经取到了第 \(k-i\) 个, \(j\) 为第二组管道中的上管道已经取到了第 \(j\) 个,可以表示下管道已经取到了第 \(k-j\) 个。
我们可以转移时,当且仅当两组所取出的珠子颜色是相等的,如下图有四种情况:(我们定义上管道的珠子颜色存在 \(up\) 数组中,下管道的珠子颜色存在 \(dn\) 数组中)
- \(up[i]=up[j]\ f[k][i][j]+=f[k-1][i-1][j-1]\)
- \(up[i]=up[k-j]\ f[k][i][j]+=f[k-1][i-1][j]\)
- \(dn[k-i]=up[j]\ f[k][i][j]+=f[k-1][i][j-1]\)
- \(dn[k-i]=dn[k-j]\ f[k][i][j]+=f[k-1][i][j]\)
看不懂的童鞋请自行脑补一下取珠子的过程。
最后输出 \(f[n+m][n][n]\) 就可以了,但注意到 \(n+m\) 最大可以有 \(1000\), \(n\) 最大可以为500, $1000 * 50 * 500= 250000000\ $, \(128MB\) 的空间必然会炸掉,于是我们再滚动一下数组就可以了。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define in inline
#define ll long long
const int N=510,mod=1024523;
in int read()
{
int w=0,r=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')r=-1;
ch=getchar();
}
while(isdigit(ch))
{
w=(w<<1)+(w<<3)+(ch^48);
ch=getchar();
}
return w*r;
}
in ll get()
{
char ch;
cin>>ch;
return ch=='A'?1:0;
}
ll f[3][N][N];
ll up[N],dn[N];
in ll plu(ll x,ll y)
{
return x+y>=mod?x+y-mod:x+y;
}
in ll min_(ll x,ll y)
{
return x<y?x:y;
}
in ll max_(ll x,ll y)
{
return x>y?x:y;
}
int n,m;
int now;
int main()
{
// freopen("pearl.in","r",stdin);
// freopen("pearl.out","w",stdout);
n=read();
m=read();
for(int i=1;i<=n;i++)up[i]=get();
for(int i=1;i<=m;i++)dn[i]=get();
// for(int i=1;i<=n;i++)cout<<up[i]<<endl;
f[0][0][0]=1;
now=1;
for(int k=1;k<=(n+m);k++)
{
for(int i=0;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
f[now][i][j]=0;
}
}
for(int i=max_(0,k-m);i<=min_(n,k);i++)
{
for(int j=max_(0,k-m);j<=min_(n,k);j++)
{
if(i>0&&j>0&&up[i]==up[j])f[now][i][j]=plu(f[now][i][j],f[now^1][i-1][j-1]);
if(i>0&&k-j>0&&up[i]==dn[k-j])f[now][i][j]=plu(f[now][i][j],f[now^1][i-1][j]);
if(k-i>0&&k-j>0&&dn[k-i]==dn[k-j])f[now][i][j]=plu(f[now][i][j],f[now^1][i][j]);
if(k-i>0&&j>0&&dn[k-i]==up[j])f[now][i][j]=plu(f[now][i][j],f[now^1][i][j-1]);
}
}
now^=1;
}
cout<<f[now^1][n][n]<<endl;
return 0;
}
但是这份代码交在洛谷上只有\(90pts\),因为在滚动后,要清除上次所存储的结果,需要\((n+m)\times n \times n\)的复杂度,数据强一点一秒必然跑不完,于是我们只需要稍微改动一下转移方程,将由\(k\)之前的推出\(f[k][i][j]\)变为由\(f[k][i][j]\)推出\(k\)之后的,然后再将\(f[k][i][j]\)清零即可,代码如下:
#include<bits/stdc++.h>
using namespace std;
#define in inline
#define ll long long
const int N=510,mod=1024523;
in int read()
{
int w=0,r=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')r=-1;
ch=getchar();
}
while(isdigit(ch))
{
w=(w<<1)+(w<<3)+(ch^48);
ch=getchar();
}
return w*r;
}
in ll get()
{
char ch;
cin>>ch;
return ch=='A'?1:0;
}
ll f[3][N][N];
ll up[2*N],dn[2*N];
in ll plu(ll x,ll y)
{
return x+y>=mod?x+y-mod:x+y;
}
in ll min_(ll x,ll y)
{
return x<y?x:y;
}
in ll max_(ll x,ll y)
{
return x>y?x:y;
}
int n,m;
int now;
int main()
{
// freopen("pearl.in","r",stdin);
// freopen("pearl.out","w",stdout);
n=read();
m=read();
for(int i=1;i<=n;i++)up[i]=get();
for(int i=1;i<=m;i++)dn[i]=get();
// for(int i=1;i<=n;i++)cout<<up[i]<<endl;
f[0][0][0]=1;
now=0;
for(int k=0;k<(n+m);k++)
{
// for(int i=0;i<=n;i++)
// {
// for(int j=0;j<=n;j++)
// {
// f[now][i][j]=0;
// }
// }
for(int i=0;i<=min_(n,k);i++)
{
for(int j=0;j<=min_(n,k);j++)
{
if(!f[now][i][j]) continue;
if(up[i+1]==up[j+1])f[now^1][i+1][j+1]=plu(f[now^1][i+1][j+1],f[now][i][j]);
if(up[i+1]==dn[k-j+1])f[now^1][i+1][j]=plu(f[now^1][i+1][j],f[now][i][j]);
if(dn[k-i+1]==dn[k-j+1])f[now^1][i][j]=plu(f[now^1][i][j],f[now][i][j]);
if(dn[k-i+1]==up[j+1])f[now^1][i][j+1]=plu(f[now^1][i][j+1],f[now][i][j]);
f[now][i][j]=0;
}
}
now^=1;
}
cout<<f[now][n][n]<<endl;
return 0;
}
其实 \(reverse\) 与否都无所谓,正序逆序不影响。事实上这道题要想到开两组管道是比较难的,所以思维难度还是比较大,考试的时候基本上忽略了平方的意义。