圆方树简介(UOJ30:CF Round #278 Tourists)
我写这篇博客的原因
证明我也是学过圆方树的
顺便存存代码
前置技能
双联通分量:点双
然后就没辣
圆方树
建立
新建一个图
定义原图中的所有点为圆点
对于每个点双联通分量(只有两个点的也算)
建立一个方点,向所有的点双内的点连边
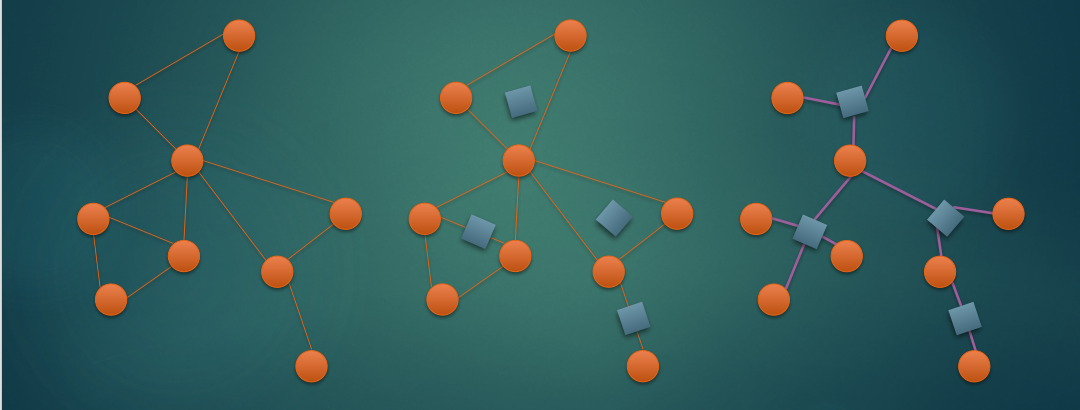
性质
- 一定是个森林
- 每个点双有唯一的方点
- 圆点方点相间分布,相同点不相邻
等等
例子 1
题面
求可以出现在两点之间的简单路路径上的点的最大权值,不带修改
分析
考虑用圆方树来解决
设圆点权值为本身,方点权值为点双中的最大权值
那么就是树上的路径最大权值
例子 2
还是上面的题,可以修改一个点的权值
类似题UOJ
用老方法
每次修改时更改圆点连接的所有方点
没了?
不存在的,这样每次修改是\(O(n)\)的,容易被卡
换一种定义:方点权值不包括它的父亲圆点
那么每次修改就只要修改圆点的父亲
注意如果\(lca\)是方点,还要算上它父亲方点的权值
堆+线段树(zkw辣)+树剖+圆方树+tarjan
UOJ代码
# include <bits/stdc++.h>
# define RG register
# define IL inline
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(4e5 + 5);
IL int Input(){
RG int x = 0, z = 1; RG char c = getchar();
for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + (c ^ 48);
return x * z;
}
struct Edge{
int next[_], first[_], to[_], cnt;
IL void Init(){
Fill(first, -1);
}
IL void Add(RG int u, RG int v){
next[cnt] = first[u], to[cnt] = v, first[u] = cnt++;
}
} G1, G2;
struct Segment{
int mn[_ << 2], M;
IL void Init(RG int n){
Fill(mn, 127);
for(M = 1; M < n; M <<= 1);
}
IL void Update(RG int x, RG int y){
x += M - 1, mn[x] = y;
for(x >>= 1; x; x >>= 1) mn[x] = min(mn[x << 1], mn[x << 1 | 1]);
}
IL int Query(RG int l, RG int r){
RG int ret = 2e9;
for(l += M - 2, r += M; l ^ r ^ 1; l >>= 1, r >>= 1){
if(~l & 1) ret = min(ret, mn[l ^ 1]);
if(r & 1) ret = min(ret, mn[r ^ 1]);
}
return ret;
}
} T;
struct Heap{
priority_queue <int> Q1, Q2;
IL void Push(RG int x){
Q1.push(-x);
}
IL void Del(RG int x){
Q2.push(-x);
}
IL int Top(){
while(!Q2.empty() && Q1.top() == Q2.top()) Q1.pop(), Q2.pop();
return -Q1.top();
}
} Q[_];
int tmp, n, m, q, val[_], dfn[_], low[_], Index, S[_];
int size[_], top[_], fa[_], deep[_], son[_];
IL void Tarjan(RG int u){
dfn[u] = low[u] = ++Index, S[++S[0]] = u;
for(RG int e = G1.first[u]; e != -1; e = G1.next[e]){
RG int v = G1.to[e], x;
if(!dfn[v]){
Tarjan(v), low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]){
val[++n] = 2e9, x = 0;
do{
x = S[S[0]--];
G2.Add(n, x), G2.Add(x, n);
} while(x != v);
G2.Add(n, u), G2.Add(u, n);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
IL void Dfs1(RG int u){
size[u] = 1;
if(u <= tmp && fa[u]) Q[fa[u]].Push(val[u]);
for(RG int e = G2.first[u]; e != -1; e = G2.next[e]){
RG int v = G2.to[e];
if(size[v]) continue;
fa[v] = u, deep[v] = deep[u] + 1;
Dfs1(v);
size[u] += size[v];
if(size[v] > size[son[u]]) son[u] = v;
}
}
IL void Dfs2(RG int u, RG int Top){
dfn[u] = ++Index, top[u] = Top;
if(son[u]) Dfs2(son[u], Top);
for(RG int e = G2.first[u]; e != -1; e = G2.next[e])
if(!dfn[G2.to[e]]) Dfs2(G2.to[e], G2.to[e]);
}
IL int Query(RG int u, RG int v){
RG int ret = 2e9;
while(top[u] ^ top[v]){
if(deep[top[u]] > deep[top[v]]) swap(u, v);
ret = min(ret, T.Query(dfn[top[v]], dfn[v]));
v = fa[top[v]];
}
if(dfn[u] > dfn[v]) swap(u, v);
ret = min(ret, T.Query(dfn[u], dfn[v]));
if(u > tmp) ret = min(ret, val[fa[u]]);
return ret;
}
int main(RG int argc, RG char* argv[]){
G1.Init(), G2.Init();
tmp = n = Input(), m = Input(), q = Input();
for(RG int i = 1; i <= n; ++i) val[i] = Input();
for(RG int i = 1; i <= m; ++i){
RG int u = Input(), v = Input();
G1.Add(u, v), G1.Add(v, u);
}
for(RG int i = 1; i <= tmp; ++i) if(!dfn[i]) Tarjan(i);
Fill(dfn, 0), Index = 0, T.Init(n);
Dfs1(1), Dfs2(1, 1);
for(RG int i = 1; i <= n; ++i) T.Update(dfn[i], val[i]);
for(RG int i = tmp + 1; i <= n; ++i) T.Update(dfn[i], Q[i].Top());
for(RG int i = 1, a, b; i <= q; ++i){
RG char op; scanf(" %c", &op);
a = Input(), b = Input();
if(op == 'C'){
if(fa[a]) Q[fa[a]].Del(val[a]);
val[a] = b, T.Update(dfn[a], val[a]);
if(fa[a]) Q[fa[a]].Push(val[a]);
if(fa[a]) T.Update(dfn[fa[a]], Q[fa[a]].Top());
}
else printf("%d\n", Query(a, b));
}
return 0;
}


