洛谷 P1282 多米诺骨牌

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

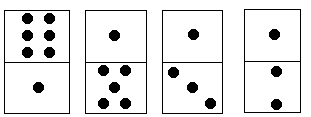
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式：

 

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

 

输出格式：

 

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

 

输入输出样例

输入样例#1：

4
6 1
1 5
1 3
1 2

输出样例#1：

1

 

 

 就是个背包的变形。。。

   我们定义f[i][j]代表前I个多米诺骨牌的差值为j时的最小旋转次数，那么状态转移方程就很显然了：

   记a，b分别为一个骨牌的上下的点数，则

   f[i][j]=min(f[i][j],min(f[i-1][j-(a-b)+5000],f[i-1][j-(b-a)+5000]+1))

                                     不旋转                             旋转

   其中要加上5000就是要加上一个偏移量，防止下标为负数

   初始化时将数组初始化为999999999，f[0][5000]=0

   查询时就从5000开始向两端扩展，若它们两个取的f数组值不为999999999，就说明可以达到这个最小值，输出这个次数即可。

 

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#define RG register
#define IL inline
#define pi acos(-1.0)
#define ll long long 
using namespace std;
int a[1005][3],n;
int w1[1005],w2[1005];
int dp[1005][10005];
int main() {
  scanf("%d",&n);
  for(int i=1;i<=n;i++){
     int k1,k2;
     scanf("%d%d",&k1,&k2);
     w1[i]=k1-k2; w2[i]=k2-k1; //w1不翻转，w2翻转
  }
  for(int i=0;i<=n;i++)
     for(int j=0;j<=10002;j++)
        dp[i][j]=999999999;//前I个多米诺牌，差值和为j的最小次数
  dp[0][5000]=0;
  for(int i=1;i<=n;i++)
     for(int j=-5000;j<=5000;j++)
       dp[i][j+5000]=min(dp[i][j+5000],min(dp[i-1][j-w1[i]+5000],dp[i-1][j-w2[i]+5000]+1));
  if(dp[n][5000]!=999999999){
     cout<<dp[n][5000];
     return 0;
  }
  int j=1,minn=999999999;
  while(1){
    minn=min(dp[n][5000-j],dp[n][5000+j]);
    if(minn!=999999999){
       cout<<minn;
       return 0;
    }
    ++j;
  }
  return 0;
}