《神经网络与机器学习》学习笔记——第1章 感知器
这是本人学习《神经网络与机器学习》时查找各种资料的总结的笔记,为了让自己的印象更深刻并且分享些经验出来,最后有C#与MATLAB的代码实现。
如果有不对的地方欢迎指点。
这里需要有一定的数学基础,如:线性代数,微积分,矩阵,概率,统计等。
目录:
一、概念
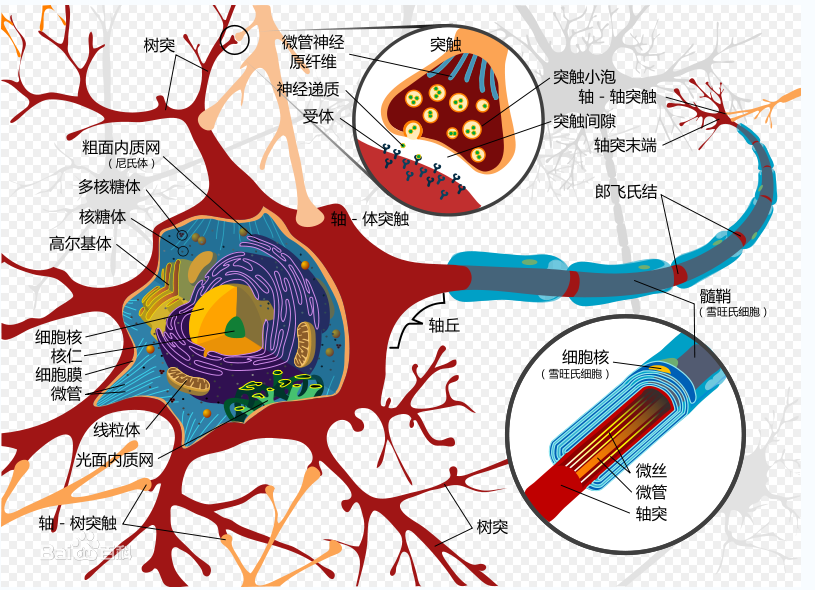
感知器是生物神经细胞的简单抽象,神经细胞结构大致可分为:树突、突触、细胞体及轴突。
单个神经细胞可被视为一种只有两种状态的机器——激动时为‘是’,而未激动时为‘否’。神经细胞的状态取决于从其它的神经细胞收到的输入信号量,及突触的强度(抑制或加强)。当信号量总和超过了某个阈值时,细胞体就会激动,产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。为了模拟神经细胞行为,与之对应的感知机基础概念被提出,如权值(突触)、偏置(阈值)及激活函数(细胞体)。
1.感知器是使用特征向量来表示的前馈式人工神经网络,它是一种二元分类器,把矩阵上的输入(实数值向量)映射到输出值。由于输入直接经过权重关系转换为输出,所以感知机可以被视为最简单形式的前馈式人工神经网络。它是建立在一个非线性神经元上,即神经元的 McCulloch-Pitts 模型。
2.神经元模型是一个线性组合器和随后的硬限幅器(激活函数)组合(如下图1.1)。

图1.1
感知器的输入值记为: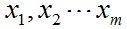 ,权值记为:
,权值记为: ,偏置值记为:b。
,偏置值记为:b。
输入值:表示将要分类的事物的特性的组合,对应每个神经细胞接收到外部输入的刺激信号,即:初始特征。
权值:表示该模型的分类变化参数,也是该模型在学习过程中需要计算出的参数。
偏置值(Bias Units):它是一个不依赖于任何输入值的常数。可以认为是激活函数的偏移量,或者给神经元一个基础活跃等级。从空间上看(如:图1.2),该值的作用仅仅是把决策边界(图1.2)从原点移开。
诱导局部域:每一个输入值与其对应的权值相乘,然后将这些乘积的结果相加得到的结果,即:v 的值(PS:这概念是本人在看《神经网络与机器学习》一书的译本中看到的)。
公式1.1

硬限幅器(激活函数):使用诱导局部域作为输入参数,当输入为正时,感知器输出 +1,反之则输出 -1。
公式1.2
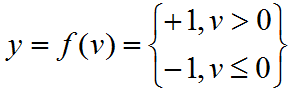
3.感知器的目的是把输入值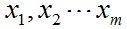 所表示的点正确的分为
所表示的点正确的分为 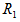 或者
或者 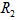 两类。
两类。
感知器的分类的规则是:
①感知器的输出值 y 是 +1 就将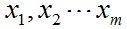 表示的点分配给
表示的点分配给 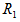 类。
类。
②感知器的输出值 y 是 -1 就将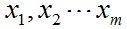 表示的点分配给
表示的点分配给 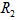 类。
类。
4.决策边界。
根据前面两点,可得出:
①当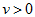 时,
时,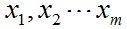 属于
属于 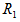 类。
类。
②当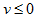 时,
时,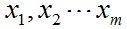 属于
属于 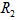 类。
类。
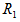
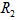 两个区域,则决策边界超平面定义是:
两个区域,则决策边界超平面定义是: 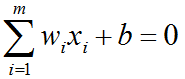
该图中决策边界是条直线,位于边界线上面的两个绿点分入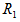 ,位于边界线下面的两个红点分入
,位于边界线下面的两个红点分入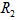 。
。
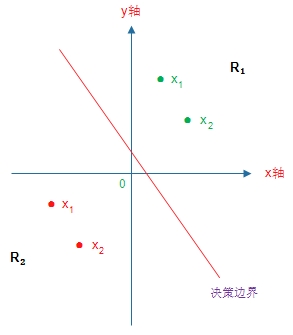
图1.2
5.感知器只能对线性可分的两个类进行分类。
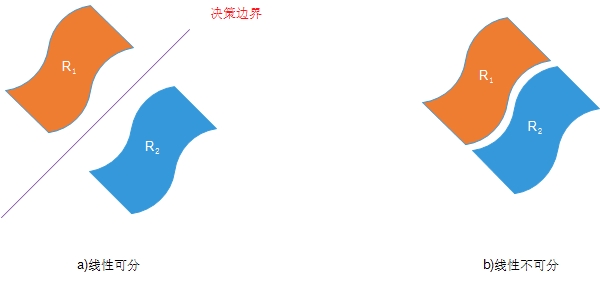
图1.3
二、感知器学习
首先,这里引用了一张在帖吧上看到的一张图片:

图1.4
我们看到上图的汽车的时候,会记忆它的一些基本特征(比如:有4个轮子,车身灰白色等等),如果没有人告诉我们“车”的概念,我们虽然记下了它的大概基本特征,但却并不知道它是什么。同样,如果有人告诉我们“车”是什么,但我们却从来没有看见过车,同样对“车”一无所知。只有我们看到过车并记忆了它的一些基本特征,并且有人告诉我们,这就是“车”,当我们再次看到相似的事物的时候,我们自然就会判断,这就是“车”。
感知器也一样,给出待分类的几个点( ),就如同我们人只见过“车”但却没有“车”这一概念时一样并不知道这就是“车”这一种类,感知器是无法知道它们是属于
),就如同我们人只见过“车”但却没有“车”这一概念时一样并不知道这就是“车”这一种类,感知器是无法知道它们是属于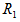 类还是
类还是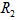 类。
类。
这时,我们需要让感知器正确的识别出是属于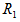 类还是
类还是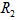 类的过程,就是感知器学习(训练)的过程,而在学习(训练)过程中需要使用的已分类好的一组数据,就是训练样本,当感知器完成了学习(训练)之后,就能正确的识别与分类了。
类的过程,就是感知器学习(训练)的过程,而在学习(训练)过程中需要使用的已分类好的一组数据,就是训练样本,当感知器完成了学习(训练)之后,就能正确的识别与分类了。
------------------------------------------------------------------------------------------------
示例1:

------------------------------------------------------------------------------------------------
三、误差修正学习算法
误差修正学习算法是通过多次迭代的方式来调整感知器的权值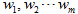 ,使感知器的输出信号 y 的值逐渐逼近给定训练样本的输出值。
,使感知器的输出信号 y 的值逐渐逼近给定训练样本的输出值。
在上面的示例1中,使用误差修正学习算法即可找到一组合适的权值(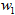 和
和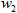 )以完成训练。
)以完成训练。
设:
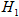 是训练样本
是训练样本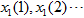 中,属于
中,属于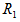 类的样本所组成的子集,
类的样本所组成的子集,
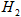 是训练样本
是训练样本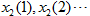 中,属于
中,属于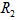 类的样本所组成的子集,
类的样本所组成的子集,
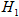 和
和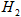 的并集是整个训练样本集
的并集是整个训练样本集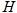 ,n 是训练样本个数(迭代次数),给定训练样本集
,n 是训练样本个数(迭代次数),给定训练样本集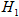 和
和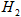 来训练感知器,训练过程中对权值向量
来训练感知器,训练过程中对权值向量  的调整使两个类
的调整使两个类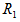 和
和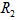 线性可分,
线性可分,
即:
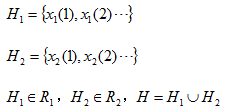
也就是说,存在一个权值  具有以下性质:
具有以下性质:
公式1.4

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
补充说明:
在示例1中,训练样本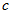 是坐标轴上的一个点,因此该点的初始特征就是坐标
是坐标轴上的一个点,因此该点的初始特征就是坐标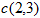 ,因此,输入值就有两个,所以对应的权值
,因此,输入值就有两个,所以对应的权值 也有两个,所以使用矩阵的形式来表示公式1.1,则是:
也有两个,所以使用矩阵的形式来表示公式1.1,则是: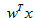 。
。
所以,感知器的训练问题就是找到一组权值向量  满足公式1.4中的两个不等式。
满足公式1.4中的两个不等式。
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
使感知器的权值自适应的算法现在可以用以下公式来描述:
1.假设训练集合的第 n 个成员 x(n)
根据算法中的第
n 次迭代的权值向量 w(n)
能正确分类,那么感知器的权值向量按下述规则不做修改:
公式1.5

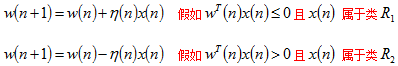
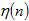


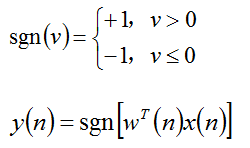

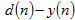
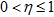

/// <summary> /// 矩阵。 /// </summary> public class Matrix { #region 字段 /// <summary> /// 矩阵数据。 /// </summary> private readonly double[][] _data; #endregion 字段 #region 初始化 /// <summary> /// 初始化。 /// </summary> /// <param name="row">行=列。</param> public Matrix(int row) : this(row, row) { } /// <summary> /// 初始化。 /// </summary> /// <param name="row">行。</param> /// <param name="column">列。</param> public Matrix(int row, int column) { Row = row; Column = column; _data = new double[row][]; for (var index = 0; index < row; index++) { _data[index] = new double[column]; } } /// <summary> /// 初始化。 /// </summary> /// <param name="row">行。</param> /// <param name="column">列。</param> /// <param name="value">初始值。</param> public Matrix(int row, int column, double value) : this(row, column, index => value) { } /// <summary> /// 初始化。 /// </summary> /// <param name="row">行。</param> /// <param name="column">列。</param> /// <param name="func">初始值计算方法。</param> public Matrix(int row, int column, Func<int, double> func) { Row = row; Column = column; _data = new double[row][]; for (var index = 0; index < row; index++) { _data[index] = new double[column]; if (func != null) { for (var loop = 0; loop < column; loop++) { _data[index][loop] = func(loop); } } } } /// <summary> /// 初始化。 /// </summary> /// <param name="matrix">矩阵。</param> public Matrix(double[][] matrix) { if (matrix == null || matrix.Length <= 0) throw new ArgumentNullException(nameof(matrix)); Row = matrix.Length; Column = matrix[0].Length; _data = matrix; } /// <summary> /// 复制矩阵。 /// </summary> /// <param name="matrix">矩阵。</param> public Matrix(Matrix matrix) { var row = matrix.Row; var column = matrix.Column; Row = row; Column = column; _data = new double[row][]; for (var rowNumber = 0; rowNumber < row; rowNumber++) { _data[rowNumber] = new double[column]; for (var columnNumber = 0; columnNumber < column; columnNumber++) { this[rowNumber, columnNumber] = matrix[rowNumber, columnNumber]; } } } /// <summary> /// 生成均匀分布在(0-1)之间伪随机数的矩阵。 /// </summary> /// <param name="row">行。</param> /// <param name="column">列。</param> /// <returns>矩阵。</returns> public static Matrix CreateRandMatrix(int row, int column) { return new Matrix(row, column, index => RandomToolit.GetRandom().NextDouble()); } #endregion 初始化 #region 属性 /// <summary> /// 返中行数。 /// </summary> public int Row { get; } /// <summary> /// 返回列数。 /// </summary> public int Column { get; } public double this[int row, int column] { get { return _data[row][column]; } set { _data[row][column] = value; } } #endregion 属性 #region 操作符 /// <summary> /// 矩阵加法 binary addition。 /// </summary> /// <param name="lhs"></param> /// <param name="rhs"></param> /// <returns></returns> public static Matrix operator +(Matrix lhs, Matrix rhs) { if (lhs.Row != rhs.Row) { throw new Exception("相加的两个矩阵的行数不等"); } if (lhs.Column != rhs.Column) { throw new Exception("相加的两个矩阵的列数不等"); } var row = lhs.Row; var column = lhs.Column; var ret = new Matrix(row, column); for (var index = 0; index < row; index++) { for (var loop = 0; loop < column; loop++) { var value = lhs[index, loop] + rhs[index, loop]; ret[index, loop] = value; } } return ret; } /// <summary> /// 矩阵减法 binary subtraction。 /// </summary> /// <param name="lhs"></param> /// <param name="rhs"></param> /// <returns></returns> public static Matrix operator -(Matrix lhs, Matrix rhs) { if (lhs.Row != rhs.Row) { throw new Exception("相减的两个矩阵的行数不等"); } if (lhs.Column != rhs.Column) { throw new Exception("相减的两个矩阵的列数不等"); } var row = lhs.Row; var column = lhs.Column; var ret = new Matrix(row, column); for (var index = 0; index < row; index++) { for (var loop = 0; loop < column; loop++) { var value = lhs[index, loop] - rhs[index, loop]; ret[index, loop] = value; } } return ret; } /// <summary> /// 矩阵乘法(乘积)。 /// </summary> /// <remarks> /// 当矩阵A的列数等于矩阵B的行数时,A与B可以相乘。 /// 1.矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。 /// 2.乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。 /// </remarks> /// <param name="lhs"></param> /// <param name="rhs"></param> /// <returns></returns> public static Matrix operator *(Matrix lhs, Matrix rhs) { if (lhs.Column != rhs.Row) { throw new Exception("相乘的两个矩阵的行列数不匹配"); } var ret = new Matrix(lhs.Row, rhs.Column); for (var index = 0; index < lhs.Row; index++) { for (var loop = 0; loop < rhs.Column; loop++) { double temp = 0; for (var k = 0; k < lhs.Column; k++) { temp += lhs[index, k] * rhs[k, loop]; } ret[index, loop] = temp; } } return ret; } /// <summary> /// 矩阵除法 binary division。 /// </summary> /// <param name="lhs"></param> /// <param name="rhs"></param> /// <returns></returns> public static Matrix operator /(Matrix lhs, Matrix rhs) { return lhs * rhs.Inverse(); } /// <summary> /// 单目加 unary addition。 /// </summary> /// <param name="sourceMatrix"></param> /// <returns></returns> public static Matrix operator +(Matrix sourceMatrix) { var returnMatrix = new Matrix(sourceMatrix); for (var rowNumber = 0; rowNumber < returnMatrix.Row; rowNumber++) { for (var columnNumber = 0; columnNumber < returnMatrix.Column; columnNumber++) { returnMatrix[rowNumber, columnNumber] = +returnMatrix[rowNumber, columnNumber]; } } return returnMatrix; } /// <summary> /// 单目减 unary subtraction。 /// </summary> /// <param name="sourceMatrix"></param> /// <returns></returns> public static Matrix operator -(Matrix sourceMatrix) { var returnMatrix = new Matrix(sourceMatrix); for (var rowNumber = 0; rowNumber < returnMatrix.Row; rowNumber++) { for (var columnNumber = 0; columnNumber < returnMatrix.Column; columnNumber++) { returnMatrix[rowNumber, columnNumber] = -returnMatrix[rowNumber, columnNumber]; } } return returnMatrix; } /// <summary> /// 矩阵加法。 /// </summary> /// <param name="m"></param> /// <param name="d"></param> /// <returns></returns> public static Matrix operator +(Matrix m, double d) { var ret = new Matrix(m); for (var rowNumber = 0; rowNumber < ret.Row; rowNumber++) for (var columnNumber = 0; columnNumber < ret.Column; columnNumber++) ret[rowNumber, columnNumber] += d; return ret; } /// <summary> /// 矩阵加法。 /// </summary> /// <param name="d"></param> /// <param name="m"></param> /// <returns></returns> public static Matrix operator +(double d, Matrix m) { var ret = new Matrix(m); for (var i = 0; i < ret.Row; i++) for (var j = 0; j < ret.Column; j++) ret[i, j] += d; return ret; } /// <summary> /// 矩阵减法。 /// </summary> /// <param name="sourceMatrix"></param> /// <param name="d"></param> /// <returns></returns> public static Matrix operator -(Matrix sourceMatrix, double d) { var targetMatrix = new Matrix(sourceMatrix); for (var rowNumber = 0; rowNumber < targetMatrix.Row; rowNumber++) for (var columnNumber = 0; columnNumber < targetMatrix.Column; columnNumber++) targetMatrix[rowNumber, columnNumber] -= d; return targetMatrix; } /// <summary> /// 矩阵减法。 /// </summary> /// <param name="d"></param> /// <param name="sourceMatrix"></param> /// <returns></returns> public static Matrix operator -(double d, Matrix sourceMatrix) { var targetMatrix = new Matrix(sourceMatrix); for (var rowNumber = 0; rowNumber < targetMatrix.Row; rowNumber++) for (var columnNumber = 0; columnNumber < targetMatrix.Column; columnNumber++) targetMatrix[rowNumber, columnNumber] = d - targetMatrix[rowNumber, columnNumber]; return targetMatrix; } /// <summary> /// 数乘 number multiple。 /// </summary> /// <param name="m"></param> /// <param name="d"></param> /// <returns></returns> public static Matrix operator *(Matrix m, double d) { var ret = new Matrix(m); for (var rowNumber = 0; rowNumber < ret.Row; rowNumber++) for (var columnNumber = 0; columnNumber < ret.Column; columnNumber++) ret[rowNumber, columnNumber] *= d; return ret; } /// <summary> /// 数乘 number multiple。 /// </summary> /// <param name="d"></param> /// <param name="m"></param> /// <returns></returns> public static Matrix operator *(double d, Matrix m) { var ret = new Matrix(m); for (var i = 0; i < ret.Row; i++) for (var j = 0; j < ret.Column; j++) ret[i, j] *= d; return ret; } /// <summary> /// 数除 number division。 /// </summary> /// <param name="sourceMatrix"></param> /// <param name="d"></param> /// <returns></returns> public static Matrix operator /(Matrix sourceMatrix, double d) { var targetMatrix = new Matrix(sourceMatrix); for (var rowNumber = 0; rowNumber < targetMatrix.Row; rowNumber++) for (var columnNumber = 0; columnNumber < targetMatrix.Column; columnNumber++) targetMatrix[rowNumber, columnNumber] /= d; return targetMatrix; } /// <summary> /// 数除 number division。 /// </summary> /// <param name="d"></param> /// <param name="sourceMatrix"></param> /// <returns></returns> public static Matrix operator /(double d, Matrix sourceMatrix) { var targetMatrix = new Matrix(sourceMatrix); for (var rowNumber = 0; rowNumber < targetMatrix.Row; rowNumber++) for (var columnNumber = 0; columnNumber < targetMatrix.Column; columnNumber++) targetMatrix[rowNumber, columnNumber] = d / targetMatrix[rowNumber, columnNumber]; return targetMatrix; } #endregion 操作符 #region 矩阵乘法(点积) /// <summary> /// 矩阵乘法(点积)。 /// </summary> /// <param name="target"></param> /// <returns></returns> public Matrix DotMultiple(Matrix target) { if (target == null) throw new ArgumentNullException(nameof(target)); if (target.Row != Row || target.Column != Column) throw new ArgumentException("矩阵维度不一致"); var ret = new Matrix(target); for (var rowNumber = 0; rowNumber < ret.Row; rowNumber++) for (var columnNumber = 0; columnNumber < ret.Column; columnNumber++) ret[rowNumber, columnNumber] = this[rowNumber, columnNumber] * target[rowNumber, columnNumber]; return ret; } #endregion 矩阵乘法(点积) #region 初等变换 /// <summary> /// 初等变换 primary change。 /// </summary> /// <remarks> /// 对调两行:ri←→rj。 /// </remarks> /// <param name="row"></param> /// <param name="column"></param> /// <returns></returns> public Matrix Exchange(int row, int column) { for (var index = 0; index < Column; index++) { var temp = this[row, index]; this[row, index] = this[column, index]; this[column, index] = temp; } return this; } /// <summary> /// 初等变换,第 index 行乘以 mul。 /// </summary> /// <param name="index">行号。</param> /// <param name="mul"></param> /// <returns></returns> private Matrix Multiple(int index, double mul) { for (var loop = 0; loop < Column; loop++) { this[index, loop] *= mul; } return this; } /// <summary> /// 初等变换,第 src 行乘以 mul 加到第 index 行。 /// </summary> /// <param name="index"></param> /// <param name="src"></param> /// <param name="mul"></param> /// <returns></returns> private Matrix MultipleAdd(int index, int src, double mul) { for (var loop = 0; loop < Column; loop++) { this[index, loop] += this[src, loop] * mul; } return this; } #endregion 初等变换 #region unit matrix:设为单位阵 /// <summary> /// unit matrix:设为单位阵。 /// </summary> public void SetUnit() { for (int i = 0; i < _data.GetLength(0); i++) for (int j = 0; j < _data.GetLength(1); j++) this[i, j] = ((i == j) ? 1 : 0); } #endregion unit matrix:设为单位阵 #region 逆阵 inversion:使用矩阵的初等变换,列主元素消去法 /// <summary> /// 逆阵 inversion:使用矩阵的初等变换,列主元素消去法。 /// </summary> /// <returns></returns> public Matrix Inverse() { if (Row != Column) { throw new Exception("求逆的矩阵不是方阵"); } var tmp = new Matrix(this); //单位阵 var ret = new Matrix(Row); ret.SetUnit(); double dMul; for (int i = 0; i < Row; i++) { var maxIndex = tmp.Pivot(i); if (tmp[maxIndex, i] == 0) { throw new Exception("求逆的矩阵的行列式的值等于0,"); } //下三角阵中此列的最大值不在当前行,交换 if (maxIndex != i) { tmp.Exchange(i, maxIndex); ret.Exchange(i, maxIndex); } ret.Multiple(i, 1 / tmp[i, i]); tmp.Multiple(i, 1 / tmp[i, i]); for (int j = i + 1; j < Row; j++) { dMul = -tmp[j, i] / tmp[i, i]; tmp.MultipleAdd(j, i, dMul); } } for (int i = Row - 1; i > 0; i--) { for (int j = i - 1; j >= 0; j--) { dMul = -tmp[j, i] / tmp[i, i]; tmp.MultipleAdd(j, i, dMul); ret.MultipleAdd(j, i, dMul); } } return ret; } #endregion 逆阵 inversion:使用矩阵的初等变换,列主元素消去法 #region 转置 transpose /// <summary> /// 转置 transpose。 /// </summary> /// <returns>矩阵。</returns> public Matrix Transpose() { var ret = new Matrix(Column, Row); for (var index = 0; index < Row; index++) { for (var loop = 0; loop < Column; loop++) { ret[loop, index] = this[index, loop]; } } return ret; } #endregion 转置 transpose #region 复制和平铺矩阵 /// <summary> /// 复制和平铺矩阵。 /// </summary> /// <remarks> /// repmat = Replicate Matrix。 /// 示例: /// B = A.Replicate(m,n),就是创建一个矩阵 B,B 中复制了共 m * n 个 A 矩阵,因此 B 矩阵的大小为 [A.Row * m, A.Col * m]。 /// 即:A 是一个 5 行 3 列的矩阵,则 B 为 5 * m 行 3 * n 列的矩阵。 /// </remarks> /// <param name="row">行数。</param> /// <param name="column">列数。</param> /// <returns>矩阵。</returns> public Matrix Repmat(int row = 1, int column = 1) { if (row <= 0) throw new ArgumentException("矩阵行数必须大于 0"); if (column <= 0) throw new ArgumentException("矩阵行数必须大于 0"); var matrix = new Matrix(Row * row, Column * column); for (var index = 0; index < matrix.Row; index++) { for (var loop = 0; loop < matrix.Column; loop++) { matrix[index, loop] = this[index % Row, loop % Column]; } } return matrix; } #endregion 复制和平铺矩阵 #region 调整矩阵的行数、列数和维数 /// <summary> /// 调整矩阵的行数、列数和维数。 /// </summary> /// <param name="row">新矩阵的行数。</param> /// <param name="column">新矩阵的列数。</param> /// <returns>矩阵。</returns> public Matrix Reshape(int row, int column) { return Reshape(this, row, column); } /// <summary> /// 调整矩阵的行数、列数和维数。 /// </summary> /// <param name="source">源矩阵。</param> /// <param name="row">新矩阵的行数。</param> /// <param name="column">新矩阵的列数。</param> /// <returns>矩阵。</returns> public static Matrix Reshape(Matrix source, int row, int column) { if (source == null) throw new ArgumentNullException(nameof(source)); if (source.Row * source.Column != row * column) throw new ArgumentException("元素的个数(row * column)必须是源矩阵一致"); var data = new Matrix(row, column); var newColumnNumber = 0; var newRowNumber = 0; for (var sourceColumnNumber = 0; sourceColumnNumber < source.Column; sourceColumnNumber++) { for (var sourceRowNumber = 0; sourceRowNumber < source.Row; sourceRowNumber++) { data[newRowNumber, newColumnNumber] = source[sourceRowNumber, sourceColumnNumber]; newRowNumber++; if (newRowNumber >= row) { newRowNumber = 0; newColumnNumber++; } } } return data; } #endregion 调整矩阵的行数、列数和维数 #region 返回列主元素的行号 /// <summary> /// 返回列主元素的行号。 /// </summary> /// <remarks> /// 在行号 [row, Col) 范围内查找第 row 列中绝对值最大的元素,返回所在行号。 /// </remarks> /// <param name="row">开始查找的行号。</param> /// <returns>行号。</returns> private int Pivot(int row) { int index = row; for (int i = row + 1; i < Row; i++) { if (this[i, row] > this[index, row]) index = i; } return index; } #endregion 返回列主元素的行号 #region 获得指定行的数据 /// <summary> /// 获得指定行的数据。 /// </summary> /// <param name="rowNumber">行号。</param> /// <returns>行数据。</returns> public double[] GetRow(int rowNumber) { if (rowNumber < 0 || rowNumber >= Row) throw new ArgumentException("行号不正确", nameof(rowNumber)); return _data[rowNumber]; } #endregion 获得指定行的数据 #region 获得指定列的数据 /// <summary> /// 获得指定列的数据。 /// </summary> /// <param name="columnNumber">列号。</param> /// <returns>列数据。</returns> public double[] GetColumn(int columnNumber) { if (columnNumber < 0 || columnNumber >= Column) throw new ArgumentException("列号不正确", nameof(columnNumber)); var column = new double[Row]; for (var rowNumber = 0; rowNumber < Row; rowNumber++) { column[rowNumber] = _data[rowNumber][columnNumber]; } return column; } #endregion 获得指定列的数据 #region 转换字符串 /// <summary> /// 转换字符串。 /// </summary> /// <returns>矩阵字符串。</returns> public override string ToString() { var maxLength = 0; for (var rowNumber = 0; rowNumber < Row; rowNumber++) { for (var columnNumber = 0; columnNumber < Column; columnNumber++) { var length = this[rowNumber, columnNumber].ToString(CultureInfo.InvariantCulture).Length; if (length > maxLength) { maxLength = length; } } } maxLength += 3; var printBuilder = new StringBuilder(); for (var rowNumber = 0; rowNumber < Row; rowNumber++) { if (rowNumber > 0) { printBuilder.AppendLine(); } for (var columnNumber = 0; columnNumber < Column; columnNumber++) { printBuilder.Append(this[rowNumber, columnNumber].ToString(CultureInfo.InvariantCulture).PadRight(maxLength)); } } return printBuilder.ToString(); } #endregion 转换字符串 }
MathExtensions.cs

/// <summary> /// 扩展出矩阵相关的数学函数。 /// </summary> public static class MathExtensions { /// <summary> /// 矩阵求和。 /// </summary> /// <param name="source">矩阵。</param> /// <returns>和。</returns> public static double Sum(this Matrix source) { double sum = 0; for (var rowNumber = 0; rowNumber < source.Row; rowNumber++) for (var columnNumber = 0; columnNumber < source.Column; columnNumber++) sum += source[rowNumber, columnNumber]; return sum; } /// <summary> /// 矩阵列求和。 /// </summary> /// <param name="source">矩阵。</param> /// <returns>和。</returns> public static Matrix SumColumn(this Matrix source) { var ret = new Matrix(1, source.Column); for (var rowNumber = 0; rowNumber < source.Row; rowNumber++) for (var columnNumber = 0; columnNumber < source.Column; columnNumber++) ret[0, columnNumber] += source[rowNumber, columnNumber]; return ret; } /// <summary> /// 矩阵行求和。 /// </summary> /// <param name="source">矩阵。</param> /// <returns>和。</returns> public static Matrix SumRow(this Matrix source) { var ret = new Matrix(source.Row, 1); for (var rowNumber = 0; rowNumber < source.Row; rowNumber++) for (var columnNumber = 0; columnNumber < source.Column; columnNumber++) ret[rowNumber, 0] += source[rowNumber, columnNumber]; return ret; } /// <summary> /// 对矩阵中的每个元素都进行 Math.Log(x) 运算。 /// </summary> /// <remarks> /// 返回指定数字的自然对数(底为 e)。 /// </remarks> /// <param name="source">矩阵。</param> /// <returns>结果。</returns> public static Matrix Log(this Matrix source) { return source.Function(Math.Log); } /// <summary> /// 对矩阵中的每个元素都进行 Math.Exp(x) 运算。 /// </summary> /// <remarks> /// 即: e 的指定次幂。 /// </remarks> /// <param name="source">矩阵。</param> /// <param name="digits">返回的小数数字(即:该值是 4 的时候,表示保留 4 位小数)。</param> /// <returns>结果。</returns> public static Matrix Exp(this Matrix source, int digits = 0) { if (digits > 0) { return source.Function(item => Math.Round(Math.Exp(item), digits)); } return source.Function(Math.Exp); } /// <summary> /// 对矩阵中的每个元素都进行 Math.Pow(y) 运算。 /// </summary> /// <remarks> /// 即: 指定数字的指定次幂。 /// </remarks> /// <param name="source">矩阵。</param> /// <param name="y">指定次幂。</param> /// <param name="digits">返回的小数数字(即:该值是 4 的时候,表示保留 4 位小数)。</param> /// <returns>结果。</returns> public static Matrix Pow(this Matrix source, int y, int digits = 0) { if (digits > 0) { return source.Function(x => Math.Round(Math.Pow(x, y))); } return source.Function(x => Math.Pow(x, y)); } /// <summary> /// 将双精度浮点值按指定的小数位数舍入。 /// </summary> /// <param name="source">矩阵。</param> /// <param name="digits">返回值中的小数数字。</param> /// <returns>最接近 value 的 digits 位小数的数字矩阵。</returns> public static Matrix Round(this Matrix source, int digits) { return source.Function(item => Math.Round(item, digits)); } /// <summary> /// 对矩阵中的每个元素进行计算。 /// </summary> /// <param name="source">矩阵。</param> /// <param name="func">计算方法。</param> /// <returns>结果。</returns> public static Matrix Function(this Matrix source, Func<double, double> func) { var ret = new Matrix(source.Row, source.Column); for (var rowNumber = 0; rowNumber < source.Row; rowNumber++) for (var columnNumber = 0; columnNumber < source.Column; columnNumber++) ret[rowNumber, columnNumber] = func(source[rowNumber, columnNumber]); return ret; } }
感知器的实现:
注意,在初始化权值(权重)的时候,可以是任意的一个初始值。
Perceptron.cs

/// <summary> /// 感知器。 /// </summary> public class Perceptron { /// <summary> /// 输入参数个数。 /// </summary> private readonly int _inputCount; /// <summary> /// 权重矩阵。 /// </summary> private Matrix _hiddenWeights; /// <summary> /// 初始化感知器。 /// </summary> /// <param name="inputCount">输入参数个数。</param> public Perceptron(int inputCount) { _inputCount = inputCount; //生成输入参数对应的权重。 _hiddenWeights = new Matrix(inputCount, 1, index => -2); } /// <summary> /// 学习率η。 /// </summary> public double Eta => 1; /// <summary> /// 训练。 /// </summary> /// <param name="sample">样本数据。</param> /// <param name="classType">分类。</param> public void Epoch(double[] sample, int classType) { if (sample == null || sample.Length <= 0 || sample.Length != _inputCount) throw new ArgumentException("样本数据不正确"); var matrixSample = new Matrix(1, sample.Length, index => sample[index]); //输出值 y。 var y = Hander(matrixSample); //权重修正。 //w(n + 1) = w(n) + η[d(n) - y(n)]x(n) _hiddenWeights = _hiddenWeights + (Eta * (classType - y) * matrixSample).Transpose(); } #region 计算 /// <summary> /// 真实计算结果。 /// </summary> /// <param name="properties">输入参数。</param> /// <returns>结果。</returns> public double Compute(double[] properties) { if (properties.Length != _inputCount) throw new ArgumentException("输入参数个数不正确"); var matrixProperties = new Matrix(1, properties.Length, index => properties[index]); return Hander(matrixProperties); } #endregion 计算 #region 神经网络处理 public double Hander(Matrix properties) { //诱导局部域 v,_hiddenWeights 矩阵是 1 列,matrixSample 矩阵是 1 行。 //v = x1 * w1+ x2 * w2+···+xm * wm var v = (_hiddenWeights * properties + 1).Sum(); //输出值 y。 var y = 1.0; if (v <= 0) { y = -1.0; } return y; } #endregion 神经网络处理 }
使用示例:

public class PerceptronTest { public static void Execute() { //R1 类的训练样本。 var sample1 = new Matrix(new[] { new[] { 1.0, 2 }, new[] { 2.0, 3 }, new[] { 3.0, 4 } }); //R2 类的训练样本。 var sample2 = new Matrix(new[] { new[] { -1.0, -2 }, new[] { -2.0, -3 }, new[] { -3.0, -4 } }); //定义感知器。 var perceptron = new Perceptron(2); //开始训练。 for (var rowNumber = 0; rowNumber < sample1.Row; rowNumber++) { //这里的输入值是点的坐标,输出值根据公式,当为 R1 类的时候,输出的期望值是 1。 perceptron.Epoch(sample1.GetRow(rowNumber), 1); } for (var rowNumber = 0; rowNumber < sample2.Row; rowNumber++) { //这里的输入值是点的坐标,输出值根据公式,当为 R2 类的时候,输出的期望值是 -1。 perceptron.Epoch(sample2.GetRow(rowNumber), -1); } /* 1.当权值不在改变的时候,就表示训练已完成。 2.当训练完成后,就可以输入任意一个点,自动判断出它是属于哪一类了。 */ var output = perceptron.Compute(new[] { 3.0, 2 }); Console.WriteLine($"点 (3, 2) 是属于 {(output > 0 ? "R1" : "R2")} 类。"); output = perceptron.Compute(new[] { -1.0, -3 }); Console.WriteLine($"点 (-1, -3) 是属于 {(output > 0 ? "R1" : "R2")} 类。"); } }
输出结果:

2.MATLAB 实现
训练函数 Epoch.m
function [output, weights] = Epoch(weights, inputs, target_output, eta)
v = sum(sum(weights * inputs + 1));
y = 1.0;
if v <= 0
y = -1.0;
end
weights = weights + (eta * (target_output - y) * inputs)';
output = y;
end
计算函数 Compute.m
function [ output ] = Compute(inputs, weights)
v = sum(sum(weights * inputs + 1));
y = 1.0;
if v <= 0
y = -1.0;
end
output = y;
end
使用示例 Execute.m
%% Example Title
% 初始化
sample1 = [1,2;2,3;3,4]
sample2 = [-1,-2;-2,-3;-3,-4]
eta = 1
R1 = 1
R2 = -1
weights = [-2;-2]
%% Section 1 Title
% 训练
for index = 1:3
input_sample1 = sample1(index,:);
input_sample2 = sample2(index,:);
[output, weights] = Epoch(weights, input_sample1, R1, eta);
[output, weights] = Epoch(weights, input_sample2, R2, eta);
end
%% Section 2 Title
% 执行计算
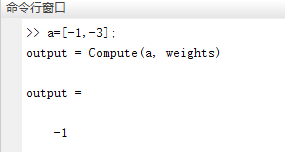
a=[1,3];
output = Compute(a, weights)
输出结果:
R1

R2
参考资料:
《神经网络与机器学习》第三版译本