斜率优化小记

参考资料

斜率优化DP复习笔记 by UntitledCpp

DP的各种优化（动态规划，决策单调性，斜率优化，带权二分，单调栈，单调队列） by FlashHu

下文将以一道例题为引子，描述最简单的斜率优化的一般过程。

P3628 [APIO2010]特别行动队

你有一支由n名士兵组成的部队，士兵从1到n编号，要将他们拆分成若干个特别行动队调入战场。

出于默契的考虑，同一支行动队的队员的编号应该连续。

编号为i的士兵的初始战斗力为xixi，一支行动队的初始战斗力为队内所有队员初始战斗力之和。

通过长期观察，你总结出一支特别行动队的初始战斗力x将按如下公式修正为x’:

\[x′=ax^2+bx+c \]

其中，a,b,c是已知的系数(a<0)。

作为部队统帅，你要为这支部队进行编队，使得所有特别行动队修正后的战斗力之和最大。

试求出这个最大和。

Solution

定义 $f[i]$ 为划分 x1...xi 完毕后能获得的战斗力之和的最大值。

枚举上一个划分点 $j$ ,易得

\[f[i]=\max _{0\leq j \leq i-1} \{f[j]+A*(s[i]-s[j])^2+B*(s[i]-s[j])+C\} \]

单独的考虑 $i$ 以 $j$ 作为决策点的情况。

$f[i]=f[j]+A*(s[i]-s[j])^2+B*(s[i]-s[j])+C$

展开，并按如下规则整理式子：

整理成 $y=kx+b$ 的形式。
所有只含有 $j$ 项和常量放在左边，作为 $y$ 。
所有只含有 $i$ 的项，放在右边，作为 $b$.
只剩余类似 $C \times g(i)\times g(j)$ 的项，把项变到右边，
- $C\times g(i)$ 作为 $k$.
- $g(j)$ 作为 $x$.
如果 $x$ 的表达式单调递减，等式两边同乘 −1 变为单增。

上述规则参考了斜率优化DP复习笔记的有关部分，建议阅读原文。

同时这个步骤和高中的线性规划也有很多相似之处。

整理完毕： $(f[j]+A*s[j]^2-Bs[j]+C)=(2*A*s[i])*s[j]+(f[i]-A*s[i]^2-B*s[i])$.

k已知，那么对于确定的 $j$ , $b$ 也唯一确定。

由于要求 $f[i]$ 的 max ，也就是要让 $b$ （几何意义是截距）最大。

以下是(我假想的) 每个$f[j]$ 对应的点 $(x=s[j],y=f[j]+A*s[j]^2-Bs[j]+C).$ 在平面上的图。

想像一条斜率 $k=2*A*s[i]$ 的直线由上方落下，直到碰上第一个点，取得 $b_{max}.$

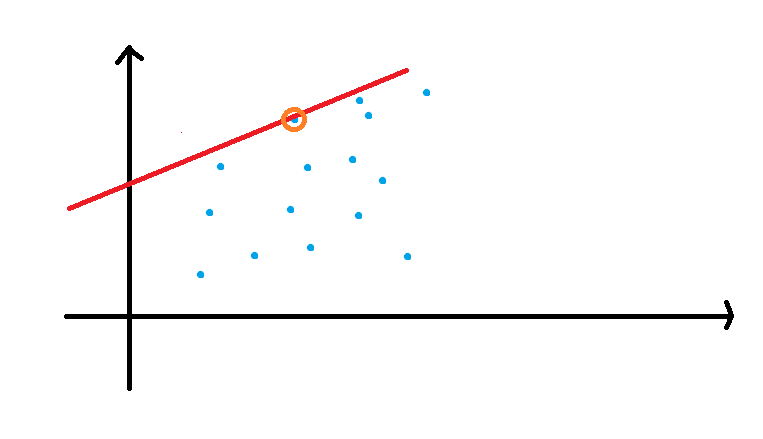
只有上凸包的点有用。

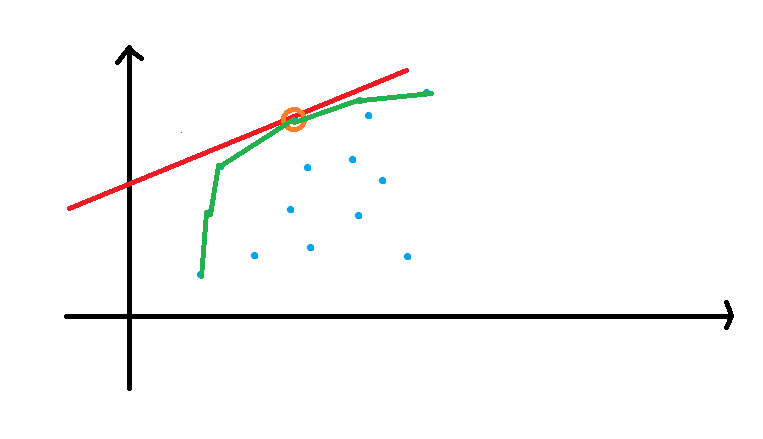
不妨只保留这些点，维护一个上凸包。

每次斜率为 $k$ 的直线只会和上凸包上第一个斜率 $<k$ 的直线碰上。

又观察到本题有特殊的性质，即 $k=2*A*s[i]$ 单调递减，那对于上凸包上斜率 $ \geq k$ 线段，这次碰不上，以后也不会碰到了，所以我们把这些线段删除，直到斜率小于K，取此时的点为决策点进行转移。

把 $i$ 加入决策集合时，如果 $slope(i,q[tt])>slope(q[tt],q[tt-1])$，那么说明 $i $ 在上凸包的上方，$q[tt]$,这个点就没用了，删除并继续。

下面给出Code:

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;
typedef long long LL;
typedef long double LD;
typedef unsigned long long ULL;

const int N=1e6+5;

int n;
LL A,B,C;
LL s[N],f[N];
// f[j]-A*s[j]*s[j]-B*s[j]+C = (2*A*s[i]) * (s[j]) + (f[i]-A*s[i]*s[i]-B*s[i]);
// y=kx+b, k= 2*A*s[i] 单调递减。
// max ---> 维护一个上凸包 ---> 两点斜率单调递减。

inline LD X(int j) { return s[j]; }
inline LD Y(int j) { return f[j]+A*s[j]*s[j]-B*s[j]+C; }
inline bool cmp(int i,int j,int k)
{
    return (Y(j)-Y(i))*(X(k)-X(j))<=(X(j)-X(i))*(Y(k)-Y(j));
}

int q[N];

int main()
{
//  freopen("1.in","r",stdin);
    int i,j;

    scanf("%d%lld%lld%lld",&n,&A,&B,&C);
    for(i=1;i<=n;i++) {
        scanf("%lld",&s[i]);
        s[i]+=s[i-1];
    }

    int hh=0,tt=0;
    q[hh]=0; 
    for(i=1;i<=n;i++) {
        while(hh<tt && Y(q[hh]+1)-Y(q[hh])>=2*A*s[i]*(X(q[hh+1])-X(q[hh]))) hh++;
        j=q[hh]; 
        f[i]=f[j]+A*(s[i]-s[j])*(s[i]-s[j])+B*(s[i]-s[j])+C;
        while(hh<tt&&cmp(q[tt-1],q[tt],i)) tt--;
        q[++tt]=i;
    }

    printf("%lld\n",f[n]);
    return 0;
}

注意事项

斜率的除法变乘法，否则不仅除法的精度不足，而且要特判 $X(i)==X(j)$ 的情况。
注意不等式同乘一个负数要变号。
long double ,有的题会卡这个。但是对于时间限制比较紧的题目，比如运输小猫，用 long double 会 T。
是 hh<tt ,队列中至少要有一个点。

规律

取 $b_{min}$ ---> 下凸包 ---> 斜率为 $k$ 的直线只会和下凸包上第一个斜率 $>k$ 的直线的下端点碰上。
取 $b_{max}$ ---> 上凸包 ---> 斜率为 $k$ 的直线只会和上凸包上第一个斜率 $<k$ 的直线的下端点碰上。

由 $y=kx+b$ 的 $x$ 和 $k$ 的单调情况分类。

1.x单调不降，k单调

有特殊的性质，即 $k$ 单调递减，那对于上凸包上斜率 $ \geq k$ 线段，这次碰不上，以后也不会碰到了，所以我们把这些线段删除，直到斜率小于K，取此时的点为决策点进行转移。

k单调递增同理。

P3628 [APIO2010]特别行动队
P5017 摆渡车
AcWing 301. 任务安排2
AcWing 303. 运输小猫

摆渡车的 Code:

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;
typedef long long LL;
typedef long double LD;
typedef unsigned long long ULL;

const int N=5e6+5;
const LD INF=1e9+5;

int n,m;
int maxt;
int s[N],c[N];
int f[N],ans=INF;

double X(int j) { return c[j]; }
double Y(int j) { return f[j]+s[j]; }
inline bool cmp(int i,int j,int k) 
{
    return (Y(j)-Y(i))*(X(k)-X(j))>=(X(j)-X(i))*(Y(k)-Y(j));
}

int q[N];
int main()
{
//  freopen("1.in","r",stdin);
    int i,j;
    int x;

    cin>>n>>m;
    for(i=1;i<=n;i++) {
        cin>>x,s[x]+=x,c[x]++;
        maxt=max(maxt,x);
    }

    for(i=1;i<=maxt+m;i++) 
        s[i]+=s[i-1],c[i]+=c[i-1];

    memset(f,0x3f,sizeof f);
    f[0]=0;
    int hh=0,tt=0;
    q[hh]=0;
    for (i=1; i<m; i++ ) f[i]=c[i]*i-s[i];
    for(i=m;i<=maxt+m;i++) {
        while(hh<tt&&Y(q[hh])-Y(q[hh+1])>=i*(X(q[hh])-X(q[hh+1]))) hh++;
        j=q[hh];
        f[i]=f[j]+(c[i]-c[j])*i-(s[i]-s[j]);

        j=i+1-m;
        while(hh<tt&&cmp(q[tt-1],q[tt],j)) tt--;
        q[++tt]=j;

        if(i>=maxt) ans=min(ans,f[i]); 
    }
    cout<<ans<<endl;
    return 0;
}

AcWing 301. 任务安排2

#include<cstdio>
#include<cstring>
#include<iostream>

using namespace std;
typedef long long LL;
const int N=3e5+5;

LL f[N];
LL sc[N],st[N],t[N],c[N];
int p[N];
int n;
LL S; 

LL X(int j) { return sc[j]; }
LL Y(int j) { return f[j]-S*sc[j]+sc[n]*S; }
double slope(int i,int j) { return (double)(Y(i)-Y(j))/(X(i)-X(j)); }

int q[N];
int main()
{
//	freopen("1.in","r",stdin);
    int i,j;
    scanf("%d%lld",&n,&S);
    for(i=1;i<=n;i++) {
        scanf("%lld%lld",&t[i],&c[i]);
        sc[i]=sc[i-1]+c[i];
        st[i]=st[i-1]+t[i];
    }
    
    memset(f,0x3f,sizeof f);
    f[0]=0;
    int hh=0,tt=0;
    for(i=1;i<=n;i++) {
        while(hh<tt && slope(q[hh],q[hh+1])<=st[i] ) hh++;
        j=q[hh];
        f[i]=f[j]+(sc[n]-sc[j])*S+(sc[i]-sc[j])*st[i];
        while(hh<tt && slope(q[tt-1],q[tt])>=slope(q[tt],i) ) tt--;
        q[++tt]=i;
    }
    cout<<f[n];
    return 0;
}

运输小猫：

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;
typedef long long LL;
typedef double LD;
typedef unsigned long long ULL;

const int N=1e5+5,P=105;

LL f[N][P]; 

LL d[N],a[N],t[N],s[N];
int h[N];
int q[N];

int n,m,p;
int cur;

inline LD X(int j) { return j; }
inline LD Y(int j) { return f[j][cur]+s[j]; }
inline bool comp(int i,int j,int k)
{
	return (Y(j)-Y(i))*(X(k)-X(j))>=(Y(k)-Y(j))*(X(j)-X(i));
}

int main()
{
//	freopen("1.in","r",stdin);
	int i,j,k;
	scanf("%d%d%d",&n,&m,&p);
	for(i=2;i<=n;i++) {
		scanf("%lld",&d[i]);
		d[i]+=d[i-1];
	}
	for(i=1;i<=m;i++) {
		scanf("%d%lld",&h[i],&t[i]);
		a[i]=t[i]-d[h[i]];
	} 
	sort(a+1,a+m+1);
	for(i=1;i<=m;i++) 
		s[i]=s[i-1]+a[i];
	
	memset(f,0x3f,sizeof f);
	f[0][0]=0;
	int hh,tt;
	for(cur=0,j=1;j<=p;cur++,j++) {
		q[hh=tt=0]=0;
		
		for(i=1;i<=m;i++) {
			while(hh<tt && Y(q[hh+1])-Y(q[hh])<=a[i]*(X(q[hh+1])-X(q[hh]))) hh++;
			k=q[hh];
			f[i][j]=f[k][j-1]+(i-k)*a[i]-s[i]+s[k];
			while(hh<tt && comp(q[tt-1],q[tt],i)) tt--;
			q[++tt]=i;
		}
	}
	
	printf("%lld\n",f[m][p]);
	return 0;
}

2.x单调不降，k不单调

斜率不是递增的，但x单调不降。

所以每次插入时仍从最后插入，但查找决策点需要二分。

P5785 [SDOI2012]任务安排

#include<cstdio>
#include<cstring>
#include<iostream>

using namespace std;
typedef long long LL;

const int N=3e5+5;
const double INF=1e16+5;

LL f[N];
LL sc[N],st[N];
int n;
LL S; 
#define double long double
inline LL X(int j) { return sc[j]; }
inline LL Y(int j) { return f[j]-S*sc[j]+sc[n]*S; }
inline bool cmp(int i,int j,int k) 
{
	return (Y(j)-Y(i))*(X(k)-X(j))>=(X(j)-X(i))*(Y(k)-Y(j));
}
// 斜率 k=st[] 不是递增的，但 x=sc[] 单调不降。
// 所以每次插入时仍从最后插入，但 查找决策点需要二分。

int q[N];

int main()
{
//	freopen("1.in","r",stdin);
    int i,j;
    scanf("%d%lld",&n,&S);
    for(i=1;i<=n;i++) {
        scanf("%lld%lld",&st[i],&sc[i]);
        sc[i]+=sc[i-1];
        st[i]+=st[i-1];
    }
    
    memset(f,0x3f,sizeof f);
    f[0]=0;
    int tt=0,L,R,mid;
    for(i=1;i<=n;i++) {
    	L=-1,R=tt;
    	while(L+1<R) {
			mid=(L+R)>>1;
			if(Y(q[mid+1])-Y(q[mid])<=st[i]*(X(q[mid+1])-X(q[mid]))) L=mid;
			else R=mid;
		}
        j=q[R];

        f[i]=f[j]+(sc[n]-sc[j])*S+(sc[i]-sc[j])*st[i];
        while(tt>0 && cmp(q[tt-1],q[tt],i) ) tt--;
        q[++tt]=i;
    }
    cout<<f[n];
    return 0;
}

3.x不单调

平衡树或 cdq 分治。

posted @ 2020-11-21 14:40 cjlworld 阅读(145) 评论(0) 编辑收藏举报

刷新页面返回顶部

cjlworld

三千里追云逐月，只为金乌一瞥；八万场刀光剑影，终究卸甲归田。

斜率优化小记

P3628 [APIO2010]特别行动队

Solution

1.x单调不降，k单调

2.x单调不降，k不单调

3.x不单调

公告

cjlworld

三千里追云逐月，只为金乌一瞥； 八万场刀光剑影，终究卸甲归田。

斜率优化小记

P3628 [APIO2010]特别行动队

Solution

1.x单调不降，k单调

2.x单调不降，k不单调

3.x不单调

公告

三千里追云逐月，只为金乌一瞥；八万场刀光剑影，终究卸甲归田。