在平衡树的海洋中畅游（一）——Treap

记得有一天翔哥毒奶我们：

当你们已经在平衡树的海洋中畅游时，我还在线段树的泥沼中挣扎。

我觉得其实像我这种对平衡树一无所知的蒟蒻也要开一开数据结构了。

然后花了一天啃了下最简单的平衡树Treap，感觉还是可以接受的。

下一步争取把Splay和替罪羊树给nāng下来。至于SB-tree还是算了吧。

首先我们要知道Treap为什么要叫Treap，这很简单：

Treap=Tree+heap（树+堆）

我们类比于一般的BST，它们都有一些共同的特点：

1. 都是二叉树的结构
2. 对于所有的非叶子节点，它的左儿子（如果有的话）的值都严格小于它，它的右儿子（如果有的话）的值都严格大于它。

很显然，期望情况下树的高度就是\(log\)级别的了。然后一次操作的复杂度就是\(O(log\ n)\)的

然后对于普通的BST，就有一个致命的弱点了。让数据为一条链时，那么树的高度就变成\(n\)的了。

所以我们就要让树的高度尽量平衡，于是我们想当：当数据随机排列是这个数高就是\(log\)级别的了。

但是数据是不可能重新排列的，但我们可以手动调整树的形状，并且只要在基于随机的基础上就可以了。然后就有了Treap。

Treap的基本思想也建立于此，我们在刚开始给每个节点随机一个值。然后对于这棵树在保持BST性质的同时还要保持堆的性质，这里我一般采用大根堆的性质。

然后就有一个问题了。我们按BST的性质插入后，如何维护堆的性质？

然后就是整个Treap中（也是Splay中）最难的操作了——旋转！

我们先放一张经典的图：

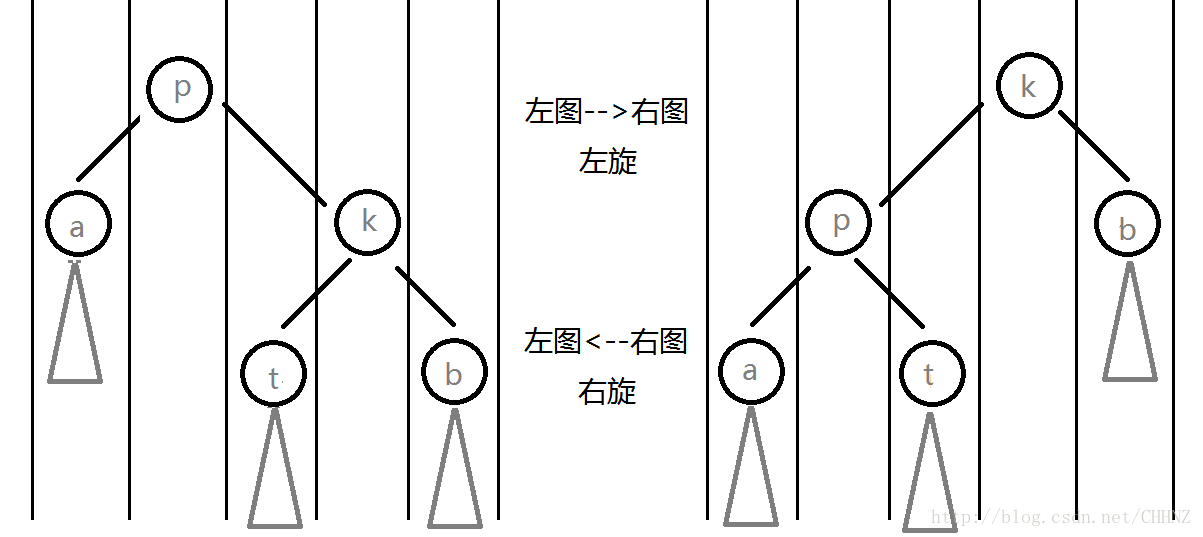
所谓左旋就是逆时针，右旋为顺时针。向上面那样，旋转之后，节点的左右位置不变，即BST性质不变，而p与k的上下位置变化了，a和b的深度也发生变化了。通过旋转，我们也可以在不破坏BST性质的前提下维护堆性质。

然后我们就只要在插入和删除时通过旋转维护堆性质即可。

然后我们结合一道模板题P3369 【模板】普通平衡树（Treap/SBT）来具体讲解一下Treap的操作（代码有注释）

#include<cstdio>
using namespace std;
const int N=100005,INF=1e9;
struct treap
{
    int val,dat,size,cnt,ch[2];
}node[N];//Treap的节点信息
//val表示数的值，dat表示rand()出来的优先级，size是子树大小，cnt是一个点的重复的个数，ch[]表示的是左右儿子的编号，由于没有用指针，请大家注意一下下面的很多操作都是要加'&'的
int m,opt,x,rt,tot;
inline char tc(void)
{
    static char fl[100000],*A=fl,*B=fl;
    return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0; char ch=tc(); int flag=1;
    while (ch<'0'||ch>'9') { if (ch=='-') flag=-1; ch=tc(); }
    while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc(); x*=flag;
}
inline void write(int x)
{
    if (x<0) putchar('-'),x=-x;
    if (x>9) write(x/10);
    putchar(x%10+'0');
}
inline int rand() //加速的手写rand()函数，那个玄学的取值我也不知道是什么鬼。
{
    static int seed=233;
    return seed=(int)seed*482711LL%2147483647; 
}
inline void pushup(int rt)//类似于线段树的更新，注意不要忘记把自身的副本数加上
{
    node[rt].size=node[node[rt].ch[0]].size+node[node[rt].ch[1]].size+node[rt].cnt;
}
inline int build(int v)//建立新的节点，返回节点编号
{
    node[++tot].val=v; node[tot].dat=rand();
    node[tot].size=node[tot].cnt=1; return tot;
}
inline void init(void)//初始化，防止后面的一些操作出现越界错误（不用指针就是有些问题）
{
    rt=build(-INF); node[rt].ch[1]=build(INF); pushup(rt);
}
inline void rotate(int &rt,int d)//旋转，0表示左旋，1表示右旋
{
    int temp=node[rt].ch[d^1]; node[rt].ch[d^1]=node[temp].ch[d]; node[temp].ch[d]=rt; //这里注意修改的顺序，强烈建议自己手动画图理解一下
    rt=temp; pushup(node[rt].ch[d]); pushup(rt);
}
inline void insert(int &rt,int v)//插入一个值为v的数
{
    if (!rt) { rt=build(v); return; }
    if (v==node[rt].val) ++node[rt].cnt; else //注意重复的节点处理方法
    {
        int d=v<node[rt].val?0:1; insert(node[rt].ch[d],v);//SBT的性质
        if (node[node[rt].ch[d]].dat>node[rt].dat) rotate(rt,d^1);//如果违反就旋转，注意这里的d要^1（结合旋转方向理解一下即可）
    }
    pushup(rt);
}
inline void remove(int &rt,int v)
{
    if (!rt) return;
    if (v==node[rt].val)
    {
        if (node[rt].cnt>1) { --node[rt].cnt; pushup(rt); return; }
        if (node[rt].ch[0]||node[rt].ch[1])//如果这个节点有子树就要旋到叶节点再删除
        {
            if (!node[rt].ch[1]||node[node[rt].ch[0]].dat>node[node[rt].ch[1]].dat) rotate(rt,1),remove(node[rt].ch[1],v);
            else rotate(rt,0),remove(node[rt].ch[0],v); pushup(rt);
        } else rt=0; return;//这里是对于所有删除情况的结束
    }
    if (v<node[rt].val) remove(node[rt].ch[0],v); else remove(node[rt].ch[1],v); pushup(rt);//同样要符合SBT的性质
}
inline int get_rank(int &rt,int v)//查询v的排名
{
    if (!rt) return 0;
    if (v==node[rt].val) return node[node[rt].ch[0]].size+1; else//相等就返回子树大小+1
    if (v<node[rt].val) return get_rank(node[rt].ch[0],v); else//小于就在左子树中找
    return node[node[rt].ch[0]].size+node[rt].cnt+get_rank(node[rt].ch[1],v);//大于在右子树中找，注意这里要减去那一部分
}
inline int get_val(int &rt,int rk)//查询排名为rk的数
{
    if (!rt) return INF;//道理基本同上
    if (rk<=node[node[rt].ch[0]].size) return get_val(node[rt].ch[0],rk); else
    if (rk<=node[node[rt].ch[0]].size+node[rt].cnt) return node[rt].val; else //注意这里不要忽略副本的多少
    return get_val(node[rt].ch[1],rk-node[node[rt].ch[0]].size-node[rt].cnt);
}
inline int get_pre(int &rt,int v)//找前驱
{
    int now=rt,pre;
    while (now)//个人感觉迭代的比递归好些
    {
        if (node[now].val<v) pre=node[now].val,now=node[now].ch[1];//这里要注意，如果当前点的值小于目标那么总是到右子树去找（有点贪心的思想）
        else now=node[now].ch[0];
    }
    return pre;
}
inline int get_next(int &rt,int v)//找后继，原理同上
{
    int now=rt,next;
    while (now)
    {
        if (node[now].val>v) next=node[now].val,now=node[now].ch[0];
        else now=node[now].ch[1];
    }
    return next;
}
int main()
{
    //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
    read(m); init();
    while (m--)
    {
        read(opt); read(x);
        switch (opt)
        {
            case 1:insert(rt,x); break;
            case 2:remove(rt,x); break;
            case 3:write(get_rank(rt,x)-1),putchar('\n'); break; //注意这里由于我们刚开始是加入了两个放溢出的节点，因此要-1。下面同理
            case 4:write(get_val(rt,x+1)),putchar('\n'); break;
            case 5:write(get_pre(rt,x)),putchar('\n'); break;
            case 6:write(get_next(rt,x)),putchar('\n'); break;
        }
    }
    return 0;
}

其中Treap还有类似于堆的功能，可以求出Treap中的最大（小）值

具体实现很简单，由于SBT的性质，所以我们一直从左子树（找最小值时）或右子树（找最大值时）一路找到叶子节点即可，这里我们结合一道板子题POJ3481来看一下吧

CODE

#include<cstdio>
using namespace std;
const int N=1e6+5;
struct Treap
{
	int val,dat,num,ch[2];
}node[N];
int opt,k,x,rt,tot,now,size;
inline char tc(void)
{
	static char fl[100000],*A=fl,*B=fl;
	return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
	x=0; char ch=tc(); int flag=1;
	while (ch<'0'||ch>'9') { if (ch=='-') flag=-1; ch=tc(); }
	while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc(); x*=flag;
}
inline void write(int x)
{
	if (x<0) putchar('-'),x=-x;
	if (x>9) write(x/10);
	putchar(x%10+'0');
}
inline int rand(void) 
{
    static int seed=233;
    return seed=(int)seed*482711LL%2147483647; 
}
inline int build(int v,int num)
{
	node[++tot].val=v; node[tot].dat=rand(); node[tot].num=num; return tot;
}
inline void rotate(int &rt,int d)
{
	int temp=node[rt].ch[d^1]; node[rt].ch[d^1]=node[temp].ch[d];
	node[temp].ch[d]=rt; rt=temp;
}
inline void insert(int &rt,int v,int num)
{
	if (!rt) { rt=build(v,num); return; }
	int d=v<node[rt].val?0:1; insert(node[rt].ch[d],v,num);
	if (node[rt].dat<node[node[rt].ch[d]].dat) rotate(rt,d^1);
}
inline void remove(int &rt,int v)
{
	if (!size) return;
	if (v==node[rt].val)
	{
		if (node[rt].ch[0]||node[rt].ch[1])
		{
			if (!node[rt].ch[1]||node[node[rt].ch[0]].dat>node[node[rt].ch[1]].dat) rotate(rt,1),remove(node[rt].ch[1],v);
			else rotate(rt,0),remove(node[rt].ch[0],v);
		} else rt=0; return;
	}
	if (v<node[rt].val) remove(node[rt].ch[0],v); else remove(node[rt].ch[1],v);
}
inline int get_min(int rt)
{
	if (!size) return 0;
	while (node[rt].ch[0]) rt=node[rt].ch[0];
	now=node[rt].val; return node[rt].num;
}
inline int get_max(int rt)
{
	if (!size) return 0;
	while (node[rt].ch[1]) rt=node[rt].ch[1];
	now=node[rt].val; return node[rt].num;
}
int main()
{
	//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
	for (;;)
	{
		read(opt); if (!opt) break;
		switch (opt)
		{
			case 1:read(k),read(x),insert(rt,x,k),++size; break;
			case 2:write(get_max(rt)),putchar('\n'),size&&(remove(rt,now),--size); break;
			case 3:write(get_min(rt)),putchar('\n'),size&&(remove(rt,now),--size); break;
		}
	}
	return 0;
}