The 1st Universal Cup. Stage 8: Slovenia
Preface
这场其实是昨天打的,但因为今天没训练就摆烂拖到今天才补题和写博客
这场题感觉都挺可做的,但前期出题有点慢导致后期没时间了,徐神和祁神赛后 20min 过了 J 有点可惜
A. Bandits
题都没看,不做评价
B. Combination Locks
不难发现这题本质就是在 0/1 串上操作,每次移动到另一个与之汉明距离为 \(1\) 的串
考虑把图建出来,不难发现这是个二分图,即根据状态中 \(1\) 的个数的奇偶性将点分为了两类
二分图上的博弈算是个经典问题,只要看起点是否在最大匹配上即可,具体证明可以看 这里
#include<cstdio>
#include<iostream>
#include<vector>
#define RI register int
#define CI const int&
using namespace std;
const int N=(1<<10)+5;
int t,n,m,ban[N],vis[N],pre[N]; char A[N],B[N]; vector <int> v[N];
inline int find(CI now,CI idx)
{
for (auto to:v[now])
{
if (vis[to]==idx) continue; vis[to]=idx;
if (pre[to]==-1||find(pre[to],idx)) return pre[to]=now,1;
}
return 0;
}
inline int work(void)
{
for (RI mask=0;mask<(1<<n);++mask)
{
v[mask].clear();
if (__builtin_popcount(mask)%2==1) continue;
if (ban[mask]) continue;
for (RI i=0;i<n;++i)
{
int nxt=mask^(1<<i);
if (ban[nxt]) continue;
v[mask].push_back(nxt);
//printf("%d -> %d\n",mask,nxt);
}
}
int match=0,idx=0;
for (RI i=0;i<(1<<n);++i) vis[i]=pre[i]=-1;
for (RI mask=0;mask<(1<<n);++mask)
{
if (__builtin_popcount(mask)%2==1) continue;
if (ban[mask]) continue;
match+=find(mask,++idx);
}
return match;
}
int main()
{
for (scanf("%d",&t);t;--t)
{
scanf("%d%d",&n,&m);
for (RI i=0;i<(1<<n);++i) ban[i]=0;
scanf("%s%s",A,B); int st=0;
for (RI i=0;i<n;++i) if (A[i]==B[i]) st|=(1<<i);
for (RI i=1;i<=m;++i)
{
scanf("%s",A); int mask=0;
for (RI j=0;j<n;++j) if (A[j]=='=') mask|=(1<<j);
ban[mask]=1;
}
int pre_match=work();
//printf("pre = %d\n",pre_match);
ban[st]=1;
int alt_match=work();
//printf("alt = %d\n",alt_match);
puts(pre_match!=alt_match?"Alice":"Bob");
}
return 0;
}
C. Constellations
祁神和徐神中期开的,当时我在想 B 所以题都没看
#include<bits/stdc++.h>
using namespace std;
#define int long long
struct Pt{
int x, y;
Pt operator-(const Pt &b)const{return Pt{x-b.x, y-b.y};}
int len2()const{return x*x+y*y;}
};
const int N = 4005;
int n;
Pt pt[N];
int dis[N][N], sz[N], tot;
bool del[N];
struct Node{
int u, v;
bool operator>(const Node &b)const{
int res1 = dis[u][v] * sz[b.u]*sz[b.v];
int res2 = dis[b.u][b.v] * sz[u]*sz[v];
if (res1 != res2) return res1 < res2;
else return (u!=b.u ? u<b.u : v<b.v);
}
bool operator<(const Node &b)const{return b > (*this);}
};
signed main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n;
tot = n;
for (int i=1; i<=n; ++i){
cin >> pt[i].x >> pt[i].y;
sz[i] = 1;
}
priority_queue<Node> Q;
for (int i=1; i<=n; ++i) for (int j=i+1; j<=n; ++j) dis[i][j] = dis[j][i] = (pt[i]-pt[j]).len2();
for (int i=1; i<=n; ++i) for (int j=i+1; j<=n; ++j) Q.push(Node{i, j});
while (!Q.empty()){
auto [u, v] = Q.top(); Q.pop();
if (del[u] || del[v]) continue;
del[u] = del[v] = true;
int x = ++tot;
sz[x] = sz[u]+sz[v];
for (int i=1; i<tot; ++i) if (!del[i]) {
dis[i][x] = dis[x][i] = dis[u][i]+dis[v][i];
Q.push(Node{i, x});
}
cout << sz[x] << '\n';
}
return 0;
}
D. Deforestation
难点在于阅读题意
仔细看题后发现在某个点处最多只能将子节点打包一次,因此贪心地将最小的子节点打包即可
#include<cstdio>
#include<iostream>
#include<vector>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
int W,ans;
inline int DFS(void)
{
int x,y; scanf("%d%d",&x,&y);
vector <int> vec(y);
for (RI i=0;i<y;++i)
{
int tmp=DFS(); ans+=tmp/W; vec[i]=tmp%W;
}
sort(vec.begin(),vec.end());
int sum=0;
for (RI i=0;i<y;++i)
if (sum+vec[i]<=W) sum+=vec[i]; else ++ans;
return x+sum;
}
int main()
{
scanf("%d",&W);
ans+=(DFS()+W-1)/W;
return printf("%d",ans),0;
}
E. Denormalization
这题也是祁神和徐神开出来的,我题意都不知道
#include<bits/stdc++.h>
using namespace std;
using LD = double;
const int N = 1e4+5;
const LD eps = 5e-7;
int n, r[N], ans[N];
LD A[N], rt[N];
int gcd(int a, int b){return 0==b ? a : gcd(b, a%b);}
LD check(){
int64_t d = 0;
for (int i=1; i<=n; ++i) d += r[i]*r[i];
LD dt = sqrt(d);
for (int i=1; i<=n; ++i) rt[i] = r[i]/dt;
LD res = 0;
for (int i=1; i<=n; ++i){
res = max(abs(rt[i] - A[i]), res);
}
return res;
}
signed main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n;
int mx=1;
for (int i=1; i<=n; ++i){
cin >> A[i];
if (A[i] > A[mx]) mx=i;
}
LD minv = 1e30;
for (int i=1; i<=10000; ++i){
LD res = i / A[mx];
for (int j=1; j<=n; ++j) r[j] = round(A[j]*res);
LD rs = check();
if(rs < minv) minv = rs, memcpy(ans, r, sizeof(int) * (n + 1));
// std::cerr << r[mx] << ' ' << rs << char(10);
}
// std::cerr << "Error = " << minv << char(10);
int g = ans[1];
for(int i=1; i<=n; ++i) g = __gcd(g, ans[i]);
for (int i=1; i<=n; ++i){
cout << ans[i] / g << '\n';
}
return 0;
}
F. Differences
赛时一直在想随机化之类的神秘东西,中间一度想到 Hash 但没想到转化,最后也是不了了之
考虑枚举答案串 \(S_x\),考虑如何检验,我们可以尝试维护一个数组 \(\{d\}\),其中 \(d_i\) 表示第 \(i\) 个串与 \(S_x\) 的汉明距离
考虑枚举 \(S_x\) 每一位上的字符,若当前位为 A,则显然当前位为 \(B,C,D\) 的这些串对应的 \(\{d\}\) 位置上要加一
用 Hash 维护 \(\{d\}\) 数组即可,复杂度 \(O(nm)\)
#include<cstdio>
#include<iostream>
#include<string>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
const int mod1=998244353,mod2=1e9+7;
struct Hasher
{
int x,y;
inline Hasher(CI X=0,CI Y=0)
{
x=X; y=Y;
}
friend inline bool operator == (const Hasher& A,const Hasher& B)
{
return A.x==B.x&&A.y==B.y;
}
friend inline Hasher operator + (const Hasher& A,const Hasher& B)
{
return Hasher((A.x+B.x)%mod1,(A.y+B.y)%mod2);
}
friend inline Hasher operator - (const Hasher& A,const Hasher& B)
{
return Hasher((A.x-B.x+mod1)%mod1,(A.y-B.y+mod2)%mod2);
}
friend inline Hasher operator * (const Hasher& A,const Hasher& B)
{
return Hasher(1LL*A.x*B.x%mod1,1LL*A.y*B.y%mod2);
}
}pw[N],f[N][4];
int n,m,k; string s[N];
const Hasher seed=Hasher(31,131);
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin>>n>>m>>k;
pw[0]=Hasher(1,1); for (RI i=1;i<=n;++i) pw[i]=pw[i-1]*seed;
Hasher all_f,all_k;
for (RI i=1;i<=n;++i)
{
cin>>s[i];
for (RI j=0;j<m;++j)
f[j][s[i][j]-'A']=f[j][s[i][j]-'A']+pw[i];
}
for (RI i=0;i<m;++i) for (RI j=0;j<4;++j) all_f=all_f+f[i][j];
for (RI i=1;i<=n;++i) all_k=all_k+pw[i]*Hasher(k,k);
for (RI i=1;i<=n;++i)
{
Hasher cur=all_f;
for (RI j=0;j<m;++j) cur=cur-f[j][s[i][j]-'A'];
if (cur==all_k-pw[i]*Hasher(k,k)) return cout<<i,0;
}
return 0;
}
G. Greedy Drawers
唉构造,后期徐神和祁神都去开 J 了,留我一个构造苦手看 G,最后也是啥也每构造出来
看了一眼题解只能说是巧妙,其实就是构造如下的子结构,使得红色的点有 \(\frac{1}{2}\) 的概率选错
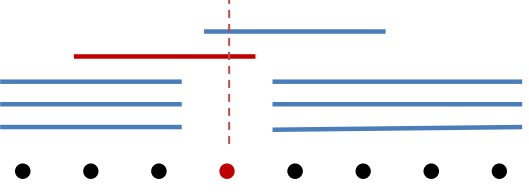
而具体构造时,我们可以令编号为 \(i\) 的物品的长宽为 \((i,2n-i)\)
此时长宽为 \((r,2n-l)\) 的抽屉就恰好可以 cover 编号 \(\in[l,r]\) 的物品,要构造上图的 Case 就很简单了,最后重复多次这种子结构即可
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
int n;
int main()
{
scanf("%d",&n);
for (RI i=1;i<=n;++i) printf("%d %d\n",i,2*n-i);
putchar('\n');
auto cover=[&](CI l,CI r)
{
printf("%d %d\n",r,2*n-l);
};
int st=0; while (st+8<=n)
{
for (RI i=0;i<3;++i) cover(st+1,st+3),cover(st+5,st+8);
cover(st+2,st+4); cover(st+4,st+6); st+=8;
}
while (st<n) cover(st+1,st+1),++st;
return 0;
}
H. Insertions
题都没看,不做评价
I. Money Laundering
题都没看,不做评价
J. Mortgage
经典动态凸壳,一般这种题我就看个乐呵
不难发现将每个位置的前缀和数组求出后,就变成求一段区间内和一个该区间左端点的斜率最小值
从右往左扫描线,不难发现待选点构成了一段凸壳,但众所周知凸壳插入容易删除难,这题还有变化的右端点要处理
解决方法也很经典,用树状数组维护凸壳,询问的时候在每个节点处三分/二分出最优值即可,总复杂度 \(O(m\log^2 n)\)
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+5;
int n, m, A[N], sum[N];
struct Node{
int R, id;
bool operator<(const Node &b)const{return R!=b.R ? R>b.R : id<b.id;}
};
vector<Node> qry[N];
int ans[N];
struct Convh{
vector<int> stk; int sz=0;
void add(int id){
while (sz>1 &&
(sum[stk[sz-1]]-sum[id])*(stk[sz-2]-stk[sz-1]) >
(sum[stk[sz-2]]-sum[stk[sz-1]])*(stk[sz-1]-id))
stk.pop_back(), --sz;
stk.push_back(id); ++sz;
}
int find(int id){
int L=0, R=sz-1;
while (R - L > 20){
int M1 = L+(R-L)/2, M2 = M1+1;
int res1 = (sum[stk[M1]]-sum[id])*(stk[M2]-id);
int res2 = (sum[stk[M2]]-sum[id])*(stk[M1]-id);
if (res1 == res2) L=R;
else if (res1 < res2) R = M2;
else L = M1;
// std::cerr << "FUCK\n";
}
int ans = 0x7f7f7f7f;
while(L <= R) {
if(sum[stk[L]]-sum[id] < 0) return -1;
else ans = min(ans, (sum[stk[L]]-sum[id])/(stk[L]-id)), L++;
}
if (ans>=0) return ans;
else return -1;
}
};
Convh c[N];
signed main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m;
for (int i=1; i<=n; ++i) cin >> A[i], sum[i] = sum[i-1]+A[i];
for (int i=1; i<=m; ++i){
int s, k; cin >> s >> k;
qry[s-1].push_back(Node{s+k-1, i});
}
for (int i=0; i<n; ++i) sort(qry[i].begin(), qry[i].end());
for (int i=n; i>=0; --i){
for(auto [q, id]: qry[i]) {
int l = i + 1, r = q + 1, a = 0x7f7f7f7f;
for(int j = r; j; j -= j&-j) if(c[j].sz) a = std::min(a, c[j].find(l - 1));
ans[id] = a;
}
for(int j = i + 1; j <= n + 1; j += j&-j) c[j].add(i);
}
for(int i = 1; i <= m; ++i) {
if(ans[i] < 0) std::cout << "stay with parents\n";
else std::cout << ans[i] << char(10);
}
return 0;
}
K. Skills in Pills
不难发现可以假设允许一天吃两片药,这样在 \(\operatorname{LCM}(k,j)\) 那天会出现冲突
要解决冲突实际上就是将某片药的时间提前一天即可,刚开始想着贪心提前间隔更小的药,后面手玩了下发现样例都过不去
遂决定直接大力 DP,令 \(f_i\) 表示到了第 \(i\) 天,且此时在第 \(i\) 天恰好有冲突时最少要吃几片药
转移分两种情况讨论下即可,两种情况的贡献可以提前预处理出来,总复杂度 \(O(n)\)
#include<cstdio>
#include<iostream>
#include<algorithm>
#define int long long
#define RI register int
#define CI const int&
using namespace std;
const int N=1e6+5,INF=1e9;
int n,A,B,f[N],x_1,y_1,x_2,y_2,ans;
signed main()
{
scanf("%lld%lld%lld",&A,&B,&n);
int lcm=A*B/__gcd(A,B);
if (n<lcm) return printf("%lld",n/A+n/B),0;
for (RI i=0;i<=n;++i) f[i]=INF; ans=INF;
f[lcm]=lcm/A+lcm/B;
x_1=y_1=-1;
for (RI i=1;B*i+1<=n;++i)
if ((B*i+1)%A==0) { x_1=(B*i+1)/A; y_1=i; break; }
x_2=y_2=-1;
for (RI i=1;A*i+1<=n;++i)
if ((A*i+1)%B==0) { y_2=(A*i+1)/B; x_2=i; break; }
for (RI i=lcm;i<=n;++i)
{
if (f[i]==INF) continue;
if (x_1!=-1&&i+B*y_1<=n) f[i+B*y_1]=min(f[i+B*y_1],f[i]+x_1+y_1);
else ans=min(ans,f[i]+(n-i)/B+(n-i+1)/A);
if (x_2!=-1&&i+A*x_2<=n) f[i+A*x_2]=min(f[i+A*x_2],f[i]+x_2+y_2);
else ans=min(ans,f[i]+(n-i)/A+(n-i+1)/B);
}
return printf("%lld",ans),0;
}
L. The Game
题意看懂就随便写的模拟题,代码看起来挺长其实中间一大段都是赋值粘贴的,其实想清楚了很好写
#include<cstdio>
#include<iostream>
#include<vector>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
int main()
{
//freopen("ex_tests_2.in","r",stdin); freopen("my.ans","w",stdout);
vector <int> pile,hand,row[4];
row[0].push_back(1); row[1].push_back(1);
row[2].push_back(100); row[3].push_back(100);
for (RI i=2;i<=99;++i)
{
int x; scanf("%d",&x); pile.push_back(x);
}
reverse(pile.begin(),pile.end());
for (RI i=1;i<=8;++i) hand.push_back(pile.back()),pile.pop_back();
for (;!hand.empty();)
{
{
int back_trick=-1,row_id=-1;
for (RI i=0;i<hand.size();++i)
{
int x=hand[i];
if (row[0].back()>x&&row[0].back()==x+10)
{
back_trick=i; row_id=0; break;
}
if (row[1].back()>x&&row[1].back()==x+10)
{
back_trick=i; row_id=1; break;
}
if (row[2].back()<x&&row[2].back()==x-10)
{
back_trick=i; row_id=2; break;
}
if (row[3].back()<x&&row[3].back()==x-10)
{
back_trick=i; row_id=3; break;
}
}
if (back_trick!=-1)
{
row[row_id].push_back(hand[back_trick]);
hand.erase(hand.begin()+back_trick);
} else
{
int hand_id=-1,dlt=1e9,row_id=-1;
for (RI i=0;i<hand.size();++i)
{
int x=hand[i],cur_dlt=1e9,cur_id=-1;
if (row[0].back()<x)
{
if (x-row[0].back()<cur_dlt) cur_dlt=x-row[0].back(),cur_id=0;
}
if (row[1].back()<x)
{
if (x-row[1].back()<cur_dlt) cur_dlt=x-row[1].back(),cur_id=1;
}
if (row[2].back()>x)
{
if (row[2].back()-x<cur_dlt) cur_dlt=row[2].back()-x,cur_id=2;
}
if (row[3].back()>x)
{
if (row[3].back()-x<cur_dlt) cur_dlt=row[3].back()-x,cur_id=3;
}
if (cur_dlt<dlt) hand_id=i,dlt=cur_dlt,row_id=cur_id;
}
if (hand_id==-1) break;
row[row_id].push_back(hand[hand_id]);
hand.erase(hand.begin()+hand_id);
}
}
{
int back_trick=-1,row_id=-1;
for (RI i=0;i<hand.size();++i)
{
int x=hand[i];
if (row[0].back()>x&&row[0].back()==x+10)
{
back_trick=i; row_id=0; break;
}
if (row[1].back()>x&&row[1].back()==x+10)
{
back_trick=i; row_id=1; break;
}
if (row[2].back()<x&&row[2].back()==x-10)
{
back_trick=i; row_id=2; break;
}
if (row[3].back()<x&&row[3].back()==x-10)
{
back_trick=i; row_id=3; break;
}
}
if (back_trick!=-1)
{
row[row_id].push_back(hand[back_trick]);
hand.erase(hand.begin()+back_trick);
} else
{
int hand_id=-1,dlt=1e9,row_id=-1;
for (RI i=0;i<hand.size();++i)
{
int x=hand[i],cur_dlt=1e9,cur_id=-1;
if (row[0].back()<x)
{
if (x-row[0].back()<cur_dlt) cur_dlt=x-row[0].back(),cur_id=0;
}
if (row[1].back()<x)
{
if (x-row[1].back()<cur_dlt) cur_dlt=x-row[1].back(),cur_id=1;
}
if (row[2].back()>x)
{
if (row[2].back()-x<cur_dlt) cur_dlt=row[2].back()-x,cur_id=2;
}
if (row[3].back()>x)
{
if (row[3].back()-x<cur_dlt) cur_dlt=row[3].back()-x,cur_id=3;
}
if (cur_dlt<dlt) hand_id=i,dlt=cur_dlt,row_id=cur_id;
}
if (hand_id==-1) break;
row[row_id].push_back(hand[hand_id]);
hand.erase(hand.begin()+hand_id);
}
}
if (!pile.empty())
{
hand.push_back(pile.back()); pile.pop_back();
hand.push_back(pile.back()); pile.pop_back();
}
}
for (RI i=0;i<4;++i)
{
for (auto x:row[i]) printf("%d ",x); putchar('\n');
}
for (auto x:hand) printf("%d ",x); putchar('\n');
reverse(pile.begin(),pile.end());
for (auto x:pile) printf("%d ",x); putchar('\n');
return 0;
}
Postscript
明天最后训一场暑假就结束了,也是成为大三老登了,希望最后一个赛季不留遗憾吧


 浙公网安备 33010602011771号
浙公网安备 33010602011771号