Pinely Round 1 (Div. 1 + Div. 2)
Preface
其实这场上周一就补了ABC,但是由于各种事情的堆积一直到今天才开始接着补D
再不写博客的话可能题意都要忘光光了,赶紧来Rush一发
A. Two Permutations
简单观察发现,如果\(a+b\ge n-1\),则两段有交集(或中间仅存在一个数)必然不合法,否则总能构造出一种合法解
但是要注意特判\(a=n\and b=n\)的情形
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
int t,n,a,b;
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
scanf("%d%d%d",&n,&a,&b);
if (a==n&&b==n) { puts("Yes"); continue; }
if (n-(a+b)<=1) puts("No"); else puts("Yes");
}
return 0;
}
B. Elimination of a Ring
补题的时候光速看出结论秒了,结果现在写博客的时候对着我原来的代码想了半天才搞懂
我们发现若序列是\(A-B-A-B-\cdots-A-B\)这样的模式,那么每次操作一定会导致相邻的两个兑掉,因此答案就是\(\frac{n}{2}+1\)
否则我们总可以找到一种方案使得答案为\(n\),具体地,此时肯定存在不同于\(A,B\)的数\(C\)
我们每次都选择和\(C\)相邻的且不会导致两个\(C\)兑掉的数进行操作即可保证取得这个上界
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=105;
int t,n,a[N]; bool c[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d",&n),i=0;i<n;++i) scanf("%d",&a[i]);
if (n==1) { puts("1"); continue; }
for (i=0;i<n;++i) c[i]=a[(i-1+n)%n]==a[(i+1)%n];
bool flag=0; for (i=0;i<n&&!flag;++i) if (!c[i]) flag=1;
if (flag) printf("%d\n",n); else printf("%d\n",n/2+1);
}
return 0;
}
C. Set Construction
大力乱搞之后我们很容易得到一种构造方案:
-
初始时令每个点\(i\)的集合为\(\{i\}\),考虑若\(s_{i,j}=1\),则连一条\(i\to j\)的边
-
对这个图作拓扑排序,每次把一个点的集合内的所有点扔到它的下一个点里
不难发现这样构造的图是一定满足条件的
#include<cstdio>
#include<set>
#include<vector>
#define RI register int
#define CI const int&
using namespace std;
const int N=105;
int t,n,in[N],q[N]; char g[N]; vector <int> v[N]; set <int> s[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i,j; for (scanf("%d",&n),i=1;i<=n;++i)
for (s[i].clear(),s[i].insert(i),v[i].clear(),in[i]=0,scanf("%s",g+1),j=1;j<=n;++j)
if (g[j]=='1') v[i].push_back(j),++in[j];
RI H=0,T=0; for (i=1;i<=n;++i) if (!in[i]) q[++T]=i;
while (H<T)
{
int now=q[++H]; for (int to:v[now])
{
for (int x:s[now]) s[to].insert(x);
if (!--in[to]) q[++T]=to;
}
}
for (i=1;i<=n;++i)
{
printf("%d ",s[i].size());
for (int x:s[i]) printf("%d ",x); putchar('\n');
}
}
return 0;
}
D. Carry Bit
想了半天结果情况没分好寄了,又被简单计数题虐了呜呜呜(我发现现在我做数数题就是思路都有但总是划分不好状态)
我们发现\(a+b\)在二进制下的每一次进位都会导致\(f(a,b)\)加\(1\),因此题目等价于求产生\(k\)次进位的方案数
考虑进位操作存在连续性,具体地,设\(A\)表示二进制下这一位产生了进位,\(B\)表示二进制下这一位不进位
则这\(n\)位的形式一定是形如\(AABBBBABBA\)这样的(开头可以是\(A\)也可以是\(B\),结尾同理,这里只是表示下形式)
并且我们发现,一个连续的进位段一定某个\(A\)段的末尾的\((1,1)\)开始,到前面的\(B\)段的末尾的\((0,0)\)结束,同时:
- 其它所有\(A\)位都有\((1,1),(1,0),(0,1)\)三种选法
- 其它所有\(B\)位都有\((0,0),(1,0),(0,1)\)三种选法
因此我们可以把\((0,0),\cdots,(1,1)\)这样的状态归为一段,考虑枚举它的段数\(i\)
这样划分的方案数就是把\(k\)分成\(i\)份,每份不能为空的方案数,运用隔板法发现这就是\(C_{k-1}^{i-1}\)
接下来考虑在这些进位段之间一定有一些不进位段(对应上面的其它\(B\)位),但是要注意不进位段的段数可能是\(i-1\)或\(i\)或\(i+1\)
这里直接引用下每日一棵splay大佬sol里的图,就是要注意开头结尾的情况分类
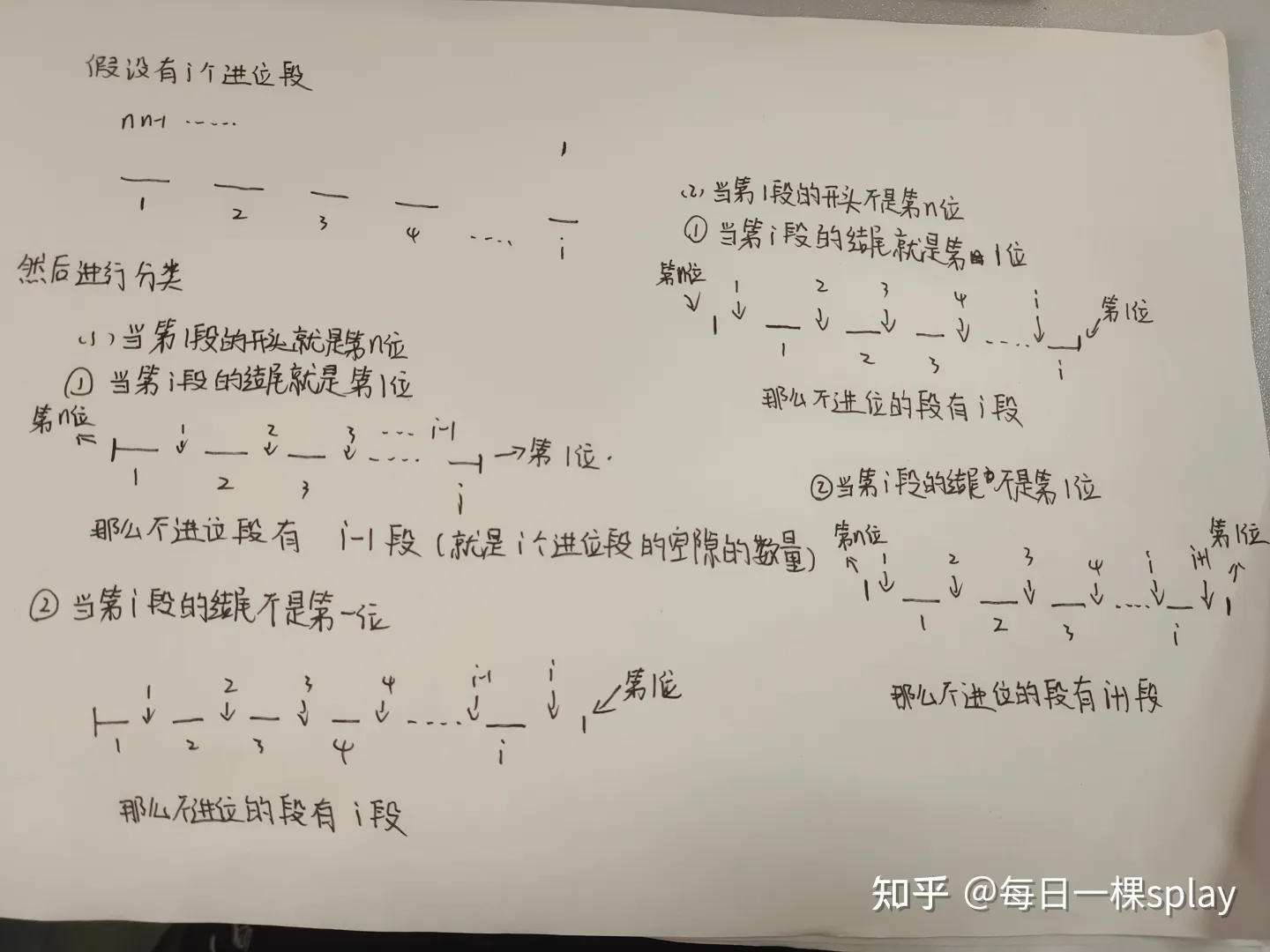
那么代码就很好写了
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=1000005,mod=1e9+7;
int n,k,fac[N],ifac[N],pw[N],ans;
inline void inc(int& x,CI y)
{
if ((x+=y)>=mod) x-=mod;
}
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline int C(CI n,CI m)
{
if (n<0||m<0||m>n) return 0;
return 1LL*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
inline void init(CI n)
{
RI i; for (fac[0]=i=1;i<=n;++i) fac[i]=1LL*fac[i-1]*i%mod;
for (ifac[n]=quick_pow(fac[n]),i=n-1;~i;--i) ifac[i]=1LL*ifac[i+1]*(i+1)%mod;
for (pw[0]=i=1;i<=n;++i) pw[i]=3LL*pw[i-1]%mod;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
if (scanf("%d%d",&n,&k),!k) return printf("%d",quick_pow(3,n)),0;
RI i; for (init(n),i=1;i<=k;++i)
{
if (i*2<=n) inc(ans,1LL*C(k-1,i-1)*C(n-k,i)%mod*pw[n-i*2]%mod);
if (i*2-1<=n) inc(ans,1LL*C(k-1,i-1)*C(n-k,i-1)%mod*pw[n-i*2+1]%mod);
}
return printf("%d",ans),0;
}
E. Make It Connected
改了好久一点点加结论,WA了好几发可算是过了
其实就是个找性质题,我们容易发现首先分出所有的联通块
然后一种obvious的想法,若这个联通块不是一个团(即这个子图是个完全图),那么我们直接操作里面度数最小的一个节点即可
不难发现这样这个点可以和其它的联通块联通,并且它还可以保证和这个联通块联通,同时这个联通块剩下的部分也联通
嘛听起来看似很莫名其妙,其实画几个图就一看便知,那么接下来考虑所有联通块都是团的情况
刚开始是naive跟着样例想了下以为就是一直操作点数最小的那个团,但交上去发现WA了
但是由于是赛后补题,所以我们可以面向数据编程,虽然不能把数据下载下来,但是看到我输出的几百个点,答案只有两个点顿时想到了什么
如果只有两个联通块时,那么只能一直操作点数较少的那个
但如果有三个及以上个联通块时,那么我们随便挑两个不同的联通块里的点操作即可
最后再注意一下一开始所有点都联通的情况和一个孤立的点的情况
#include<cstdio>
#include<vector>
#define RI register int
#define CI const int&
using namespace std;
const int N=4005;
int t,n,pnt,edg,stk[N],deg[N],cnt,cut;
char s[N][N]; bool vis[N],g[N][N]; vector <int> v[N],ans[N];
inline void DFS(CI now)
{
vis[now]=1; stk[++pnt]=now; for (int to:v[now])
{
if (!g[now][to]) ++edg,++deg[now],++deg[to],g[now][to]=g[to][now]=1;
if (!vis[to]) DFS(to);
}
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i,j; for (scanf("%d",&n),i=1;i<=n;++i) for (vis[i]=deg[i]=0,v[i].clear(),j=1;j<=n;++j) g[i][j]=0;
for (i=1;i<=n;++i) for (scanf("%s",s[i]+1),j=1;j<=n;++j) if (s[i][j]=='1') v[i].push_back(j);
bool flag=0,sign=0; int mi=1e9; for (i=1;i<=cnt;++i) ans[i].clear(); cnt=0;
for (i=1;i<=n&&!flag&&!sign;++i) if (!vis[i])
{
pnt=edg=0; DFS(i); if (pnt==n) sign=1;
if (!edg) flag=1,cut=i; else
if (edg!=pnt*(pnt-1)/2)
{
int pos=-1; for (flag=1,j=1;j<=pnt;++j)
if (!~pos||deg[stk[j]]<deg[pos]) pos=stk[j]; cut=pos;
} else
{
for (++cnt,j=1;j<=pnt;++j) ans[cnt].push_back(stk[j]);
}
}
if (sign) { puts("0"); continue; }
if (flag) { printf("1\n%d\n",cut); continue; }
if (cnt==2)
{
printf("%d\n",min(ans[1].size(),ans[2].size()));
for (int x:ans[ans[1].size()<ans[2].size()?1:2])
printf("%d ",x); putchar('\n');
} else printf("2\n%d %d\n",ans[1][0],ans[2][0]);
}
}
Postscript
妈的后面的题都是3000+直接跑路,应该是很难的DP题
由于最近微积分和线代的作业贼多,因此欠下来的比赛场次也比较多,需要狠狠地补一下


 浙公网安备 33010602011771号
浙公网安备 33010602011771号