AtCoder Regular Contest 150
Preface
我现在怎么这么菜啊呜呜呜……
一个B挂了好久,CWA了一整页也没过(脑抽),脑子抽风了属于是
A - Continuous 1
妈的刚开始题目看错了太艹了,直接枚举每个长度为\(k\)的区间,需要满足区间外没有\(1\)并且区间内没有\(0\),这样的区间有且只能有一个
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=300005;
int t,n,k,pfx1[N],pfx0[N],c; char s[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d%d%s",&n,&k,s+1),i=1;i<=n;++i)
pfx0[i]=pfx0[i-1]+(s[i]=='0'),pfx1[i]=pfx1[i-1]+(s[i]=='1');
for (c=0,i=1;i<=n-k+1;++i)
if (pfx1[i-1]==0&&pfx1[n]-pfx1[i+k-1]==0&&pfx0[i+k-1]-pfx0[i-1]==0) ++c;
puts(c==1?"Yes":"No");
}
return 0;
}
B - Make Divisible
刚开始不知道为什么就觉得\(x\)能取的范围一定很小,就枚举了个\(10^6\)上去,白WA了两发
首先我们可以把\(A+x|B+y\)等价变为\(B+n=(A+m)\times k\),其中\(n<A+m\),最后的贡献就是\(n+m\)
现在我们考虑通过调整\(m\)的值,让\(n\)的值改变,不难发现当\(m\)变大时,若\(k\)的值不变化,那么\(n\)显然是增大的,这些情况一定不是最优的
因此我们每次变化\(m\)的时候都要求\(k\)变化,直到\(n=0\)为止,单组数据复杂度大概是\(O(\log n)\)级别的
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
int t,a,b,ans;
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
scanf("%d%d",&a,&b); int m=(b-1)/a+1,n=m*a-b,pa=a; ans=n;
while (n>0&&a<=b)
{
int d=(a-n-1)/m; a+=d; m=(b-1)/a+1; n=m*a-b; ans=min(ans,n+a-pa);
++a; m=(b-1)/a+1; n=m*a-b; ans=min(ans,n+a-pa);
}
printf("%d\n",ans);
}
return 0;
}
C - Path and Subsequence
刚开始脑抽了以为DFS能过的,后来发现是找最短路径就写了个分层图,愣是没想到01-BFS
不难发现我们可以设\(f_i\)表示到点\(i\)匹配到\(B\)序列的第几项了,考虑从\(i\)走到它的邻点\(j\),则\(f_j=\min_\limits{i\to j}(f_i+[a_j=b_{f_i+1}])\)
此时问题变为一个最短路问题,不难发现由于边权只能是\(0/1\),因此可以用01-BFS解决
#include<cstdio>
#include<iostream>
#include<vector>
#include<deque>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int n,m,k,x,y,a[N],b[N],f[N]; vector <int> v[N]; deque <int> q; bool vis[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d%d%d",&n,&m,&k),i=1;i<=m;++i)
scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
for (i=1;i<=n;++i) scanf("%d",&a[i]),f[i]=k+1;
for (i=1;i<=k;++i) scanf("%d",&b[i]);
f[1]=a[1]==b[1]; vis[1]=1; q.push_back(1);
while (!q.empty())
{
int now=q.front(); q.pop_front(); vis[now]=0;
for (int to:v[now])
{
int d=a[to]==b[f[now]+1];
if (f[now]+d<f[to])
{
vis[to]=1; f[to]=f[now]+d;
if (d) q.push_back(to); else q.push_front(to);
}
}
}
return puts(f[n]<k?"No":"Yes"),0;
}
D - Removing Gacha(NTT做法)
首先设\(X_k\)表示从第一次出现\(k\)个黑色点到第一次出现\(k+1\)个黑色点的期望步数,最终的答案就是\(\sum_{k=0}^{N-1} X_k\)
考虑当有\(k\)个黑色点时,good的点的个数为\(m\),显然此时选中一个白色点让状态转移到\(k+1\)的概率是\(\frac{N-k}{N-m}\),期望步数就是\(\frac{N-m}{N-k}\)
设\(p_{k,m}\)表示当有\(k\)个黑色点,good的点的个数为\(m\)这种局面出现的概率,那么有\(E_k=\sum_{m=0}^N \frac{p_{k,m}\times(N-m)}{N-k}=\frac{N}{N-k}-\frac{1}{N-k}\times \sum_{m=0}^N (p_{k,m}\times m)\)
不难发现,\(\sum_{m=0}^N (p_{k,m}\times m)\)就是当第一次出现\(k\)个黑色点时,good点数的期望
考虑设\(q_{k,i}\)表示点\(i\)在第一次出现\(k\)个黑色点时,它是good的概率,因此\(\sum_{m=0}^N (p_{k,m}\times m)=\sum_{i=1}^N q_{k,i}\)
设\(dep_i\)表示从根节点到\(i\)点的节点个数,显然此时问题变为,在\(N\)个点中选出\(k\)个点变黑,并且这\(k\)个点中恰好包含了\(dep_i\)个给定的点,不难发现这部分的概率是\(\frac{C_{N-dep_i}^{k-dep_i}}{C_N^k}=\frac{k!(N-dep_i)!}{N!(k-dep_i)!}\)
因此现在问题转化为求\(\frac{k!}{N!}\times \sum_\limits{1\le i\le N,dep_i\le k} \frac{(N-dep_i)!}{(k-dep_i)!}\),考虑记\(c_i\)为\(dep_v=i\)的\(v\)的个数,则\(\sum_\limits{1\le i\le N,dep_i\le k} \frac{(N-dep_i)!}{(k-dep_i)!}=\sum_{i=1}^k c_i\times \frac{(N-i)!}{(k-i)!}\)
考虑设\(A_i=c_i\times (N-i)!,B_i=\frac{1}{i!}\),显然我们要求的东西就是\(A\star B\),直接NTT求解即可
复杂度\(O(N\log N)\)
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005,mod=998244353;
int n,dep[N],c[N],fa,lim,fac[N],ifac[N],A[N<<2],B[N<<2],ans;
inline int sum(CI x,CI y)
{
return x+y>=mod?x+y-mod:x+y;
}
inline int sub(CI x,CI y)
{
return x-y<0?x-y+mod:x-y;
}
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline void init(CI n)
{
RI i; for (fac[0]=i=1;i<=n;++i) fac[i]=1LL*fac[i-1]*i%mod;
for (ifac[n]=quick_pow(fac[n]),i=n-1;~i;--i) ifac[i]=1LL*ifac[i+1]*(i+1)%mod;
}
namespace Poly
{
int p,rev[N<<2];
inline void init(CI n)
{
for (lim=1,p=0;lim<=n;lim<<=1,++p);
for (RI i=0;i<lim;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<p-1);
}
inline void NTT(int *f,CI opt)
{
RI i,j,k; for (i=0;i<lim;++i) if (i<rev[i]) swap(f[i],f[rev[i]]);
for (i=1;i<lim;i<<=1)
{
int D=quick_pow(3,~opt?(mod-1)/(i<<1):mod-1-(mod-1)/(i<<1));
for (j=0;j<lim;j+=(i<<1))
{
int W=1; for (k=0;k<i;++k,W=1LL*W*D%mod)
{
int x=f[j+k],y=1LL*f[i+j+k]*W%mod; f[j+k]=sum(x,y); f[i+j+k]=sub(x,y);
}
}
}
if (!~opt)
{
int Div=quick_pow(lim); for (i=0;i<lim;++i) f[i]=1LL*f[i]*Div%mod;
}
}
};
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),dep[1]=1,i=2;i<=n;++i) scanf("%d",&fa),dep[i]=dep[fa]+1;
for (init(n),i=1;i<=n;++i) ++c[dep[i]];
for (i=0;i<=n;++i) A[i]=1LL*c[i]*fac[n-i]%mod,B[i]=ifac[i];
for (Poly::init(n<<1),Poly::NTT(A,1),Poly::NTT(B,1),i=0;i<lim;++i) A[i]=1LL*A[i]*B[i]%mod;
for (Poly::NTT(A,-1),i=0;i<n;++i) ans=sum(ans,1LL*sub(n,1LL*A[i]*fac[i]%mod*ifac[n]%mod)*quick_pow(n-i)%mod);
return printf("%d",ans),0;
}
D - Removing Gacha(简便做法)
我们考虑直接求点\(i\)期望被染色的次数\(x_i\),答案就是\(\sum_{i=1}^N x_i\)
考虑单独看一个点\(i\),显然只要考虑从根节点到点\(i\)的这条链的操作即可,并且一直操作直到这条链上的所有点都变成黑色
发现问题的难点在于每次只能选一个非good的点进行操作,而根据前面的做法我们知道考虑上这种情况是非常麻烦的
那么我们现在不妨假设对于这条链上的所有点(包括good点)也可以进行操作,只不过我们忽略这些操作
具体来说,因为我们最后只关心最后\(i\)变成good的时候期望选择了它多少次,只统计\(x_i\),我们完全可以假设对于链上的good的点也进行了操作,无论其他的点怎么操作都不会影响这条链的状态和\(i\)的答案
那么现在问题就很简单了,一条链上有\(k\)个点,初始时全为白色,每次选择其中任意一个点染成黑色,问把所有点都变黑时其中一个点被染色的期望次数时多少
考虑直接求出总操作次数的期望,当此时有\(i\)个白色点时,下一次选到白色点的概率是\(\frac{i}{k}\),期望步数就是\(\frac{k}{i}\),那么下次就有\(i-1\)个个白色点,以此类推,这部分的期望就是\(\sum_{i=1}^k \frac{k}{i}\)
因此每个点的期望就是\(\sum_{i=1}^k\frac{1}{i}\),代码非常简洁,复杂度\(O(n)\)
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005,mod=998244353;
int n,dep[N],fa,lim,fac[N],ifac[N],g[N],ans;
inline int sum(CI x,CI y)
{
return x+y>=mod?x+y-mod:x+y;
}
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline void init(CI n)
{
RI i; for (fac[0]=i=1;i<=n;++i) fac[i]=1LL*fac[i-1]*i%mod;
for (ifac[n]=quick_pow(fac[n]),i=n-1;~i;--i) ifac[i]=1LL*ifac[i+1]*(i+1)%mod;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),dep[1]=1,i=2;i<=n;++i)
scanf("%d",&fa),dep[i]=dep[fa]+1;
for (init(n),i=1;i<=n;++i) g[i]=sum(g[i-1],1LL*ifac[i]*fac[i-1]%mod);
for (i=1;i<=n;++i) ans=sum(ans,g[dep[i]]);
return printf("%d",ans),0;
}
E - Weathercock
首先,我们考虑把问题转化成R比L多的情况,若L比R多那么我们可以翻转数列然后把L和R反转变成前面的情况
相等的情况可以特殊考虑,若L和R的数量相等时所有人最多只会转向一次,直接算即可
首先先仅考虑\(t=0.5\)的情况,我们考虑把L看作\(-1\)把R看作\(1\),并统计出关于这的前缀和\(f_i\),考虑我们可以这样判断一个人是否要转向:
- 若\(s_i=L\),若\(f_i\ge 0\),则\(i\)转向
- 若\(s_i=R\),若\(f_i>f_{NK-1}\),则\(i\)转向
由上面我们可以归结出,若\(\min(f_i,f_{i-1})\ge f_{NK-1}\),那么不论\(s_i\)为何值他一定会转向
借用官方题解的一个分析,若\(N=15,K=1,S=RRRLRLLLLRRRLLR\),以\(i\)为横坐标,\(f_i\)为纵坐标作图然后把点都连起来
考虑其中红色的线段表示满足\(\min(f_i,f_{i-1})\ge f_{NK-1}\)且\(s_i=R\)的人,蓝色的线段表示满足\(\min(f_i,f_{i-1})\ge f_{NK-1}\)且\(s_i=L\)的人

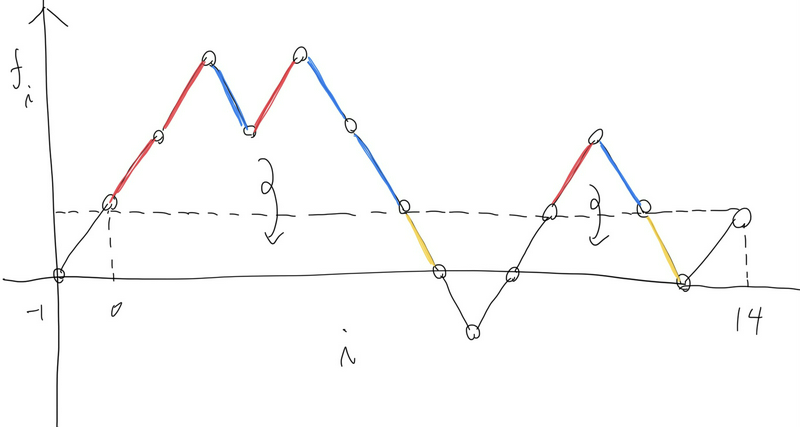
不难发现我们可以把所有在\(f_{NK-1}\)以上的部分全部折叠下来,因此在\(t=0.5\)的操作过后\(f_{NK-1}\)就变成了最大的那个数
这样之后那些被折下去的L在变成R之后就再也不能翻上来了,因此它们对答案的贡献只有\(1\)
现在考虑黄色的线段部分,它们是那些满足\(s_i=L\)的人但\(f_i<f_{NK-1}\)的人,我们现在考虑它们在什么时候才会变成R
首先我们先把目光放在\(t=1.5\)时,不难发现此时所有的\(s_i=R\)的位置已经不会再变化了,因此\(f_{NK-1}\)也将一直维持最大值不变,这又会导致\(s_i=R\)的人在接下来的时间也不会转向
因此我们只要考虑还等于L的人,我们设\(k\)为第一个使得\(f_k>0\)的数,由于对于\(i<k\)的所有人均有\(f_i\le 0\),因此这些\(s_i\)都不会变化
接下来有一个重要的结论,若在\(k\)的右侧有\(x\)个人为\(s_i=L\),那么在下一次变换后它的右侧最多还有\(x-1\)给人为\(s_i=L\)
证明的话也很简单,让\(m\)为\(k\)右侧第一个\(s_i=L\)的人,则\(f_m=f_{m-1}-1\),我们可以得出\(f_{m-1}\ge f_k=1\),因此不难发现\(f_m\ge 0\)
根据前面的结论,\(m\)将会在下一次变换时转向,而所有\(s_i=R\)的人不会转向,因此最多还剩\(x-1\)个\(s_i=L\)的人
因此不难发现最多只要\(t=O(NK)\)的时间\(k\)右侧的所有人都会变成\(s_i=R\),因此我们可以得出以下总结:
- 满足\(i\ge k\)且\(f_i>f_{NK-1}\)且初始时\(s_i=R\)的人会变向两次:\(R\to L\to R\)
- 满足\(i\ge k\)且初始时\(s_i=R\)的人总会变向一次:\(L\to R\)
- 满足\(i<k\)的所有人永远不会改变方向
因此我们现在可以直接算答案了,由于\(f_i=\lfloor\frac{i}{N}\rfloor\cdot f_{N-1}+f_{i\ \bmod \ N}\),因此把所有模\(N\)同余的位置一起考虑即可,具体实现看代码
(啊好久没写过这么长的题解了真是舒爽)
#include<cstdio>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005,mod=998244353;
int n,k,pfx[N]; long long sum,ans; char s[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d%d%s",&n,&k,s+1),i=1;i<=n;++i) pfx[i]=pfx[i-1]+(s[i]=='R'?1:-1);
if (pfx[n]<0)
{
for (reverse(s+1,s+n+1),i=1;i<=n;++i) s[i]=s[i]=='R'?'L':'R';
for (i=1;i<=n;++i) pfx[i]=pfx[i-1]+(s[i]=='R'?1:-1);
}
if (!pfx[n])
{
for (i=1;i<=n;++i) if (s[i]=='L'&&pfx[i]>=0) ans+=k;
else if (s[i]=='R'&&pfx[i]>pfx[n]) ans+=k;
return printf("%d",ans%mod),0;
}
int pos=1; while (pfx[pos]<=0) ++pos;
for (i=1;i<=n;++i) if (s[i]=='L') ans+=k; else
ans+=2LL*max(0LL,(k-max(0LL,(1LL*pfx[n]*k-pfx[i])/pfx[n]+1)));
for (i=1;i<=pos;++i) if (s[i]=='L') --ans;
else if (1LL*pfx[n]*k<pfx[i]) --ans;
return printf("%d",ans%mod),0;
}
Postscript
刚解决完欠的两场ARC周日又有新的ARC了,话说好像要去上晚自习没法在线打了有点遗憾的说

