Codeforces Round #819 (Div. 1 + Div. 2) and Grimoire of Code Annual Contest 2022
Preface
明天的CF一定打啊(绝对不咕),今天白天补现代作业,英语作业到哭,而且还要准备四六级,每天逼着自己背单词
A. Mainak and Array
不难发现换中间的数不会影响答案,因此操作的区间只可能是\([1,k],[k,n](k\in [1,n])\),讨论一下即可
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=2005;
int t,n,a[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d",&n),i=1;i<=n;++i) scanf("%d",&a[i]);
int ans=-2000; for (a[n+1]=a[1],i=1;i<=n;++i) ans=max(ans,a[i]-a[i+1]);
int cur=0; for (i=2;i<=n;++i) cur=max(cur,a[i]); ans=max(ans,cur-a[1]);
for (cur=1000,i=1;i<n;++i) cur=min(cur,a[i]); ans=max(ans,a[n]-cur);
printf("%d\n",ans);
}
return 0;
}
B. Mainak and Interesting Sequence
考虑以下构造法,设\(p=\lfloor\frac{m}{n}\rfloor,q=m\bmod n\),开始时先把所有数赋值成\(p\),然后分类讨论:
- \(n\)为奇数,则此时我们可以任选一个\(a_i\)将其加上\(q\)以满足题意
- \(n\)为偶数且\(q\)为偶数,则此时我们可以任选两个\(a_i\),将其各加上\(\frac{q}{2}\)以满足题意
- \(n\)为偶数且\(q\)为奇数,不难发现此时无解
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int t,n,m,a[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; scanf("%d%d",&n,&m); int p=m/n,q=m%n;
if (n>m||((n&1)==0&&(q&1))) { puts("No"); continue; }
for (puts("Yes"),i=1;i<=n;++i) a[i]=p;
if (n&1) a[n]+=q; else a[n-1]+=q/2,a[n]+=q/2;
for (i=1;i<=n;++i) printf("%d%c",a[i]," \n"[i==n]);
}
return 0;
}
C. Jatayu's Balanced Bracket Sequence
看到括号序列先来个前缀和,把(看作1,)看作-1,设其前缀和为\(pfx_i\)
考虑一个区间\([l,r]\)时合法的括号序列当且仅当:
- \(a_l\)是左括号,\(a_r\)是右括号
- \(pfx_{l-1}=pfx_r\)且\([l,r]\)中没有比\(pfx_r\)小的元素
考虑到后面一个条件较难满足,我们考虑每次对于一个右括号\(a_i\)找出距它最近的且\(pfx_{j-1}=pfx_i\)的左括号\(a_j\)
不难发现此时\(pfx_k,k\in[j,i]\)中一定没有小于\(pfx_j\)的元素,否则\(j\)就不是最近的了
但是配对的时候不能仅仅把\(i,j\)配对了,我们还要考虑检查\(a_{j-1}\)是不是一个合法的右括号
若是,因为\(pfx_{j-1}=pfx_i\),因此\(a_{j-1}\)可配对的括号\(a_i\)也一定可以配对,因此直接把\(i,j-1\)配对即可
用并查集维护连通块信息即可
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005;
int t,n,a[N],fa[N],cur,pre[N],ans; bool vis[N];
inline int getfa(CI x)
{
return x!=fa[x]?fa[x]=getfa(fa[x]):x;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; char ch;for (scanf("%d",&n),n<<=1,i=0;i<=n;++i) fa[i]=i,pre[i]=-1,vis[i]=0;
for (cur=0,i=1;i<=n;++i)
{
while (ch=getchar(),ch!='('&&ch!=')'); a[i]=ch=='('?1:-1;
if (a[i]==1) pre[cur]=i,cur+=a[i]; else
{
cur+=a[i]; if (~pre[cur])
{
vis[i]=1; fa[getfa(i)]=getfa(pre[cur]);
if (pre[cur]&&vis[pre[cur]-1]) fa[getfa(i)]=getfa(pre[cur]-1);
}
}
}
for (ans=0,i=1;i<=n;++i) ans+=getfa(i)==i; printf("%d\n",ans);
}
return 0;
}
D. Edge Split
又是构造题,构造题精通被动触发
首先不难发现必然有一种颜色的边要形成一棵生成树,证明如下
设红色边集合为\(R\),连通块数量为\(c_1\),蓝色边集合为\(B\),连通块数量为\(c_2\),假设\(R\)不是生成树
则我们必然可以找到一条\(B\)中的边,使得在\(R\)中这条边连接了两个连通块
考虑到如果把这条边从\(B\)拿到\(R\),显然\(c_1\)是一定减\(1\)的,但是\(c_2\)至多加\(1\),因此一定不会变劣
同样的,若\(R\)中存在环,则我们对于环上的任意一条边,把它从\(R\)拿到\(B\)上,显然\(c_1\)不会变,而\(c_2\)可能会减\(1\),亦不会变劣
综上,当\(R\)为生成树时答案一定时最优的,因此我们考虑先随机的生成一个生成树\(R\),然后查看剩下的最多三条边
不难发现,只要剩下的边没有成环那么对答案的影响都是一样的,而由于两条及以下的边不可能成环,因此只要考虑三条边的情况
显然,这个环上的三个点在\(R\)的生成树上一定是在某条链上,我们直接断掉最下方的点的树边然后把其中一条返祖边变成树边即可
如图,黑色边是树边,绿色和蓝色边是返祖边,它们形成了一个环,我们可以断开红色的树边,并将任一条蓝色的边变成树边即可
单组数据复杂度\(O(n)\)
#include<cstdio>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005;
struct edge
{
int to,nxt;
}e[N<<1]; int t,n,m,u[N],v[N],cnt,head[N],dep[N],deg[N],tot,num[N],anc[N]; bool vis[N],cs[N];
inline void addedge(CI x,CI y)
{
e[++cnt]=(edge){y,head[x]}; head[x]=cnt;
e[++cnt]=(edge){x,head[y]}; head[y]=cnt;
}
inline bool cmp(CI x,CI y)
{
return dep[x]<dep[y];
}
#define to e[i].to
inline void DFS(CI now=1,CI fa=0)
{
vis[now]=1; dep[now]=dep[fa]+1; anc[now]=fa;
for (RI i=head[now];i;i=e[i].nxt) if (!vis[to]) cs[i>>1]=1,DFS(to,now);
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d%d",&n,&m),i=cnt=1;i<=n;++i) head[i]=vis[i]=deg[i]=0;
for (i=1;i<=m;++i) scanf("%d%d",&u[i],&v[i]),addedge(u[i],v[i]),cs[i]=0;
for (DFS(),i=1;i<=m;++i) if (!cs[i]) ++deg[u[i]],++deg[v[i]];
for (tot=0,i=1;i<=n;++i) if (deg[i]) num[++tot]=i;
bool flag=tot==3; for (i=1;i<=tot&&flag;++i) if (deg[num[i]]!=2) flag=0;
if (flag)
{
sort(num+1,num+4,cmp); int add,del; for (i=head[num[3]];i;i=e[i].nxt)
{
if (!cs[i>>1]&&to==num[1]) add=i>>1;
if (cs[i>>1]&&to==anc[num[3]]) del=i>>1;
}
cs[add]=1; cs[del]=0;
}
for (i=1;i<=m;++i) putchar(cs[i]+'0'); putchar('\n');
}
return 0;
}
E. Almost Perfect
没有置换环的思维意识所以完全没思路的说
考虑构建一张\(n\)个点的图,其中\(i\)与\(p_i,p_i^{-1}\)连边,如下图
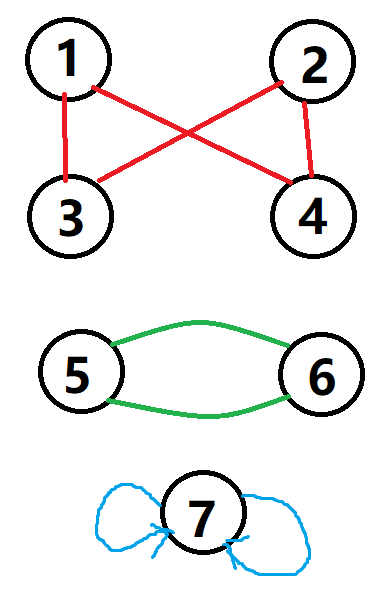
共有三种环满足条件:
- 四元环,节点编号分别为\(i,i+1,j,j+1\),且连接方式如图
- 二元环,两点\(i,j\)之间存在重边
- 一元环,即点\(i\)形成的自环
考虑到四元环的特殊性,我们枚举四元环的个数\(m\),问题转化为从\([1,n)\)中选出\(2m\)个两两不相邻的数
设这些数为\(a_1,a_2,\cdots,a_{2m}\),则要求:
选择的方案数为\(C_{n-2m}^{2m}\),然后考虑配对的问题,由于这里\((i,j)\)和\((j,i)\)不等价,因此方案数是\(\frac{(2m)!}{m!}\)
接下来只要考虑算出\(f_n\)表示\(n\)个点全部形成一元环和二元环的方案数即可,显然转移有\(f_i=f_{i-1}+(i-1)\times f_{i-2}\)
预处理一下\(f\)即可\(O(n)\)处理询问,据说还有用卷积优化的方法,但是这里没有必要就不写了(才不是把NTT忘光了呢)
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=300005,mod=998244353;
int t,n,fac[N],ifac[N],f[N],ans;
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline void init(CI n)
{
RI i; for (fac[0]=i=1;i<=n;++i) fac[i]=1LL*fac[i-1]*i%mod;
for (ifac[n]=quick_pow(fac[n]),i=n-1;~i;--i) ifac[i]=1LL*ifac[i+1]*(i+1)%mod;
for (f[0]=f[1]=1,i=2;i<=n;++i) f[i]=(1LL*(i-1)*f[i-2]%mod+f[i-1])%mod;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (init(300000),scanf("%d",&t);t;--t)
{
scanf("%d",&n); ans=0; for (RI i=0;4*i<=n;++i)
(ans+=1LL*fac[n-2*i]*ifac[n-4*i]%mod*ifac[i]%mod*f[n-4*i]%mod)%=mod;
printf("%d\n",ans);
}
return 0;
}
Postscript
感觉后面的题目难度有点高,而且F还被ban了,先跑路了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号