COMPFEST 14 - Preliminary Online Mirror
Preface
9/10:今天不知道为什么一整天头疼的一批,而且牙也疼的吃不了饭,实在写不动题目啊
9/11:晚上发烧了,结果睡了一晚竟然好了……我的自愈能力原来这么强的嘛awa
9/12:得知错过了校队的第一轮选拔(没收到通知qaq),得等大一下才有机会了
9/13,9/14:最近网课排满了课务压力好大的说,一天八节课加早自习没时间写题了捏,而且还要完成学习程序设计课的作业,头疼ing
9/15:一天只能写一题了QAQ
9/16,9/17:后面的题挺难的,加油冲完它
不过自己写写题也比较轻松没什么压力,但接下来得准点打比赛了不能天天VP
下面题目做的顺序排,大致是按难度递增的把
A. Accumulation of Dominoes
SB题,注意特判\(m=1\)的情形
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
int n,m;
int main()
{
scanf("%d%d",&n,&m); if (m==1) return printf("%d",n-1),0;
return printf("%lld",1LL*n*(m-1)),0;
}
B. Basketball Together
SB题,贪心地从大到小考虑每个人为队长,拉队员的话就从小的开始拉
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int n,d,a[N],ans;
int main()
{
RI i,j; for (scanf("%d%d",&n,&d),i=1;i<=n;++i) scanf("%d",&a[i]);
for (++d,sort(a+1,a+n+1),i=0,j=n;i<j;--j)
{
int k=(d-1)/a[j]; if (i+k<j) i+=k,++ans; else break;
}
return printf("%d",ans),0;
}
G. Garage
貌似之前有过哪个题目有这个结论的说
直接说结论,\(x\)是合法的当且仅当\(x\)是大于等于\(3\)的奇数或大于等于\(8\)的\(4\)的倍数
证明,若\(x=2k+1,k\ge 1\),显然当\(b=k+1,a=k\)时符合,若\(x=4k+4,k\ge 1\),显然当\(b=k+2,a=k\)时符合
那么剩下来不符合的就是形如\(4k+2,k\ge 1\)的数了,不难发现由于\(a^2.b^2\)对\(4\)取模后的结果要么是\(0\)要么是\(1\),因此\(b^2-a^2\)对\(4\)取模的结果必不可能是\(2\)
计算答案的话可以直接二分,求\(\le x\)中有多少个合法的数即可
#include<cstdio>
#include<iostream>
#define int long long
#define RI register int
#define CI const int&
using namespace std;
int n,ans;
inline int count(CI x)
{
return (x+1)/2-1+(x>=4?x/4-1:0);
}
signed main()
{
scanf("%lld",&n); int l=3,r=2147483647,mid;
while (l<=r)
{
mid=l+r>>1; if (count(mid)>=n) ans=mid,r=mid-1; else l=mid+1;
}
return printf("%lld",ans),0;
}
M. Moving Both Hands
一个朴素的想法,设\(d(x,y)\)表示\(x\)到\(y\)的最短路,考虑枚举中间点,对于\((1,v)\)的答案就是\(\min_\limits{1\le i\le n} d(1,i)+d(v,i)\)
将原图中的边反向,设\(d'(x,y)\)表示反向图中\(x\)到\(y\)的最短路,此时答案为\(\min_\limits{1\le i\le n} d(1,i)+d'(i,v)\)
考虑对每个点增加一个状态,设\((x,0/1)\)表示到\(x\)的最短路,第二维表示是否反向,此时有:
- 对于每条边\((u,v,w)\),连\((u,0)\to (v,0)\)权值为\(w\)的边,以及\((v,1)\to (u,1)\)权值为\(w\)的边
- 对于每个点\(v\),连\((v,0)\to (v,1)\),权值为\(0\)的边
这样直接跑一遍Dijkstra即可,最后点\(v\)的答案就是\((1,0)\)到\((v,1)\)的最短路
#include<cstdio>
#include<queue>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005;
const long long INF=1e18;
struct edge
{
int to,nxt,v;
}e[N<<2]; int n,m,head[N],cnt,x,y,z; long long dis[N]; bool vis[N];
struct data
{
long long v; int p;
inline data(const long long& V=0,CI P=0) { v=V; p=P; }
friend inline bool operator < (const data& A,const data& B)
{
return A.v>B.v;
}
}; priority_queue <data> hp;
inline void addedge(CI x,CI y,CI z)
{
e[++cnt]=(edge){y,head[x],z}; head[x]=cnt;
}
#define to e[i].to
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d%d",&n,&m),i=1;i<=m;++i)
scanf("%d%d%d",&x,&y,&z),addedge(x,y,z),addedge(n+y,n+x,z);
for (i=1;i<=n;++i) addedge(i,n+i,0);
for (i=1;i<=(n<<1);++i) dis[i]=INF; dis[1]=0;
hp.push(data(dis[1],1)); while (!hp.empty())
{
int now=hp.top().p; hp.pop(); if (vis[now]) continue; vis[now]=1;
for (i=head[now];i;i=e[i].nxt) if (dis[to]>dis[now]+e[i].v)
hp.push(data(dis[to]=dis[now]+e[i].v,to));
}
for (i=2;i<=n;++i) printf("%lld ",dis[n+i]!=INF?dis[n+i]:-1);
return 0;
}
C. Circular Mirror
首先不难发现存在直角三角形的充要条件是:存在某个颜色,其颜色点数大于等于\(3\)且其中的两点恰好在一直径上
首先我们可以扫一遍求出一共有多少对点对在一直径上,记为\(cnt\),剩下的自由点记为\(left=n-cnt*2\)
考虑枚举恰好有多少对直径点对的颜色相同,记为\(i\),那么此时的贡献即为:
首先前面的\(C_{cnt}^i\times C_m^i\times i!\)表示从\(cnt\)个点对中选出\(i\)对并且找出\(i\)种颜色一一匹配的方案数,\([(m-i)\times (m-i-1)]^{cnt-i}\)表示剩余的\(cnt-i\)个点对的选法(此时两两颜色不同),\((m-i)^{left}\)表示剩下的自由点的选法
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=300005,mod=998244353;
int n,m,a[N],cnt,fac[N],ifac[N],ans; long long pfx[N],sum;
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline void init(CI n)
{
RI i; for (fac[0]=i=1;i<=n;++i) fac[i]=1LL*fac[i-1]*i%mod;
for (ifac[n]=quick_pow(fac[n]),i=n-1;~i;--i) ifac[i]=1LL*ifac[i+1]*(i+1)%mod;
}
inline int C(CI n,CI m)
{
return 1LL*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i,j; for (scanf("%d%d",&n,&m),i=1;i<=n;++i)
scanf("%d",&a[i]),pfx[i]=pfx[i-1]+a[i]; sum=pfx[n];
if (sum%2==0)
{
for (j=0,i=1;i<n;++i)
{
while (pfx[i]-pfx[j]>sum/2LL) ++j;
if (pfx[i]-pfx[j]==sum/2LL) ++cnt;
}
}
for (init(max(m,cnt)),i=0;i<=min(m,cnt);++i)
(ans+=1LL*C(cnt,i)*C(m,i)%mod*fac[i]%mod*quick_pow(1LL*(m-i)*(m-i-1)%mod,cnt-i)%mod*quick_pow(m-i,n-cnt*2)%mod)%=mod;
return printf("%d",ans),0;
}
H. Hot Black Hot White
昨天不小心漏看了这道过的人300+的题了,其实比H,C都简单啊(触发:构造题精通)
首先由于模\(3\)的性质可以转为求一个数每位上数字的和,因此\(\operatorname{concat}(x,y)\equiv(x+y)\mod 3\)
因此\(\operatorname{concat}(A_i, A_j) \times \operatorname{concat}(A_j, A_i) + A_i \times A_j \equiv (A_i+A_j)^2+A_i\times A_j \equiv A_i^2+A_j^2\mod 3\)
稍加讨论,我们发现\(A_i^2\bmod 3\)的值只可能是\(0/1\),一个naive的想法,令\(Z=0/2\),把所有\(A_i^2\bmod 3=0\)的数变白,把所有\(A_i^2\bmod 3=1\)的数变黑,即满足和不会反应的条件
那么这样不一定满足颜色的个数相等,因此我们讨论一下:
- 若\(A_i^2\bmod 3=0\)的数的个数更多,则令\(Z=2\),此时可以给\(A_i^2\bmod 3=0\)的一些数赋予另一种颜色而保持不会发生反应的特性
- 若\(A_i^2\bmod 3=1\)的数的个数更多,则令\(Z=0\),此时可以给\(A_i^2\bmod 3=1\)的一些数赋予另一种颜色而保持不会发生反应的特性
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int n,a[N],b[N],c[2],cnt;
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),i=1;i<=n;++i)
scanf("%d",&a[i]),++c[b[i]=1LL*a[i]*a[i]%3];
if (c[0]>=c[1])
{
for (puts("2"),i=1;i<=n;++i) if (b[i]==1) putchar('1');
else if (b[i]==0&&cnt<n/2) putchar('0'),++cnt; else putchar('1');
} else
{
for (puts("0"),i=1;i<=n;++i) if (b[i]==0) putchar('0');
else if (b[i]==1&&cnt<n/2) putchar('1'),++cnt; else putchar('0');
}
return 0;
}
F. Field Photography
首先由于移动的次数不限,并且最后要满足或起来是一个数,我们考虑令\(k=\operatorname{LSB}(W_j)\),其中\(\operatorname{LSB}(x)\)表示\(x\)的二进制下从低位到高位第一个\(1\)的位置
不难发现由于或的性质,我们每次操作的步数必须是\(2^k\)的倍数,考虑以下一种移动方案:
- 每次对某一行向左或向右移动\(2^k\)的步数
- 最后将某一行先向右移动\(W_j\)的步数,然后再向左移动\(W_j\)的步数
不难发现这样一定是最优的(每次移动的单位长度最短)并且满足题目要求
不难发现此时我们只关心区间端点对\(2^k\)取模后的结果,具体的:
- 若\(r_i-l_i+1\ge 2^k\) ,则\([0,2^k)\)中的每个数都能被覆盖到
- 若\(r_i-l_i+1< 2^k\and l_i\bmod 2^k\le r_i\bmod 2^k\),则\([l_i\bmod 2^k,r_i\bmod 2^k]\)中的每个数都能被覆盖到
- 若\(r_i-l_i+1< 2^k\and l_i\bmod 2^k> r_i\bmod 2^k\),则\([l_i\bmod 2^k,2^k),[0,r_i\bmod 2^k]\)中的每个数都能被覆盖到
因此问题变为区间修改+全局最值,结果我这个傻狗去写线段树,然后常数太大T了,后来一想发现直接差分就好了
由于\(\operatorname{LSB}(x)\)的范围是\(\log W_j\)级别的,总复杂度\(O(n\log n\log W_j)\)
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<utility>
#define RI register int
#define CI const int&
#define mp make_pair
#define fi first
#define se second
using namespace std;
const int N=100005;
typedef pair <int,int> pi;
int n,l[N],r[N],q,x,ans[35],cnt,sum; pi rst[N<<2];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i,j; for (scanf("%d",&n),i=1;i<=n;++i) scanf("%d%d",&l[i],&r[i]);
for (j=0;j<=30;++j)
{
int k=1<<j; for (cnt=0,i=1;i<=n;++i)
if (r[i]-l[i]+1>=k) rst[++cnt]=mp(0,1),rst[++cnt]=mp(k,-1);
else if (l[i]%k<=r[i]%k) rst[++cnt]=mp(l[i]%k,1),rst[++cnt]=mp(r[i]%k+1,-1);
else rst[++cnt]=mp(l[i]%k,1),rst[++cnt]=mp(k,-1),rst[++cnt]=mp(0,1),rst[++cnt]=mp(r[i]%k+1,-1);
for (sort(rst+1,rst+cnt+1),sum=0,i=1;i<=cnt;++i)
sum+=rst[i].se,ans[j]=max(ans[j],sum);
}
for (scanf("%d",&q),i=1;i<=q;++i)
for (scanf("%d",&x),j=0;j<=30;++j)
if ((x>>j)&1) { printf("%d\n",ans[j]); break; }
return 0;
}
L. Lemper Cooking Competition
妙题,首先考虑把\(A_i:=-A_i\)的操作看成\(A_i-=2A_i\),然后考虑对\(A_i\)的前缀和\(pfx_i\)进行操作,设操作位置为\(p\),则
- \(A_p-1+=A_p\),即\(A_p=pfx_p-pfx_{p-1}\),因此\(pfx_{p-1}+=pfx_p-pfx_{p-1}\),则\(pfx_{p-1}=pfx_p\)
- \(A_p-=2A_p\),即\(pfx_{p}-=a_p\),因此\(pfx_p-=pfx_p-pfx_{p-1}\),则\(pfx_p=pfx_{p-1}\)
- 对于其它位置\(i\ne p-1/p\),\(pfx_i\)不变
因此不难发现原来的操作竟然变成了交换两个数,而\(A_i\ge 0\)的条件在\(pfx\)中其实就是要求\(pfx\)单调不降
因此只要求逆序对个数即可,注意特判一些无解的情况
#include<cstdio>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int n,a[N],cnt; long long ans,pfx[N],rst[N];
class Tree_Array
{
private:
long long bit[N];
public:
#define lowbit(x) (x&(-x))
inline void add(int x)
{
for (;x;x-=lowbit(x)) ++bit[x];
}
inline int get(int x,int ret=0)
{
for (;x<=cnt;x+=lowbit(x)) ret+=bit[x]; return ret;
}
#undef lowbit
}T;
inline int find(const long long& x)
{
return lower_bound(rst+1,rst+cnt+1,x)-rst;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),i=1;i<=n;++i) scanf("%d",&a[i]),pfx[i]=pfx[i-1]+a[i];
if (pfx[0]>pfx[n]) return puts("-1"),0;
for (i=1;i<n;++i) if (pfx[i]<pfx[0]||pfx[i]>pfx[n]) return puts("-1"),0;
for (i=1;i<n;++i) rst[++cnt]=pfx[i]; sort(rst+1,rst+cnt+1); cnt=unique(rst+1,rst+cnt+1)-rst-1;
for (i=1;i<n;++i) ans+=T.get(find(pfx[i])+1),T.add(find(pfx[i]));
return printf("%lld",ans),0;
}
K. Kingdom of Criticism
考虑最棘手的3操作,我们发现它是针对全局的,因此我们可以用set来维护所有数值
但这样每次可能要操作的数的个数太多了,因此我们可以用并查集把所有一样的数串在一起
由于每个数最多被合并一次,因此复杂度是对的
此时1操作就变得麻烦,因为我们不能随便的拆解并查集中的数(我记得我很早的时候发明过一个可删除式并查集的来着)
但我们细细一想修改后原来的数留着对其它数也没影响啊,直接新开一个点记录修改后的值即可
复杂度\(O(n\log n\cdot \alpha(n))\)
#include<cstdio>
#include<set>
#include<vector>
#define RI register int
#define CI const int&
#define mp make_pair
#define pb push_back
#define fi first
#define se second
using namespace std;
typedef pair <int,int> pi;
const int N=400005;
set <pi> s; int n,a[N<<1],q,opt,x,y,tot,id[N],fa[N<<1]; vector <int> L,R;
namespace DSU
{
inline int getfa(CI x)
{
return x!=fa[x]?fa[x]=getfa(fa[x]):x;
}
inline void init(CI n)
{
for (RI i=1;i<=n;++i) fa[i]=i;
}
};
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),i=1;i<=n;++i) scanf("%d",&a[i]),id[i]=i,s.insert(mp(a[i],i));
for (scanf("%d",&q),tot=n,DSU::init(n+q),i=1;i<=q;++i)
{
scanf("%d%d",&opt,&x); if (opt!=2) scanf("%d",&y);
switch (opt)
{
case 1:
s.insert(mp(a[id[x]=++tot]=y,tot)); break;
case 2:
printf("%d\n",a[DSU::getfa(id[x])]); break;
case 3:
for (auto it=s.lower_bound(mp(x,0));it!=s.end()&&it->fi<=y;it=s.erase(it))
if (it->fi-x<y-it->fi) L.pb(it->se); else R.pb(it->se);
if (!L.empty())
{
for (auto it:L) fa[it]=L[0]; s.insert(mp(a[L[0]]=x-1,L[0])); L.clear();
}
if (!R.empty())
{
for (auto it:R) fa[it]=R[0]; s.insert(mp(a[R[0]]=y+1,R[0])); R.clear();
}
}
}
return 0;
}
E. Electrical Efficiency
首先考虑单独统计每条边每个质因数的贡献,假设现在把一个质因数\(p\)所有的可行的点集\(S\)求出来了
那么对于某条边\((u,v)\),设断开\((u,v)\)后\(u\)这边的子树内且在\(S\)内的点的个数为\(p\),\(v\)这边的子树内且在\(S\)内的点的个数为\(q\),显然贡献为\(C_p^2\times q+C_q^2\times p\)
在无根树内操作不方便,我们考虑化为有根树,这样只要考虑一个子树内的合法点的数目即可,再用总的个数减一下就是子树外部的个数,就可以很方便的统计一条边的贡献了
我们发现若枚举每个质因数,并把对应点建出虚树,就可以很方便的统计贡献了,这也是题解的做法
但是还有一种更简便的方法,考虑大力对每个数质因数分解,并将子树内的所有质因数的对应点个数信息存到map里
考虑上传答案的时候其实就是合并两个map里的元素,利用启发式合并即可保证复杂度
总复杂度\(O(n\log^2 n)\)
#include<cstdio>
#include<map>
#include<vector>
#define RI register int
#define CI const int
#define fi first
#define se second
using namespace std;
const int N=200005,mod=998244353;
int n,x,y,pri[N],lst[N],cnt,f[N],c[N],ans; vector <int> v[N]; map <int,int> s[N];
inline void inc(int& x,CI y)
{
if ((x+=y)>=mod) x-=mod;
}
inline void dec(int& x,CI y)
{
if ((x-=y)<0) x+=mod;
}
inline void init(CI n)
{
for (RI i=2;i<=n;++i)
{
if (!lst[i]) pri[++cnt]=i,lst[i]=i;
for (RI j=1;j<=cnt&&i*pri[j]<=n;++j)
if (lst[i*pri[j]]=pri[j],i%pri[j]==0) break;
}
}
inline int calc(CI x,int y)
{
y-=x; int z=1LL*x*(x-1)*y/2LL%mod; inc(z,1LL*y*(y-1)*x/2LL%mod); return z;
}
inline void DFS(CI now=1,CI fa=0)
{
for (auto it:s[now]) inc(f[now],calc(it.se,c[it.fi]));
for (int to:v[now]) if (to!=fa)
{
DFS(to,now); if (s[to].size()>s[now].size()) swap(s[to],s[now]),f[now]=f[to];
for (auto it:s[to]) dec(f[now],calc(s[now][it.fi],c[it.fi])),
s[now][it.fi]+=it.se,inc(f[now],calc(s[now][it.fi],c[it.fi]));
}
inc(ans,f[now]);
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),init(200000),i=1;i<=n;++i)
for (scanf("%d",&x);x>1;)
{
y=lst[x]; ++c[y]; s[i][y]=1; while (x%y==0) x/=y;
}
for (i=1;i<n;++i) scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
return DFS(),printf("%d",ans),0;
}
J. Journey
首先考虑simple的没有跳跃操作的情况,考虑每条边的贡献次数,我们发现此时答案的构成如下:
- 对于在树的直径上的边,其对答案的贡献次数为\(1\)
- 对于不在树的直径上的边,其对答案的贡献次数为\(2\)
那么考虑有了跳跃操作后如何,不难发现之前是找一条路径使上面的边贡献次数为\(1\),现在就是找两条
考虑这两条路径的构成形式有两种,第一种是存在一个公共点的,如图(红色和绿色分别代表一条路径)
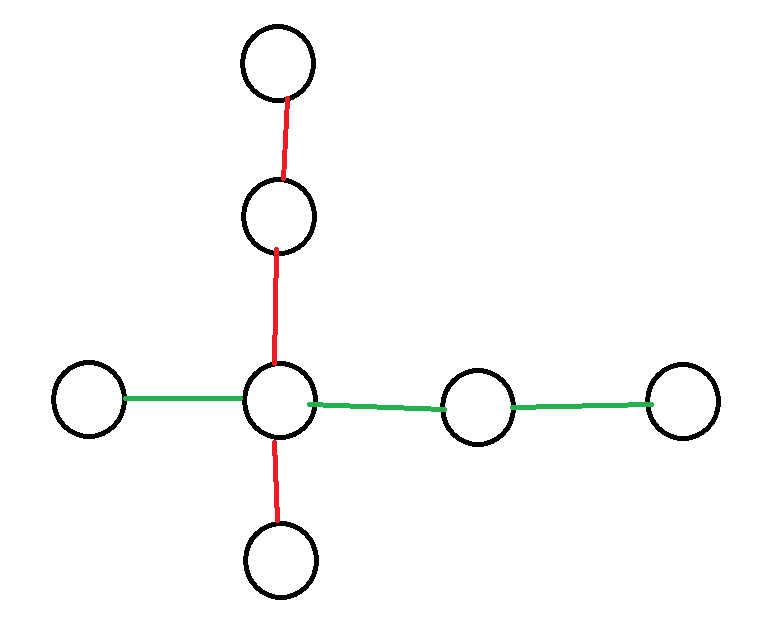
此时这两条路线上的边贡献次数为\(1\),其他的边贡献次数为\(2\)
第二种是不存在公共点的,容易发现最优时这两条路径中间一定存在一条简单边,如图(红色和绿色分别代表一条路径,蓝色是一条简单边)
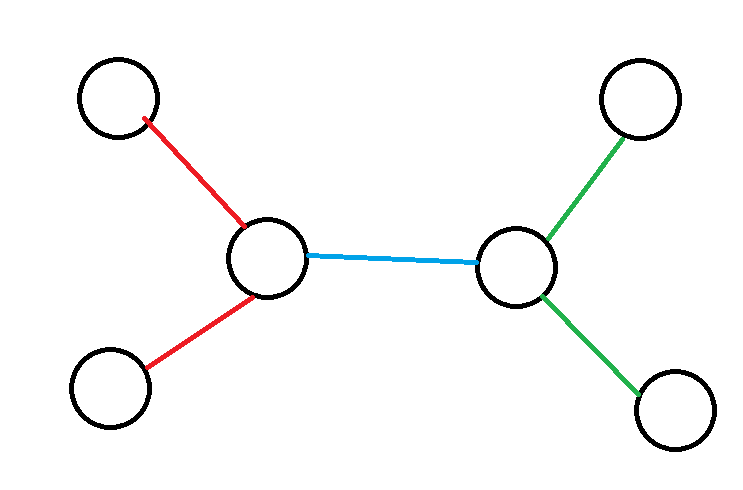
此时这两条路线上的边贡献次数为\(1\),该简单边的贡献次数为\(0\),其它的边贡献次数为\(2\)
考虑用换根DP解决问题,我们设\(f0_i\)表示\(i\)的子树内以\(i\)为端点的最长路径,\(f1_i\)表示\(i\)的子树内经过\(i\)的最长路径
同理\(g0_i,g1_i\)表示子树外的情况,维护信息可以用可删除堆即可,总复杂度\(O(n\log n)\)
刚开始样例挂了好久最后发现把STL堆默认的大根堆记成小根堆了,调了好久
#include<cstdio>
#include<iostream>
#include<vector>
#include<queue>
#define CI const int&
#define RI register int
#define CL const LL
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
typedef long long LL;
typedef pair <int,int> pi;
const int N=100005;
int n,x,y,z; vector <pi> v[N]; LL f0[N],f1[N],g0[N],g1[N],sum,ans;
class Deletable_Heap
{
private:
LL stk[N]; int Tp;
priority_queue <LL> add,del;
public:
inline void clear(void)
{
while (!add.empty()) add.pop(); while (!del.empty()) del.pop();
}
inline void insert(CL x)
{
add.push(x);
}
inline void remove(CL x)
{
del.push(x);
}
inline LL top(void)
{
while (!add.empty()&&!del.empty()&&add.top()==del.top()) add.pop(),del.pop();
return add.empty()?0:add.top();
}
inline void pop(void)
{
if (!add.empty()) stk[++Tp]=add.top(),add.pop();
}
inline void revoke(void)
{
while (Tp) add.push(stk[Tp--]);
}
}S,T;
inline void DFS1(CI now=1,CI fa=0)
{
for (auto [to,w]:v[now]) if (to!=fa)
{
DFS1(to,now); f1[now]=max(f1[now],f0[now]+f0[to]+w);
f1[now]=max(f1[now],f1[to]); f0[now]=max(f0[now],f0[to]+w);
}
}
inline void DFS2(CI now=1,CI fa=0,CL lst=0)
{
S.clear(); T.clear(); S.insert(g0[now]+lst); T.insert(g1[now]);
for (auto [to,w]:v[now]) if (to!=fa)
S.insert(f0[to]+w),T.insert(f1[to]); LL ret=0;
for (RI i=0;i<4;++i) ret+=S.top(),S.pop(); S.revoke(); ans=max(ans,ret);
for (auto [to,w]:v[now]) if (to!=fa)
{
S.remove(f0[to]+w); T.remove(f1[to]);
g0[to]=g1[to]=S.top(); S.pop();
g1[to]+=S.top(); S.revoke(); g1[to]=max(g1[to],T.top());
ans=max(ans,f1[to]+2LL*w+g1[to]);
S.insert(f0[to]+w); T.insert(f1[to]);
}
for (auto [to,w]:v[now]) if (to!=fa) DFS2(to,now,w);
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),i=1;i<n;++i)
scanf("%d%d%d",&x,&y,&z),v[x].pb(mp(y,z)),v[y].pb(mp(x,z)),sum+=2LL*z;
return DFS1(),DFS2(),printf("%lld",sum-ans),0;
}
I. Imitating the Key Tree
巧夺天工(乱用成语)的计数题,仙得不行
首先考虑从零开始生成两个图,每个图都是\(N\)个点,图一最后要有\(2N-2\)条边,图二最后要有\(N-1\)条边并构成Key Tree
考虑对于每个\(k\in[1,2N-2]\)执行如下操作:
- 加入一条边权为\(k\)的边在图一中
- 进行选择,要么在图二中也加入一条边权为\(k\)的边,要么什么都不做
我们首先考虑那些没有在图二中加入的\(k\),称其在图一中对应的边为闲置边,显然对于任一条闲置边,它不能连接任意的两个已经存在一条边接通的双连通分量
否则,我们把在图二中加入的\(k\)在图一中对应的边称为联通边,其满足以下性质:
设这条边在图二中连接的两个连通块为\(c_1,c_2\),则这条边在图一中必须连接两个双连通分量,且它们内部各自的点集包含\(c_1,c_2\)
但这样的话不难发现用一条联通边连接两个双连通分量后新的联通部分就不再是双连通分量了,因此我们还需要引出辅助边的概念
顾名思义,辅助边的作用就是在联通边之前接通两个双连通分量的,目的就是为了让联通边加入后依然满足双连通分量的性质
由于联通边的总数必然是\(N-1\),因此亦需要\(N-1\)条辅助边,因此我们有结论:所有的闲置边必然是辅助边,反之亦然
我们假设对于\(k\)号边是联通边,它在图二中对应连接的两个连通块的大小分别为\(s_1,s_2\),那么显然,它和它的辅助边的选法共有\((s_1\times s_2)^2\)种
考虑在\(2N-2\)条边中分出\(N-1\)个二元组,且满足对于\(i\)号二元组和\(j\)号二元组(\(i<j\)),\(i\)中的后一个元素必须出现在\(j\)中的后一个元素之前
这部分的方案数就是可重全排列的\(\frac{(2N-2)!}{(2!)^{N-1}}\),在除以所有方案中唯一一种合法的\((N-1)!\),即\(\frac{(2N-2)!}{(2!)^{N-1}\times (N-1)!}\)
总复杂度\(O(n\cdot\alpha(n))\)
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005,mod=998244353,inv2=(mod+1)>>1;
int n,fa[N],x,y,sz[N],ans=1;
inline int getfa(CI x)
{
return fa[x]!=x?fa[x]=getfa(fa[x]):x;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d",&n),i=1;i<=n;++i) fa[i]=i,sz[i]=1;
for (i=1;i<n;++i)
{
scanf("%d%d",&x,&y); x=getfa(x); y=getfa(y);
ans=1LL*ans*sz[x]%mod*sz[y]%mod*sz[x]%mod*sz[y]%mod;
fa[x]=y; sz[y]+=sz[x];
}
for (i=n;i<=2*n-2;++i) ans=1LL*ans*i%mod*inv2%mod;
return printf("%d",ans),0;
}
D. Deducing Sortability
终于做完了我的妈呀十三道题……
首先考虑到我们只需要先找出能生成\(n\)个不同数的情形,顺序什么的后面再说
贪心的考虑,从\(1,2,3\cdots\)枚举,对于每个\(k\),求出所有它能生成的数\(k'\),直到找出\(n\)个不同的数
这里有一点注意的是如果对于数\(k\),它能生成的数个数超过了剩下的空缺,那我们优先选大的那些来保证字典序最小
考虑数的变换过程,稍加分析我们发现对于数\(k\),它能变成的数一定形如\(x\times 2^y,x+y=k\and x,y\ge 0\),我们记这样的分解为二元组\((x,y)\)
随后我们发现一个性质,若存在一个\((x,y)\)满足\(x\)为偶数,那么一定存在一个\((x',y')\)使得\(x\times 2^y=x'\times 2^{y'}\)且\(x'+y'\le x+y\)
因此我们可以发现\(x\)只能是奇数,此时显然不会再发生重复的情况,可以直接统计
考虑询问\(P_i\)的本质是什么,其实就是找出最后生成的数中第\(P_i\)小的数,然后找出是谁生成了它,由于上面的性质我们可以很轻松的找出\((x,y)\),因此现在问题就变成怎么找出第\(P_i\)小的数
考虑到若我们给\((x,y)\)稍作变化,将所有二元组的\(x\)的最高有效位(MSB)变换为相同的而不改变\(x\times 2^y\)的值(即将\(x\)乘上\(2^t\)并将\(y\)减去\(t\))
不难发现此时对数的排序就变成了对二元组\((y,x)\)的排序,我们只需要用桶统计出每个\(y\)的个数然后扫一遍即可
具体实现的时候不需要真的做变换,只需要统计出乘上\(2^y\)的数对应的\(x\)的个数,然后在临时拿后面的一些数变过来看看是否要跳到下一个桶即可,具体实现见代码
复杂度\(O(\sqrt n+q)\),据说还有\(n\le 10^{18}\)时的解法,神之又神
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int n,q,p,bkt[N],cnt; long long sum;
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d%d",&n,&q),i=1;n;++i)
{
int cur=(i+1)>>1; bkt[i]=1;
if (cur<=n) sum+=1LL*i*cur,n-=cur;
else --bkt[i-2*n-1],sum+=1LL*i*n,n=0;
}
if (printf("%lld\n",sum),cnt=i-1,cnt>1)
{
for (i=cnt-2;i;--i) bkt[i]+=bkt[i+2];
}
int pfx=0; i=1; while (q--)
{
scanf("%d",&p); while (pfx+bkt[i]*2-1<p) pfx+=bkt[i++];
p-=pfx; int c=__builtin_ctz(p); printf("%d\n",i-1+c+(p>>c));
}
return 0;
}
Postscript
终于,还是完结了……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号