BZOJ 3571: [Hnoi2014]画框

这个算是常见套路题，记得暑假里做过BZOJ2395 time is money，然后发现这两个是一个套路的

首先我们考虑将两维单独考虑，令\(x=\sum_{i=1}^n a_{i,p_i},y=\sum_{i=1}^n b_{i,p_i}\)，那么我们可以把一种匹配方式看作平面上的一个点\((x,y)\)

考虑最后我们所求的答案\(k=xy\)，即\(y=\frac{k}{x}\)，为反比例函数，那么显然我们要找的点肯定在靠近原点的下凸壳上

既然这样，我们不妨找出位于凸壳上的两点\(A,B\)，\(A\)满足\(\sum_{i=1}^n a_{i,p_i}\)最小，\(B\)满足\(\sum_{i=1}^n b_{i,p_i}\)最小

然后我们作出线段\(AB\)，考虑在靠近原点的一侧找一个点\(C\)，使得这个点离原点尽量近

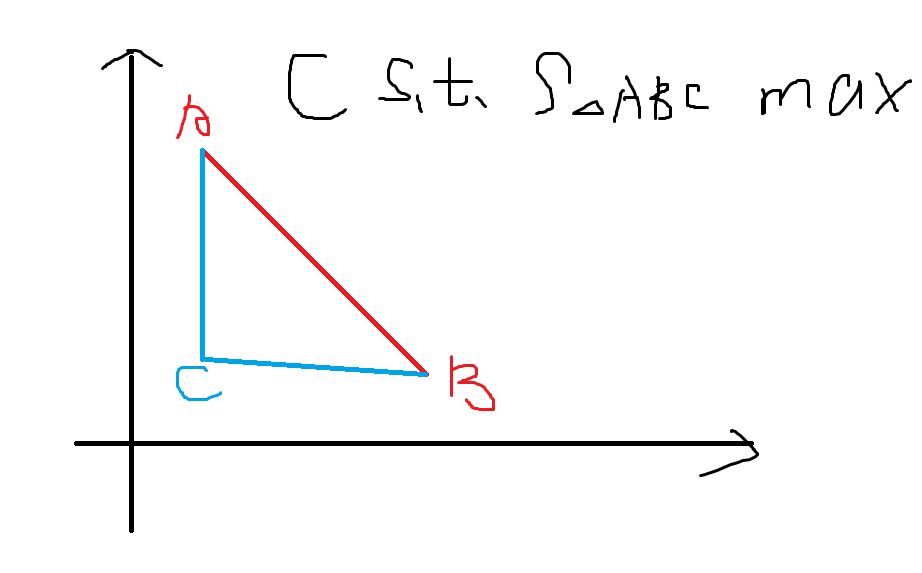
那么此时显然\(C\)满足\(S_{\triangle ABC} \max\)，换句话说就是\(\vec{AB}\times \vec{AC}\min\)（因为是负的）

考虑我们展开它:

\[\vec{AB}\times \vec{AC}\\=(B_x-A_x)\times(C_y-A_y)-(B_y-A_y)\times (C_x-A_x)\\=(A_y-B_y)\times C_x+(B_x-A_x)\times C_y+\cdots \]

其中\(\cdots\)都是只与\(A,B\)有关的项，因此我们再找出满足\((A_y-B_y)\times C_x+(B_x-A_x)\times C_y\)最小的点\(C\)

可是\(C\)也不一定是最优的啊，没事我们发现此时我们又有了两条线段\(AC,CB\)，直接递归下去做就好了

边界显然是找不到这样的\(C\)点，即\(\vec{AB}\times \vec{AC}\ge 0\)

然后找到这样的点的过程显然就是个最大权匹配，直接上KM即可，复杂度\(O(\text{很快})\)

#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=150,INF=1e9;
struct point
{
	int x,y;
	inline point(CI X=0,CI Y=0) { x=X; y=Y; }
}; int t,n,w[N][N],a[N][N],b[N][N],ans;
inline point operator - (const point& A,const point& B)
{
	return point(A.x-B.x,A.y-B.y);
}
inline int Cross(const point& A,const point& B)
{
	return A.x*B.y-A.y*B.x;
}
namespace KM
{
	int dx[N],dy[N],rsd[N],fr[N]; bool vx[N],vy[N];
	inline void build(CI rx,CI ry)
	{
		for (RI i=1,j;i<=n;++i) for (j=1;j<=n;++j)
		w[i][j]=-(rx*a[i][j]+ry*b[i][j]);
	}
	inline bool find(CI now)
	{
		vx[now]=1; for (RI to=1;to<=n;++to) if (!vy[to])
		{
			int dlt=dx[now]+dy[to]-w[now][to];
			if (!dlt) { vy[to]=1; if (!~fr[to]||find(fr[to])) return fr[to]=now,1; }
			else rsd[to]=min(rsd[to],dlt);
		}
		return 0;
	}
	inline point KM(void)
	{
		RI i,j; for (i=1;i<=n;++i) fr[i]=-1,dx[i]=-INF,dy[i]=0;
		for (i=1;i<=n;++i) for (j=1;j<=n;++j) dx[i]=max(dx[i],w[i][j]);
		for (i=1;i<=n;++i)
		{
			for (j=1;j<=n;++j) rsd[j]=INF; for (;;)
			{
				for (j=1;j<=n;++j) vx[j]=vy[j]=0; if (find(i)) break;
				int dlt=INF; for (j=1;j<=n;++j) if (!vy[j]) dlt=min(dlt,rsd[j]);
				for (j=1;j<=n;++j) if (vx[j]) dx[j]-=dlt;
				for (j=1;j<=n;++j) if (vy[j]) dy[j]+=dlt; else rsd[j]-=dlt;
			}
		}
		point ret; for (i=1;i<=n;++i) ret.x+=a[fr[i]][i],ret.y+=b[fr[i]][i]; return ret;
	}
};
inline void solve(const point& A,const point& B)
{
	KM::build(A.y-B.y,B.x-A.x); point C=KM::KM(); ans=min(ans,C.x*C.y);
	if (Cross(B-A,C-A)>=0) return; solve(A,C); solve(C,B);
}
int main()
{
	for (scanf("%d",&t);t;--t)
	{
		RI i,j; for (scanf("%d",&n),i=1;i<=n;++i) for (j=1;j<=n;++j)
		scanf("%d",&a[i][j]); for (i=1;i<=n;++i) for (j=1;j<=n;++j)
		scanf("%d",&b[i][j]); point A,B;
		KM::build(1,0); A=KM::KM(); KM::build(0,1); B=KM::KM();
		ans=min(A.x*A.y,B.x*B.y); solve(A,B); printf("%d\n",ans);
	}
	return 0; 
}