BZOJ 3670: [Noi2014]动物园

现在看来真是自然无比。。。

首先我们先求出\(next\)数组，然后不考虑那个不重叠的限制

换句话说现在可以搞一个\(num'\)出来，容易发现对于一个前缀\(i\)的\(next_i\)它满足题目的要求，同时\(next_{next_i}\)显然也是满足的，再往下推同理

然后我们发现\(num'\)数组可以和\(next\)数组一起递推出来，非常方便，那么现在就是怎么求\(num\)的问题了

随手画个图，假设我们现在对于位置\(i\)用\(next\)向前跳，直到跳到第一个位置\(j\)满足\(j\le\lfloor \frac{i}{2}\rfloor\)，那么这个时候应该是这样：

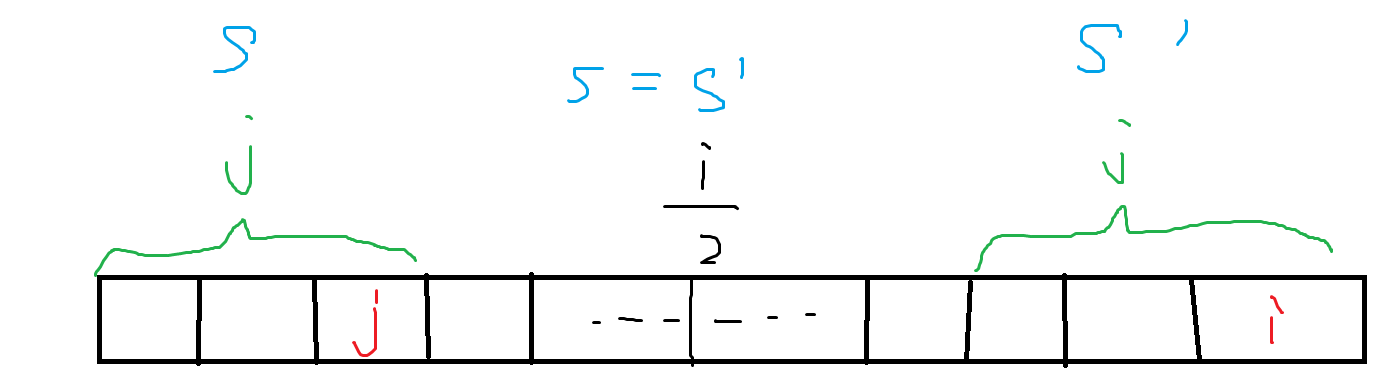
此时显然从\(j\)开始往前跳\(next\)的串都满足要求，并且\(num'_j=num_i\)（因为不会重复了，\(j\)的前缀已经和\(i\)的后缀相同）

然后就做完了，复杂度\(O(n)\)

#include<cstdio>
#include<cstring>
using namespace std;
const int N=1000005,mod=1e9+7;
char s[N];
int n,next[N],num[N],ans,t;
inline void get_next(char *s)
{
	register int i; int len=0;
	for (i=2;i<=n;++i)
	{
		while (len&&s[i]!=s[len+1]) len=next[len];
		if (s[i]==s[len+1]) ++len; next[i]=len; num[i]=num[len]+1;
	}
}
inline void get_num(char *s)
{
	register int i; int len=0;
	for (i=2;i<=n;++i)
	{
		while (len&&s[i]!=s[len+1]) len=next[len];
		if (s[i]==s[len+1]) ++len;
		while ((len<<1)>i) len=next[len];
		ans=1LL*ans*(num[len]+1)%mod;
	}
}
int main()
{
	scanf("%d",&t); while (t--)
	{
		scanf("%s",s+1); n=strlen(s+1); ans=1;
		memset(next,0,sizeof(next)); num[1]=1;
		get_next(s); get_num(s); printf("%d\n",ans);
	}
	return 0;
}