机器学习一到三章笔记

机器学习第一到三章学习笔记

1.1什么是模式识别

定义：模式识别是根据已有的知识表达，针对待识别模式，判别决策其所属的类别或者预测其对应的回归值。

应用领域：计算机视觉，人机交互，医学，网络，金融，机器人，无人车。

1.2模式识别数学表达

1. 数学解释：看成一种函数映射f(x),将待识别模式x从输入空间映射到输出空间，f(x)是关于已有知识的表达。

2. 模型：关于已有知识的一种表达方式，即函数f(x)

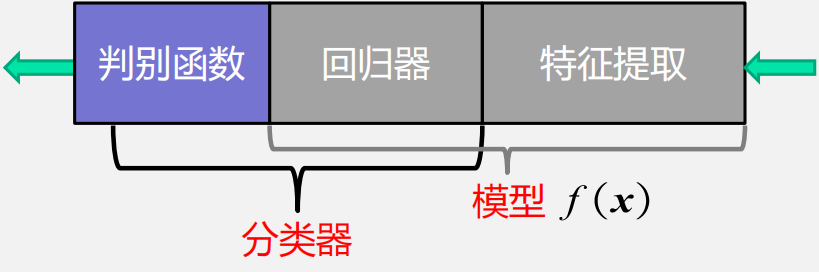
3. 判别函数分类

二类分类：使用sign函数判别大于0还是小于0
多类分类（max函数）：取最大的回归值所在的维度对应的类别
4.特征
- 用于区分不同类别模式、可测量的量
- 特征要具有辨别能力、鲁棒性

1.3特征向量的相关性

1.点积、夹角，投影

1.4机器学习的基本概念

1.线性模型（直线、面、超平面）：y=w^Tx+w0 适用于线性可分的数据

2.常见非线性模型：多项式，神经网络，决策树

3.训练样本个数N与模型参数M的关系
- N=M:参数有唯一解
- N>>M:没有准确的解（over-determined）
- N<<M:无数个解/无解

4.目标函数（对于over-determined情况）：通过优化该标准来确定一个近似解

优化算法：最小化或最大化目标函数的技术

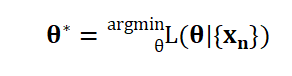
流程

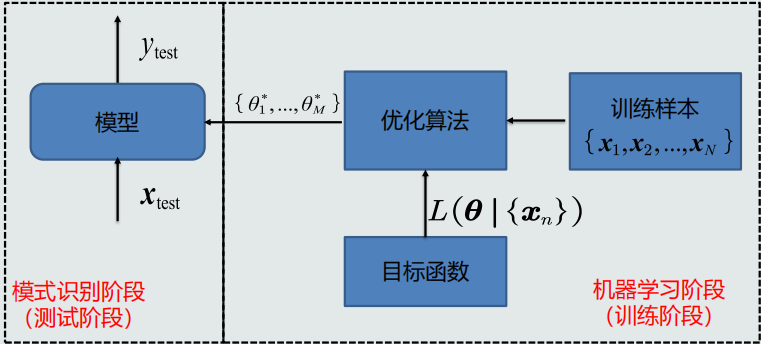
5.真值（标签）&标注：我们把有提供真值Tn的样本称为标注过的样本

监督学习：训练样本xn与输出真值tn都给定，以最小化训练误差为目标函数

给定{x1,x2,…,xN}和{t1,t2,…,tN}，求解{θ1,θ2,…,θM}

最小化训练误差目标函数：
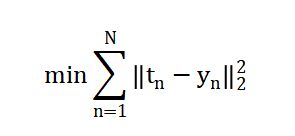
无监督学习：给训练样本，没有给真值
聚类：
强化学习：机器自行探索决策、真值滞后反馈的过程。

1.5模型的泛化能力

1.训练集(training set)：集合中的每个样本称作训练样本

2.测试集（test set）:集合中的测试样本

3.验证集（validation set)：基于该集合调整超参数

4.训练误差(training error）：模型在训练集上的误差，测试误差（test error）：模型在测试集上的误差。它反映了模型的泛化能力，也称作泛化误差。

5.训练样本可能存在训练样本稀疏，采样过程不均匀，带有噪声的问题

过拟合：模型训练阶段好，测试表现差，过于拟合训练数据

6.泛化能力：训练得到的模型不仅要对训练样本具有决策能力，也要对新的（训练过程中未看见）的模式具有决策能力。

7.提高泛化能力：不要过度训练。可以采用（1）选择复杂度适合的模型（2）在目标函数中加入正则项来实现

1.6评估方法与性能指标

1.留出法：将数据集随机分为两组：训练集和测试集。

2.K折交叉验证：将数据集分割K个子集，从其中选取单个子集作为测试集，其他K-1个子集作为训练集，交叉验证重复K次，使每个子集都被测试一次，将K次的评估值去平均作为结果。

3.留一验证：每次只取数据集中的一个样本做测试集，剩余的做训练集，每个样本测试一次，取所有评估值的平均值作为最终评估结果。

4.性能指标：

二类分类中

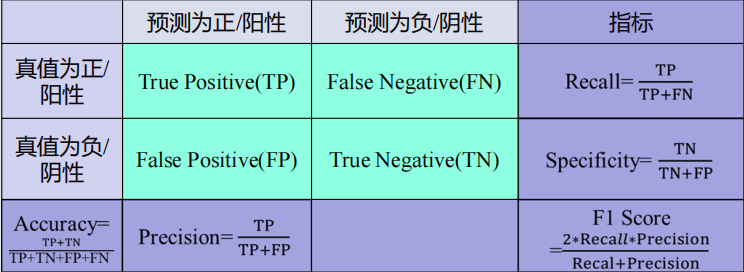
混淆矩阵(Confusion Matrix)
- 列为预测值，行为真值，对角线是正确分类的统计值（越大越好）
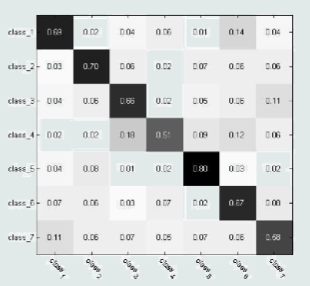
- PR与ROC与AUC

2.1 MED分类器

1.基于距离的决策：把测试样本到每个类之间的距离作为决策模型，将测试样本判定为与其距离最近的类。

2.原型的种类：均值——将该类中所有训练样本的均值作为类的原型。最近邻——从一类的训练样本中，选取与测试样本距离最近的一个训练样本，作为该类的原型。

3.距离的种类：欧式距离，曼哈顿距离，加权欧式距离。

4.MED分类器：最小欧式距离分类器，类的原型为均值。

存在的问题：MED分类器采用欧氏距离作为距离度量，没有考虑特征变化的不同及特征之间的相关性。
解决方法：特征白化

import pandas as pd
from sklearn.model_selection import train_test_split
from scipy.spatial.distance import euclidean
import numpy as np

import ai_utils

DATA_FILE = './data_ai_practice/fruit_data.csv'
FRUIT_NAME = ['apple','mandarin','orange','lemon']
FEAT_COLS = ['mass','width','height','color_score']


def get_pred_label(test_sample_feat,train_data):
    """
         “近朱者赤” 找最近距离的训练样本，取其标签作为预测样本的标签
    """
    dis_lis =[]

    for idx,row in train_data.iterrows():
        #训练样本特征
        train_sample_feat = row[FEAT_COLS].values

        #计算距离
        dis = euclidean(test_sample_feat,train_sample_feat)
        dis_lis.append(dis)

    #最小距离对应的位置
    pos = np.argmin(dis_lis)
    pred_label = train_data.iloc[pos]['fruit_name']
    return pred_label

def main():
    """
    主函数

    """
    #读取数据集
    fruit_data = pd.read_csv(DATA_FILE)

    #划分数据集
    train_data,test_data=train_test_split(fruit_data,test_size=1/5,random_state=10)

    #预测对的个数
    acc_count = 0

    #分类器
    for idx,row in test_data.iterrows():
        #测试样本特征
        test_sample_feat = row[FEAT_COLS].values

        #预测值
        pred_label = get_pred_label(test_sample_feat,train_data)

        #真实值
        true_label = row['fruit_name']

        print('样本{}的真实标签{}，预测标签{}'.format(idx,true_label,pred_label))

        if true_label == pred_label:
            acc_count += 1

    #准确率
    accuracy = acc_count/test_data.shape[0]
    print('预测准确率{:.2f}%'.format(accuracy*100))

if __name__ == '__main__':
    main()

2.2特征白化：去除特征相关性

1.特征白化的目的：将原始特征映射到新的一个特征空间，使得在新空间中特征的协方差为单位矩阵，从而去除特征变化的不同及特征之间的相关性。

2.特征转化的过程：将特征转化分为两步：先去除特征之间的相关性（解耦），然后再对特征进行尺度变化（白化）。令W=W1W2，解耦：通过W1实现协方差矩阵对角化，去除特征之间的相关性。白化：通过W2对上一步变换后的特征再进行尺度变换实现所有特征具有相同方差。

W1起到旋转的作用

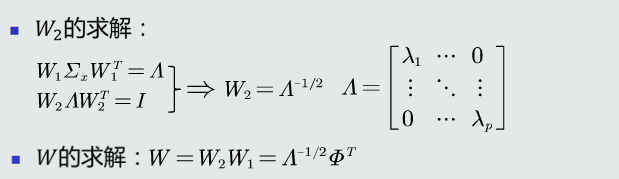
3.W转换后的欧式距离发生改变，变成马氏距离

2.3 MICD分类器

1.MICD分类器：最小类内距离分类器，基于马氏距离的分类器。类的原型：均值.

MICD分类器的缺陷是会选择方差较大的那一类。优点是不受量纲的影响.

3.1贝叶斯决策与MAP分类器

1.后验概率：给定一个测试模式x，决策其属于哪个类别需要依赖于P(Ci|x)，该表达式称为后验概率，表达给定模式x属于类Ci的可能性。

2.在已知先验概率和观测概率的情况下：

3.MAP分类器：最大后验概率分类器，将测试样本决策分类给后验概率最大的那个类，等同于最小化平均概率误差，即最小化决策误差。

3.2 MAP分类器：高斯观测概率

1.表达先验和观测概率的方式

	- 常数表达
	- 参数化解析表达
	- 非参数化表达：直方图，核密度，蒙特卡洛

2.若观测似然概率为一维高斯分布。在方差相同的情况，分类器决策偏向先验概率高的类。方差不同且先验概率相同时，分类器倾向于选择方差较小的类。

3.3决策风险与贝叶斯分类器

1.决策风险：不同的错误决策产生完全不一样的风险。

2.损失：表征当前决策动作相对于其他候选类别的风险程度

3.决策风险的评估：给定一个测试样本x，分类器决策其属于Ci类的动作对于的决策风险可以定义为相对于所有候选类别的期望损失。

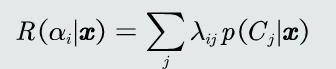
4.贝叶斯分类器：在MAP分类器基础上，加入决策风险因素，得到贝叶斯分类器。贝叶斯分类器选择决策风险最小的类，即最小化期望损失。

5.朴素贝叶斯分类器：当特征是多维的，假设特征之间是相互独立的，从而得到以下公式

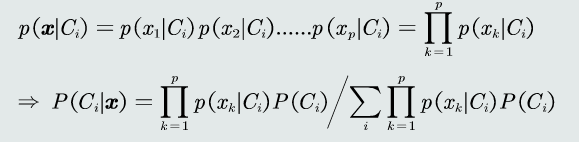
6.拒绝选项：当测试数据在决策边界时，即使选择后验概率高的，该概率的值仍然可能很小。为了避免错误决策，引入阈值，当概率低于阈值时不决策

import numpy as np 
import math
# 使用词集法进行贝叶斯分类
# 构造数据集,分类是侮辱性 or 非侮辱性
def loadDataset () :
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]    #1 is abusive, 0 not
    return postingList, classVec


# 创建一个包涵所有词汇的列表 , 为后面建立词条向量使用
def createlist (dataset) :
    vovabset = set ([])
    for vec in dataset :
        vovabset = vovabset | set (vec)
    return list (vovabset)

# 将词条转化为向量的形式
def changeword2vec (inputdata, wordlist) :
    returnVec = [0] * len (wordlist)
    for word in inputdata :
        if word in wordlist :
            returnVec[wordlist.index(word)] = 1
    return returnVec

# 创建贝叶斯分类器 
def trainNBO (dataset, classlebels) :
    num_of_sample = len (dataset)
    num_of_feature = len (dataset[0])
    pAusuive = sum (classlebels) / num_of_sample # 侮辱性语言的概率
    p0Num = np.ones (num_of_feature)
    p1Num = np.ones (num_of_feature)
    p0tot = num_of_feature
    p1tot = num_of_feature
    for i in range (num_of_sample) :
        if classlebels[i] == 1 :
            p1Num += dataset[i]
            p1tot += sum (dataset[i])
        else :
            p0Num += dataset[i]
            p0tot += sum (dataset[i])   
    p0Vec = p0Num / p0tot
    p1Vec = p1Num / p1tot
    for i in range (num_of_feature) :
        p0Vec[i] = math.log (p0Vec[i])
        p1Vec[i] = math.log (p1Vec[i])
    return p0Vec, p1Vec, pAusuive


#  定义分类器 
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)    #element-wise mult
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else: 
        return 0

# 测试代码 
dataset,classlebels = loadDataset ()
wordlist = createlist (dataset)
print (wordlist)
print (changeword2vec (dataset[0], wordlist))
trainmat = []
for temp in dataset :
    trainmat.append (changeword2vec (temp,wordlist))
p0V, p1V, pAb = trainNBO (trainmat, classlebels)
print (p0V)
print (p1V)
print (pAb)