[NOIP2017]逛公园
题面在这里
description
策策同学特别喜欢逛公园。
公园可以看成一张\(N\)个点\(M\) 条边构成的有向图，且没有自环和重边。
其中\(1\)号点是公园的入口，\(N\)号点是公园的出口，
每条边有一个非负权值，代表策策经过这条边所要花的时间。
策策每天都会去逛公园，他总是从\(1\)号点进去，从\(N\)号点出来。
策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个 特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。
如果\(1\)号点到\(N\)号点的最短路长为\(d\),那么策策只会喜欢长度不超过\(d+K\) 的路线。
策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？
为避免输出过大，答案对\(P\)取模。
如果有无穷多条合法的路线，请输出\(−1\)。
data range
\[1\le N\le 100000,1\le M\le 200000,1\le k\le 50
\]
\[1 \le P \le 10^9,1 \le a_i,b_i \le N ,0 \le c_i \le 1000,1≤P≤10^9
\]
solution
时隔近一年终于改掉了这道题
还是卡着时间AC的
30pts:最短路计数
在跑\(SPFA\)更新最短路的同时更新最短路的数量,
具体来说,如果最短路要更新就把其数量重置为其前驱最短路的数量，
如果最短路的值不变那么其数量叠加
但是这样是可能存在问题的
比如下面这张图
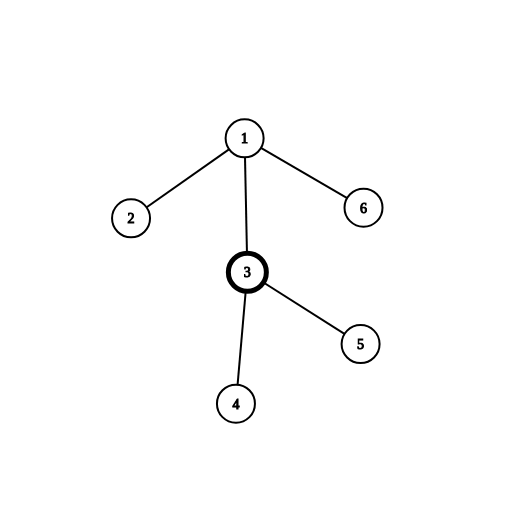
如果点2比点4先入队的话，
点3的最短路条数就会在第一次取出点2的时候更新一次，
点4的入队会导致点2第二次入队，那么点4又会被点2更新一次;
第一次更新时点2最短路条数为1,第二次更新时点2最短路条数为2
两次相加点4的最短路条数就是3,明显不对
于是我们需要改进我们的\(SPFA\)
笔者的做法是这样的:
我们记录一个\(top\)值表示当前节点最后一次更新的时候存的最短路条数,
在一次转移完成之后\(top=f\),转移的时候使用\(f-top\)转移,这样就不会算重啦
il void spfa(bool s){//s代表是否需要统计最短路
memset(f,0,sizeof(f));
memset(t,0,sizeof(t));
while(!Q.empty())Q.pop();
for(RG int i=1;i<=n;i++)dis[i]=inf,vis[i]=0;
vis[1]=1;dis[1]=0;Q.push(1);f[1][0]=1;
while(!Q.empty()){
RG int u=Q.front();Q.pop();
for(RG int i=head[u];i;i=nxt[i]){
RG int v=to[i];
if(!s){
if(dis[v]>dis[u]+val[i]){
dis[v]=dis[u]+val[i];
if(!vis[v]){
Q.push(v);vis[v]=1;
}
}
}
else{
if(dis[v]>=dis[u]+val[i]){
if(dis[v]>dis[u]+val[i]){
dis[v]=dis[u]+val[i];
f[v][0]=f[u][0];t[v]=0;
}
else if(dis[v]==dis[u]+val[i]){
(f[v][0]+=(f[u][0]-t[u]+p)%p)%=p;
}
if(!vis[v]){
Q.push(v);vis[v]=1;
}
}
}
}
vis[u]=0;t[u]=f[u][0];
}
}
60pts:DP
\(DP\)方程式是显然的,设\(f[k][u]\)表示点\(1\)到达\(u\)路径长度为\(dis[u]+k\)的方案数,
那么转移的途径只能是边对吧?
\[f[k][u]-_{each\ e(u,v)}>f[k+dis[u]+val[e]-dis[v]][v]
\]
但是我们在\(DP\)的时候之前的\(f\)必须已经被计算好了,怎么办呢?
试想一个点只可能由\(dis\)比它小的点转移而来
因此我们需要从$ $最小的开始枚举边进行转移,这样就不会出问题啦
il void DP(){//DP.
for(RG int j=0;j<=k;j++)
for(RG int s=1;s<=n;s++){
RG int u=P[s].id;
for(RG int i=head[u];i;i=nxt[i]){
RG int v=to[i];
if(dis[u]+j+val[i]-dis[v]>0&&dis[u]+j+val[i]-dis[v]<=k)
(f[v][dis[u]+j+val[i]-dis[v]]+=f[u][j])%=p;
}
}
}
100pts:
\(0\)边真是个恐怖的存在,\(0\)环更不用说了;其实0边还好
首先我们考虑侥幸不存在\(0\)环的情况,如图所示:
这里我们的最短路计数不会出问题,但是$ \(都相等,
直接按照\) \(确定顺序的话可能会\)WA\(
由于我们对于这些点\)DP$的顺序和其在\(0\)边连接下的拓补序有关,
我们考虑把所有\(0\)边都加入一个新图,然后做一遍拓补排序即可
那如果有\(0\)环怎么办呢?
我们考虑一个\(0\)环什么时候才会影响到答案，
即是这个环上任意一点被算在了一条可行的路径中,
那么我们处理出\(dis\)和\(fdis(反图中点n的最短路)\),
由于不会存在负环,最短路是不会出现问题的;
在\(0\)环上的任意一点\(i\)满足\(dis[i]+fdis[i]\le dis[n]+k\)就可以输出\(-1\)了
code
#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<iomanip>
#include<cstring>
#include<complex>
#include<vector>
#include<cstdio>
#include<string>
#include<bitset>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<set>
//#define TEST
#define FILE "park"
#define mp make_pair
#define pb push_back
#define RG register
#define il inline
using namespace std;
typedef unsigned long long ull;
typedef vector<int>VI;
typedef long long ll;
typedef double dd;
const int inf=1e9+7;
const int mod2=998244353;
const int rev2=332748118;
const int mod1=1e9+7;
const int N=100010;
const dd eps=1e-10;
const ll INF=1e18;
const int g=3;
il ll read(){
RG ll data=0,w=1;RG char ch=getchar();
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(ch<='9'&&ch>='0')data=data*10+ch-48,ch=getchar();
return data*w;
}
il void file(){
freopen(FILE".in","r",stdin);
freopen(FILE".out","w",stdout);
}
int n,m,k,p,ans;
int head[N],nxt[N<<1],to[N<<1],val[N<<1],cnt;
il void add(int u,int v,int w){
to[++cnt]=v;
nxt[cnt]=head[u];
val[cnt]=w;
head[u]=cnt;
}
int fhead[N],fnxt[N<<1],fto[N<<1],fval[N<<1],fcnt;
il void fadd(int u,int v,int w){
fto[++fcnt]=v;
fnxt[fcnt]=fhead[u];
fval[fcnt]=w;
fhead[u]=fcnt;
}
int zhead[N],znxt[N<<1],zto[N<<1],zd[N],zcnt;
il void zadd(int u,int v){
zto[++zcnt]=v;zd[v]++;
znxt[zcnt]=zhead[u];
zhead[u]=zcnt;
}
queue<int>Q;bool vis[N];int dis[N],f[N][52],t[N];
il void spfa(bool s){//s代表是否需要统计最短路
memset(f,0,sizeof(f));
memset(t,0,sizeof(t));
while(!Q.empty())Q.pop();
for(RG int i=1;i<=n;i++)dis[i]=inf,vis[i]=0;
vis[1]=1;dis[1]=0;Q.push(1);f[1][0]=1;
while(!Q.empty()){
RG int u=Q.front();Q.pop();
for(RG int i=head[u];i;i=nxt[i]){
RG int v=to[i];
if(!s){
if(dis[v]>dis[u]+val[i]){
dis[v]=dis[u]+val[i];
if(!vis[v]){
Q.push(v);vis[v]=1;
}
}
}
else{
if(dis[v]>=dis[u]+val[i]){
if(dis[v]>dis[u]+val[i]){
dis[v]=dis[u]+val[i];
f[v][0]=f[u][0];t[v]=0;
}
else if(dis[v]==dis[u]+val[i]){
(f[v][0]+=(f[u][0]-t[u]+p)%p)%=p;
}
if(!vis[v]){
Q.push(v);vis[v]=1;
}
}
}
}
vis[u]=0;t[u]=f[u][0];
}
}
int fdis[N];
il void fspfa(){
while(!Q.empty())Q.pop();
for(RG int i=1;i<=n;i++)fdis[i]=inf,vis[i]=0;
vis[1]=1;fdis[n]=0;Q.push(n);
while(!Q.empty()){
RG int u=Q.front();Q.pop();
for(RG int i=fhead[u];i;i=fnxt[i]){
RG int v=fto[i];
if(fdis[v]>fdis[u]+fval[i]){
fdis[v]=fdis[u]+fval[i];
if(!vis[v]){
Q.push(v);vis[v]=1;
}
}
}
vis[u]=0;
}
}
bool inz[N],incal[N];int dfn[N],low[N],tott,cal[N],top;
il void tarjan(int u){//check 0-circle
dfn[u]=low[u]=++tott;incal[cal[++top]=u]=1;
for(RG int i=zhead[u];i;i=znxt[i]){
RG int v=zto[i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(incal[v])low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
if(cal[top]==u){incal[cal[top--]]=0;return;}
while(cal[top]!=u){
incal[cal[top]]=0;inz[cal[top]]=1;top--;
}
incal[cal[top]]=0;inz[cal[top]]=1;top--;
}
}
struct node{int id,dis,zt;}P[N];
bool cmp(node x,node y){
return x.dis==y.dis?x.zt<y.zt:x.dis<y.dis;
}
int totz;
il void bfs_z(){//tuopu 0 dag,make a order
while(!Q.empty())Q.pop();
for(RG int i=1;i<=n;i++)
if(!zd[i])Q.push(i);
while(!Q.empty()){
RG int u=Q.front();Q.pop();P[u].zt=++totz;
for(RG int i=zhead[u];i;i=znxt[i]){
RG int v=zto[i];
if(!(--zd[v]))Q.push(v);
}
}
}
il void DP(){//DP.
for(RG int j=0;j<=k;j++)
for(RG int s=1;s<=n;s++){
RG int u=P[s].id;
for(RG int i=head[u];i;i=nxt[i]){
RG int v=to[i];
if(dis[u]+j+val[i]-dis[v]>0&&dis[u]+j+val[i]-dis[v]<=k)
(f[v][dis[u]+j+val[i]-dis[v]]+=f[u][j])%=p;
}
}
}
il void solve(){
n=read();m=read();k=read();p=read();
memset(head,0,sizeof(head));cnt=0;
memset(fhead,0,sizeof(fhead));fcnt=0;
memset(zhead,0,sizeof(zhead));zcnt=0;
memset(zd,0,sizeof(zd));
for(RG int i=1,u,v,w;i<=m;i++){
u=read();v=read();w=read();
if(!w)zadd(u,v);add(u,v,w);fadd(v,u,w);
}
spfa(0);fspfa();
memset(inz,0,sizeof(inz));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));tott=0;
for(RG int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
for(RG int i=1;i<=n;i++)
if(inz[i]&&dis[i]+fdis[i]<=dis[n]+k){
puts("-1");return;
}
//-1
spfa(1);
totz=ans=0;bfs_z();
for(RG int i=1;i<=n;i++){
P[i].id=i;P[i].dis=dis[i];
}
sort(P+1,P+n+1,cmp);
DP();
for(RG int i=0;i<=k;i++)(ans+=f[n][i])%=p;
printf("%d\n",ans);
//DP
}
int main()
{
RG int T=read();while(T--)solve();return 0;
}
