DFS序例题+感受(已更新到6题)
最近在学dfs序的实际应用,专开个blog记录下感受
目前来看都是配合线段树,从树上问题变成区间问题,顺便吐槽下有些人的题集竟然不挂链接
求和
https://ac.nowcoder.com/acm/problem/204871
题面:
已知有 \(n\) 个节点,有 \(n - 1\) 条边,形成一个树的结构。
给定一个根节点 \(k\),每个节点都有一个权值,节点 \(i\) 的权值为 \(v_i\)。
给 \(m\) 个操作,操作有两种类型:
1 \(ax\):表示将节点 \(a\) 的权值加上 \(x\)
2 \(a\):表示求 \(a\) 节点的子树上所有节点的和(包括 \(a\) 节点本身
输入:
第一行给出三个正整数 \(n, m, k\),表示树的节点数、操作次数、和这棵树的根节点。
第二行给出 \(n\) 个正整数,第 \(i\) 个正整数表示第 \(i\) 个节点的权值 \(val_i\)。
下面 \(n - 1\) 行每行两个正整数 \(u, v\),表示边的两个端点。
接下来 \(m\) 行,每行给出一个操作。
输出:
对于每个类型为 2 的操作,输出一行一个正整数,表示以a为根的子树的所有节点的权值和
数据范围:
\(
\begin{align*}
1 &\leq n, m \leq 1e6, 1 \leq k \leq n \\
1 &\leq u, v \leq n \\
1 &\leq a \leq n \\
-1e6 &\leq val_i, x \leq 1e6
\end{align*}
\)
样例:
5 6 1
1 2 3 4 5
1 3
1 2
2 4
2 5
1 2 10
1 3 10
1 4 5
1 5 1
2 3
2 2
————————
13
27
感受:算是个很基本的入门题了,就是dfs序+线段树(单点修改+区间查询),直接一遍过了
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
//#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
struct s
{
ll v,l,r;
ll lazy;
}p[1000002<<2];
void build(ll i,ll l,ll r)
{
p[i].v=0;
p[i].l=l,p[i].r=r;
if(l==r)
return ;
build(i<<1,l,(l+r)>>1);
build(i<<1|1,(l+r>>1)+1,r);
}
void update(ll i,ll l,ll r,ll v)
{
if(l==p[i].l&&r==p[i].r)
{
p[i].v+=v;
return ;
}
ll mid=(p[i].l+p[i].r)>>1;
if(l<=mid)
update(i<<1,l,min(mid,r),v);
if(r>=mid+1)
update(i<<1|1,max(mid+1,l),r,v);
p[i].v=p[i<<1].v+p[i<<1|1].v;
}
ll query(ll i,ll l,ll r)
{
ll ans=0;
if(l==p[i].l&&r==p[i].r)
{
ans+=p[i].v;
return ans;
}
ll mid=(p[i].l+p[i].r)>>1;
if(l<=mid)
ans+=query(i<<1,l,min(mid,r));
if(r>=mid+1)
ans+=query(i<<1|1,max(mid+1,l),r);
return ans;
}
ll a[1000002];
ll ne[2000002];
ll to[2000002];
ll h[2000002];
ll b[2000002];
ll cnt=0;
ll gs=0;
void add(ll l,ll r)
{
to[cnt]=r;
ne[cnt]=h[l];
h[l]=cnt++;
}
void dfs(ll k,ll fa)
{
gs++;
b[gs]=k;
for(ll i=h[k];i>=0;i=ne[i])
{
if(to[i]==fa)continue;
dfs(to[i],k);
}
gs++;
b[gs]=k;
}
ll vis[2000002];
pair<ll,ll>ans[1000002];
int main()
{
fio();
ll n,m,k;
cin>>n>>m>>k;
for(ll i=1;i<=n;i++)cin>>a[i];
memset(h,-1,sizeof h);
build(1,1,n);
for(ll i=1;i<=n-1;i++)
{
ll l,r;
cin>>l>>r;
add(l,r);
add(r,l);
}
dfs(k,0);
cnt=0;
ll last=0;
for(ll i=1;i<=gs;i++)
{
if(vis[b[i]]==0)
{
cnt++;
update(1,cnt,cnt,a[b[i]]);
vis[b[i]]=cnt;
last=cnt;
}
else
{
ans[b[i]]={vis[b[i]],last};
}
}
//cout<<query(1,1,5)<<endl;
while(m--)
{
ll op;
cin>>op;
switch(op)
{
case 1:
{
ll x,y;
cin>>x>>y;
update(1,vis[x],vis[x],y);
break;
}
case 2:
{
ll x;
cin>>x;
cout<<query(1,ans[x].first,ans[x].second)<<endl;
break;
}
}
}
}
Apple Tree
http://poj.org/problem?id=3321
题面:
在卡卡家外面有一棵苹果树。每到秋天,树上就会结出很多苹果。卡卡非常喜欢苹果,所以他一直在精心培育这棵大苹果树。
这棵树有N个分叉,这些分叉通过树枝相连。卡卡用1到N的数字给分叉编号,根分叉总是编号为1。苹果会生长在分叉上,而同一个分叉上不会同时长出两个苹果。卡卡想知道一个子树上有多少个苹果,以研究苹果树的产量。
问题是,一个新的苹果可能随时会在空分叉上生长出来,卡卡也可能为了他的甜点从树上摘一个苹果。你能帮帮卡卡吗?
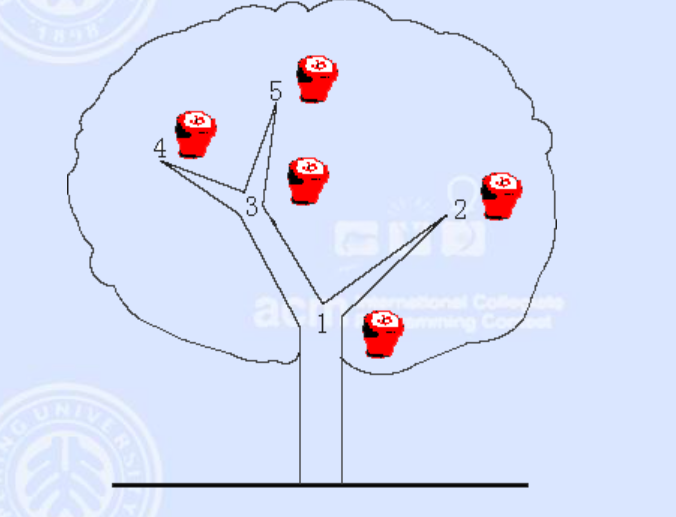
输入:
第一行包含一个整数N(N ≤ 100,000),表示树的分叉数。
接下来的N - 1行每行包含两个整数u和v,意味着分叉u和分叉v通过一个树枝相连。
下一行包含一个整数M(M ≤ 100,000)。
接下来的M行每行包含一个消息,消息是以下两种之一:
"C x" 表示分叉x上苹果的存在状态已经改变。即如果分叉上有苹果,那么卡卡就摘走了它;否则,一个新苹果在空分叉上生长。
或者
"Q x" 表示询问分叉x上方子树上的苹果数量,包括分叉x上存在的苹果(如果存在)。
注意,树最初是满苹果的。
输出:
样例:
3
1 2
1 3
3
Q 1
C 2
Q 1
——————
3
2
思路:写法与上道题一样,但是POJ好像不支持vector建树?这样写会TLE,得用链式前向星进行优化,这样就不会TLE了,这里给出树状数组写法
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<stdio.h>
#include<cstdio>
#include<vector>
// #include<bits/stdc++.h>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
// #include<random>
#include<stack>
#include<string>
#define ll int
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
// mt19937 rnd(time(0));
const ll mod = 998244353;
const ll maxn = 1e5+5;
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
//vector<ll>g[100015];
ll cnt=0;
ll h[maxn];
ll ne[maxn<<1];
ll to[maxn<<1];
void ad(ll x,ll y)
{
to[cnt]=y;
ne[cnt]=h[x];
h[x]=cnt;
cnt++;
}
ll c1[maxn];
ll c2[maxn];
ll gs = 0;
pair<ll, ll>ans[maxn];
void dfs(ll k, ll fa)
{
gs++;
ll j=gs;
for(ll i=h[k];i>=0;i=ne[i])
{
if(to[i]==fa)continue;
dfs(to[i],k);
}
ans[k]={j,gs};
}
ll n;
void add(ll *t,ll x,ll v)
{
for(ll i=x;i<=n;i+=lowbit(i))
t[i]+=v;
return ;
}
ll ask(ll* t,ll x)
{
ll ans=0;
for(ll i=x;i>0;i-=lowbit(i))
{
ans+=t[i];
}
return ans;
}
ll q(ll l,ll r)
{
return r*ask(c1,r)-ask(c2,r)-((l-1)*ask(c1,l-1)-ask(c2,l-1));
}
inline ll read()
{
ll x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch>'9')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
return x * f;
}
int main()
{
//fio();
gs=0;
memset(h,-1,sizeof h);
n=read();
for(ll i=1;i<=n-1;i++)
{
ll l,r;
l=read();
r=read();
ad(l,r);
ad(r,l);
}
add(c1,1,1);
add(c2,1,0);
dfs(1,-1);
ll m;
m=read();
while(m--)
{
ll x;
char f[5];
scanf("%s",&f);
x=read();
if(f[0]=='Q')
{
printf("%d\n",q(ans[x].first,ans[x].second));
}
else
{
if(q(ans[x].first,ans[x].first)==1)
{
add(c1,ans[x].first,-1);
add(c1,ans[x].first+1,1);
add(c2,ans[x].first,(ans[x].first-1)*(-1));
add(c2,ans[x].first+1,ans[x].first*(1));
}
else
{
add(c1,ans[x].first,1);
add(c1,ans[x].first+1,-1);
add(c2,ans[x].first,(ans[x].first-1)*(1));
add(c2,ans[x].first+1,ans[x].first*(-1));
}
}
}
return 0;
}
华华和月月种树
https://ac.nowcoder.com/acm/problem/23051
题面:
华华看书了解到,一起玩养成类的游戏有助于两人培养感情。所以他决定和月月一起种一棵树。因为华华现在也是信息学高手了,所以他们种的树是信息学意义下的。
华华和月月一起维护了一棵动态有根树,每个点有一个权值。刚开存档的时候,树上只有0号节点,权值为0。接下来有两种操作:
操作1: 输入格式 \(1i\),表示月月氪金使节点 \(i\) 长出了一个新的儿子节点,权值为0,编号为当前最大编号+1(也可以理解为,当前是第几个操作 1,新节点的编号就是多少)。
操作2: 输入格式 \(2ia\),表示华华上线做任务使节点 \(i\) 的子树中所有节点(即它和它的所有子孙节点)权值加 \(a\)。
但是月月有时会检查华华有没有认真维护这棵树,会作出询问:
询问3: 输入格式 \(3i\),华华需要给出 \(i\) 节点此时的权值。
华华当然有认真种树了,不过还是希望能写个程序以备不时之需。
输入:
第一行一个正整数 \(M\),接下来 \(M\) 行,每行先输入一个正整数 \(O\) 表示操作类型,再输入一个非负整数 \(i\) 表示操作或询问的节点编号,如果 \(O=2\),再输入一个正整数 \(a\)。
输出:
对于每个询问 \(3\),输出一个非负整数表示询问的答案。
样例:
9
1 0
2 0 1
3 0
3 1
1 0
1 1
2 0 2
3 1
3 3
——————
1
1
3
2
数据范围:
\(1 \leq M \leq 4 \times 10^5\),保证操作1的数量不超过 \(10^5\),保证操作2中的参数 \(a\) 满足 \(1 \leq a \leq 999\)。
感受:感觉不难,但是错了快15次吧,为什么呢?一是手敲线段树,区间修改漏了每次都是修改区间值,二是认为可以二分要修改的范围,这里不是子树嵌套子树,所以二分不行。三是每次遇到新节点时,得减少值,这里直接问了区间和,然后区间里每个数减去区间和了。被自己逗笑了。思路就是离线+dfs序+线段树(区间修改+单点查询)
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
//#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
const ll maxn = 4e5 + 5;
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
struct s
{
ll v, l, r;
ll lazy;
}p[maxn << 2];
void build(ll i, ll l, ll r)
{
p[i].v = 0;
p[i].l = l, p[i].r = r;
p[i].lazy = 0;
if (l == r)
return;
build(i << 1, l, (l + r) >> 1);
build(i << 1 | 1, (l + r >> 1) + 1, r);
}
void push_down(ll i)
{
if (p[i].lazy)
{
p[i << 1].v += (p[i << 1].r - p[i << 1].l + 1) * p[i].lazy;
p[i << 1 | 1].v += (p[i << 1 | 1].r - p[i << 1 | 1].l + 1) * p[i].lazy;
p[i << 1 | 1].lazy += p[i].lazy;
p[i << 1].lazy += p[i].lazy;
p[i].lazy = 0;
}
}
void update(ll i, ll l, ll r, ll v)
{
if (l == p[i].l && r == p[i].r)
{
p[i].v += (r-l+1)*v;
p[i].lazy += v;
return;
}
push_down(i);
ll mid = (p[i].l + p[i].r) >> 1;
if (l <= mid)
update(i << 1, l, min(mid, r), v);
if (r >= mid + 1)
update(i << 1 | 1, max(mid + 1, l), r, v);
p[i].v = p[i << 1].v + p[i << 1 | 1].v;
}
ll query(ll i, ll l, ll r)
{
ll ans = 0;
if (l == p[i].l && r == p[i].r)
{
ans += p[i].v;
return ans;
}
push_down(i);
ll mid = (p[i].l + p[i].r) >> 1;
if (l <= mid)
ans += query(i << 1, l, min(mid, r));
if (r >= mid + 1)
ans += query(i << 1 | 1, max(mid + 1, l), r);
return ans;
}
vector<ll>g[500000];
ll a[maxn];
ll b[maxn << 1];
ll cnt = 0;
ll gs = 0;
void dfs(ll k, ll fa)
{
gs++;
b[gs] = k;
for (auto j : g[k])
{
dfs(j, k);
}
gs++;
b[gs] = k;
}
ll vis[maxn];
ll vi[maxn];
ll d[maxn];
pair<ll, ll>ans[maxn];
struct u
{
ll x;
ll l, r;
}f[maxn];
int main()
{
fio();
ll n;
cin >> n;
build(1, 1, n);
ll o = 1;
ll cs = 0;
for (ll i = 1; i <= n; i++)
{
cin >> f[i].x;
if (f[i].x == 2)cin >> f[i].l >> f[i].r;
else
{
cin >> f[i].l;
if (f[i].x == 1)
{
f[i].r=o;
g[f[i].l].push_back(o);
o++;
}
}
}
dfs(0, -1);
cnt = 0;
for (ll i = 1; i <= gs; i++)
{
if (vis[b[i]] == 0)
{
cnt++;
vis[b[i]] = cnt;
d[cnt] = vi[b[i]];
}
else
{
ans[b[i]] = { vis[b[i]],cnt };
}
}
cnt = 0;
ll fs=0;
for (ll i = 1; i <= n; i++)
{
if (f[i].x == 1)
{
ll u=query(1,ans[f[i].r].first,ans[f[i].r].first);
update(1, ans[f[i].r].first, ans[f[i].r].first, -u);
}
else if (f[i].x == 2)
{
update(1, ans[f[i].l].first, ans[f[i].l].second, f[i].r);
}
else if (f[i].x == 3)
{
cout << query(1, ans[f[i].l].first, ans[f[i].l].first) << endl;
}
}
}
A Growing Tree
https://codeforces.com/contest/1891/problem/F
题面:
你给定了一个根在顶点 \(1\) 的有根树,最初只包含一个顶点。每个顶点都有一个数值,初始设置为 \(0\)。还有 \(q\) 个查询,有两种类型:
-
第一种类型:向顶点 \(v\) 添加一个编号为 \(sz + 1\) 的子顶点,其中 \(sz\) 是树的当前大小。新顶点的数值将为 \(0\)。
-
第二种类型:将 \(x\) 加到顶点 \(v\) 的子树中所有顶点的数值上。
在所有查询完成后,输出最终树中所有顶点的数值。
输入:
第一行包含一个整数 \(T\)(\(1 \leq T \leq 10^4\))——测试用例的数量。测试用例的描述如下。
每个测试用例的第一行包含一个整数 \(q\)(\(1 \leq \leq 5 \cdot 10^5\))——查询的数量。
接下来的 \(q\) 行可以归为两种情况:
第一种类型的查询:第 \(i\) 行包含两个整数 \(t_i\)(\(t_i=1\)),\(v_i\)。你需要向顶点 \(v_i\) 添加一个编号为 \(sz+1\) 的子顶点,其中 \(sz\) 是树的当前大小。保证 \(1 \leq v_i \leq sz\)。
第二种类型的查询:第 \(i\) 2 行包含三个整数 \(t_i\)(\(t_i=2\)),\(v_i\),\(x_i\)(\(-10^9 \leq x_i \leq 10^9\))。你需要将 \(x_i\) 添加到 \(v_i\) 的子树中所有顶点的数值上。保证 \(1 \leq v_i \leq sz\),其中 \(sz\) 是树的当前大小。
保证所有测试用例中 \(q\) 的总和不超过 \(5 \cdot 10^5\)。
输出:
对于每个测试用例,在所有查询执行完毕后,输出最终树中每个顶点的数值。
样例:
3
9
2 1 3
1 1
2 2 1
1 1
2 3 2
1 3
2 1 4
1 3
2 3 2
5
2 1 1
1 1
2 1 -1
1 1
2 1 1
5
1 1
1 1
2 1 1
2 1 3
2 2 10
——————
7 5 8 6 2
1 0 1
4 14 4
感受:这个是上面的华华和月月种树弱化版,但是很奇怪我线段树开5e5+5的四倍空间竟然越界了,改成可5e5+10就过了,有点神奇。dfs序+线段树(区间修改+单点查询)
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
//#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
const ll maxn = 5e5 + 10;
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
struct s
{
ll v, l, r;
ll lazy;
}p[maxn << 2];
void build(ll i, ll l, ll r)
{
p[i].v = 0;
p[i].l = l, p[i].r = r;
p[i].lazy = 0;
if (l == r)
return;
build(i << 1, l, (l + r) >> 1);
build(i << 1 | 1, (l + r >> 1) + 1, r);
}
void push_down(ll i)
{
if (p[i].lazy)
{
p[i << 1].v += (p[i << 1].r - p[i << 1].l + 1) * p[i].lazy;
p[i << 1 | 1].v += (p[i << 1 | 1].r - p[i << 1 | 1].l + 1) * p[i].lazy;
p[i << 1 | 1].lazy += p[i].lazy;
p[i << 1].lazy += p[i].lazy;
p[i].lazy = 0;
}
}
void update(ll i, ll l, ll r, ll v)
{
if (l == p[i].l && r == p[i].r)
{
p[i].v += (r-l+1)*v;
p[i].lazy += v;
return;
}
push_down(i);
ll mid = (p[i].l + p[i].r) >> 1;
if (l <= mid)
update(i << 1, l, min(mid, r), v);
if (r >= mid + 1)
update(i << 1 | 1, max(mid + 1, l), r, v);
p[i].v = p[i << 1].v + p[i << 1 | 1].v;
}
ll query(ll i, ll l, ll r)
{
ll ans = 0;
if (l == p[i].l && r == p[i].r)
{
ans += p[i].v;
return ans;
}
push_down(i);
ll mid = (p[i].l + p[i].r) >> 1;
if (l <= mid)
ans += query(i << 1, l, min(mid, r));
if (r >= mid + 1)
ans += query(i << 1 | 1, max(mid + 1, l), r);
return ans;
}
vector<ll>g[500015];
ll b[maxn << 1];
ll cnt = 0;
ll gs = 0;
void dfs(ll k, ll fa)
{
gs++;
b[gs] = k;
for (auto j : g[k])
{
dfs(j, k);
}
gs++;
b[gs] = k;
}
ll vis[maxn];
pair<ll, ll>ans[maxn];
struct u
{
ll x;
ll l, r;
}f[maxn];
int main()
{
fio();
ll t;
cin>>t;
while(t--)
{
gs=0;
ll n;
cin >> n;
build(1, 1, n+5);
ll o = 2;
for (ll i = 1; i <= n; i++)
{
g[i].clear();
cin >> f[i].x;
if (f[i].x == 2)cin >> f[i].l >> f[i].r;
else
{
cin >> f[i].l;
f[i].r=o;
g[f[i].l].push_back(o);
o++;
}
}
dfs(1, -1);
cnt = 0;
for(ll i=1;i<=gs;i++)vis[b[i]]=0;
for (ll i = 1; i <= gs; i++)
{
if (vis[b[i]] == 0)
{
cnt++;
vis[b[i]] = cnt;
}
else
{
ans[b[i]] = { vis[b[i]],cnt };
}
}
cnt = 0;
ll fs=0;
for (ll i = 1; i <= n; i++)
{
if (f[i].x == 1)
{
ll u=query(1,ans[f[i].r].first,ans[f[i].r].first);
update(1, ans[f[i].r].first, ans[f[i].r].first, -u);
}
else if (f[i].x == 2)
{
update(1, ans[f[i].l].first, ans[f[i].l].second, f[i].r);
}
}
o--;
for(ll i=1;i<=o;i++)
{
cout<<query(1,ans[i].first,ans[i].first)<<" ";
}
cout<<endl;
}
}
Snacks
https://acm.hdu.edu.cn/showproblem.php?pid=5692
题面:
百度科技园内有n个零食机,零食机之间通过n−1条路相互连通。每个零食机都有一个值v,表示为小度熊提供零食的价值。
由于零食被频繁的消耗和补充,零食机的价值v会时常发生变化。小度熊只能从编号为0的零食机出发,并且每个零食机至多经过一次。另外,小度熊会对某个零食机的零食有所偏爱,要求路线上必须有那个零食机。
为小度熊规划一个路线,使得路线上的价值总和最大。
输入:
输入数据第一行是一个整数T(T≤10),表示有T组测试数据。
对于每组数据,包含两个整数n,m(1≤n,m≤100000),表示有n个零食机,m次操作。
接下来n−1行,每行两个整数x和y(0≤x,y<n),表示编号为x的零食机与编号为y的零食机相连。
接下来一行由n个数组成,表示从编号为0到编号为n−1的零食机的初始价值v(|v|<100000)。
接下来m行,有两种操作:0 x y,表示编号为x的零食机的价值变为y;1 x,表示询问从编号为0的零食机出发,必须经过编号为x零食机的路线中,价值总和的最大值。
本题可能栈溢出,辛苦同学们提交语言选择c++,并在代码的第一行加上:
#pragma comment(linker, "/STACK:1024000000,1024000000")
输出:
对于每组数据,首先输出一行”Case #?:”,在问号处应填入当前数据的组数,组数从1开始计算。
对于每次询问,输出从编号为0的零食机出发,必须经过编号为x零食机的路线中,价值总和的最大值。
样例:
1
6 5
0 1
1 2
0 3
3 4
5 3
7 -5 100 20 -5 -7
1 1
1 3
0 2 -1
1 1
1 5
————————
Case #1:
102
27
2
20
思路:我也是第一次做区间修改+最大值维护的,之前最多也就是单点修改+最大值维护。
但是如果对于线段树有理解的画,应该不会太难。每次加减值一定会把这个被修改的区间的最大值也会相应的加减值
离线+dfs序+线段树(区间修改+区间最大).我这里代码交G++才不会超时,C++会超时
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
const ll maxn = 100000 + 15;
struct s
{
ll l, r;
ll v1;
ll ad, v, cf;//ad为加法的懒惰标记,cf为乘法的懒惰标记
}p[maxn << 2];
void build(ll i, ll l, ll r)
{
p[i].l = l, p[i].r = r, p[i].v = 0;
p[i].ad = 0;
if (l == r)
{
return;
}
build(i << 1, l, (l + r) >> 1);
build(i << 1 | 1, ((l + r) >> 1) + 1, r);
}
void push_down(ll i)
{
if (p[i].ad)
{
p[i << 1].v += p[i].ad;
p[i << 1 | 1].v += p[i].ad;
p[i << 1].ad += p[i].ad;
p[i << 1 | 1].ad += p[i].ad;
p[i].v = max(p[i << 1].v, p[i << 1 | 1].v);
p[i].ad = 0;
}
}
void udq(ll i, ll ad, ll cf, ll l, ll r)//区间修改
{
if (p[i].l == l && p[i].r == r)
{
p[i].v += ad;
p[i].ad += ad;
return;
}
push_down(i);
ll i1 = i << 1, i2 = i << 1 | 1;
if (l <= p[i1].r)
{
udq(i1, ad, cf, l, min(p[i1].r, r));
}
if (r >= p[i2].l)
{
udq(i2, ad, cf, max(p[i2].l, l), r);
}
p[i].v = max(p[i << 1].v, p[i << 1 | 1].v);
}
ll query(ll i, ll l, ll r)
{
ll ans = LLONG_MIN;
if (p[i].l == l && p[i].r == r)
{
ans = p[i].v;
return ans;
}
push_down(i);
ll i1 = i << 1, i2 = i << 1 | 1;
ll l1,r1;
if (l <= p[i1].r)
{
ans = max(ans, query(i1, l, min(p[i1].r, r)));
}
if (r >= p[i2].l)
{
ans = max(ans, query(i2, max(l, p[i2].l), r));
}
p[i].v=max(p[i<<1].v,p[i<<1|1].v);
return ans;
}
inline ll read()
{
ll x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch>'9')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
return x * f;
}
vector<ll>g[200005];
ll gs = 0;
ll b[300005];
ll vis[200005];
ll a[200005];
pair<ll, ll>ans[200005];
void dfs(ll x, ll fa)
{
gs++;
ll k=gs;
for (auto j : g[x])
{
if (j == fa)continue;
dfs(j, x);
}
ans[x]={k,gs};
}
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
int main()
{
// fio();
ll t;
t = read();
for (ll io = 1; io <= t; io++)
{
gs = 0;
cout << "Case #" << io << ":" << endl;
ll n, m;
n = read();
m = read();
build(1, 1, n);
for (ll i = 0; i <= n; i++)g[i].clear(),vis[i] = 0;
for (ll i = 1; i <= n - 1; i++)
{
ll l, r;
l = read();
r = read();
g[l].push_back(r);
g[r].push_back(l);
}
ll cnt = 0;
dfs(0, -1);
for (ll i = 0; i <= n - 1; i++)
{
ll x;
x = read();
a[i] = x;
udq(1, x, 0, ans[i].first, ans[i].second);
}
while (m--)
{
ll op;
op = read();
if (op == 0)
{
ll x, y;
x = read();
y = read();
udq(1, y-a[x], 0, ans[x].first, ans[x].second);
a[x] = y;
}
else
{
ll x;
x = read();
cout << query(1, ans[x].first, ans[x].second) << endl;
}
}
}
}
Puzzled Elena
https://acm.hdu.edu.cn/showproblem.php?pid=5468
题面:
由于Stefan和Damon都爱上了Elena,而她很难做出选择。她的最好朋友Bonnie建议她向他们提出一个问题,然后她会根据谁能解决这个问题来做出选择。
假设有一棵树,有n个顶点和n-1条边,每个顶点都有一个值。根是顶点1。那么对于每个顶点,你能告诉我它的子树中有多少个顶点可以被认为是与它互质的吗?
注:如果两个顶点的值的最大公约数(GCD)等于1,则称这两个顶点是互质的
输入:
有多个测试(不超过8个)。
对于每个测试,第一行有一个数字n(1≤n≤105),之后有n-1行,每行有两个数字a和b(1≤a,b≤n),表示顶点a与顶点b相连。然后下一行有n个数字,第i个数字表示第i个顶点的值。顶点的值不低于1且不超过105。
输出:
对于每个测试,首先请输出“Case #k: ”,其中k是测试的编号。然后,请输出一行包含n个数字(用空格分隔),代表每个顶点的答案。
样例:
5
1 2
1 3
2 4
2 5
6 2 3 4 5
——————
Case #1: 1 1 0 0 0
感受:某个题集说是dfs序+容斥,感觉就是普通dfs+容斥。和dfs序运用联系不强。具体坐下来就感受到是根据dfs遍历下来的性质进行容斥而已。就是先预处理质因数的所有子集,具体容斥方法可以参考的上一篇博客的G题,然后正常dfs下来,进来先容斥一遍算互质的数的个数,回溯再再算一次容斥的数的个数。
两者相减即可,注意是多组输入。欧拉筛+容斥+dfs
https://www.cnblogs.com/cjcf/p/18551489
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<stdio.h>
#include<cstdio>
#include<vector>
// #include<bits/stdc++.h>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
// #include<random>
#include<stack>
#include<string>
#define ll int
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
// mt19937 rnd(time(0));
const ll mod = 998244353;
const ll maxn = 1e5+5;
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
ll h[120000];
ll ne[120000<<1];
ll to[100002<<1];
ll cnt=0;
ll a[120000];
bool vi[120000];
ll z[100002][100];
void add(ll l,ll r)
{
to[cnt]=r;
ne[cnt]=h[l];
h[l]=cnt++;
}
ll b[120000];
ll gs=0;
ll tj[120000];
ll cf=0;
ll shu[120000];
ll ut[100002];
ll rt[100002];
void dfs(ll x,ll fa)
{
ll gx=0;
for(ll i=1;i<=rt[x];i++)
{
if(ut[z[x][i]]%2)
gx+=tj[z[x][i]];
else
gx-=tj[z[x][i]];
tj[z[x][i]]++;
}
ll uo=cf-gx;//互质数
cf++;
for(ll i=h[x];i>=0;i=ne[i])
{
if(to[i]==fa)continue;
dfs(to[i],x);
}
gx=0;
ll op=0;
for(ll i=1;i<=rt[x];i++)
{
if(ut[z[x][i]]%2)
gx+=tj[z[x][i]];
else
gx-=tj[z[x][i]];
}
op=cf-gx;
shu[x]=op-uo;
}
bool st[120000];
void ola(ll x)
{
for(ll i=2;i<=x;i++)
{
if(!st[i])gs++,b[gs]=i,vi[b[gs]]=1;
for(ll j=1;b[j]<=x/i;j++)
{
st[b[j]*i]=1;
if(i%b[j]==0)break;
}
}
}
int main()
{
fio();
ll t;
ll n;
ll io=0;
ola(100000);
while(cin>>n)
{
io++;
cf=0;
cnt=0;
cout<<"Case #"<<io<<": ";
for(ll i=1;i<=n;i++)h[i]=-1;
for(ll i=1;i<=n-1;i++)
{
ll l,r;
cin>>l>>r;
add(l,r);
add(r,l);
}
ll d[150];
for(ll i=1;i<=n;i++)
{
cin>>a[i];
ll u=a[i];
ll fo=0;
for(ll k=1;k<=gs;k++)
{
if(u%b[k]==0)
{
while(u%b[k]==0)
{
u/=b[k];
}
fo++;
d[fo]=b[k];
}
if(u==1)
break;
if(vi[u])
{
fo++;
d[fo]=u;
break;
}
}
ll uo=0;
for(ll k=1;k<=(1ll<<fo)-1;k++)
{
ll co=0;
ll ans=1;
for(ll j=0;j<=fo-1;j++)
{
if((1ll<<j)&k)
{
co++;
ans*=d[j+1];
}
}
uo++;
z[i][uo]=ans;
ut[ans]=co;
}
rt[i]=uo;
}
dfs(1,-1);
for(ll i=1;i<=n;i++)
cout<<shu[i]<<" ";
cout<<endl;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号