牛客小白月赛104(A~D)
比赛链接:https://ac.nowcoder.com/acm/contest/94879#question
牛客还是经典暴力时要求代码贼多啊
A.小红购买装备
题目描述:
小红准备去打地下城,在进入地下城之前首先需要购买合适的装备。
已知商店共有\(n\)件装备,每种装备提供\(a_i\)的攻击和\(b_i\)的防御,价格为\(c_i\),小红身上已有的装备攻击为\(x\),防御为\(y\),该装备卖给商店可以回收\(z\)金币。另外小红拥有的金币数量为\(T\)。
小红的战斗力计算为攻击+防御。现在小红想知道自己最终从装备处可以获得的战斗力最大值是多少?
注:小红最多只能生效一件装备!
输入描述:
第一行输入五个正整数\(n, x, y, z, T\),分别代表商店的装备数量、小红身上的装备攻击、防御、回收价格,以及小红携带的金币。
接下来的\(n\)行,每行输入三个正整数,代表商店每件装备的攻击、防御和金币数量。
\(1 ≤ n ≤ 10^5\)
\(1 ≤ x, y, z, a_i, b_i, c_i, T ≤ 10^9\)
输出描述:
一个正整数,代表小红从装备处获得的最高战斗力。
输入:
2 100 30 50 100
120 50 120
200 100 1000
输出:
170
思路:小红最多只能生效一件装备!注意这句话,所以要么就是不换装备,要么就是把装备买掉,用总金额去买更好的
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
//#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
ll ksm(ll x, ll y)
{
ll ans = 1;
while (y)
{
if (y & 1)
{
ans = ans % mod * (x % mod) % mod;
}
x = x % mod * (x % mod) % mod;
y >>= 1;
}
return ans % mod % mod;
}
ll gcd(ll x, ll y)
{
if (y == 0)
return x;
else
return gcd(y, x % y);
}
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
int main()
{
fio();
ll n,x,y,z,t;
cin>>n>>x>>y>>z>>t;
ll ans=x+y;
ll op=x+y;
ll u=z+t;
for(ll i=1;i<=n;i++)
{
ll x,y,z;
cin>>x>>y>>z;
if(z<=u)
{
ans=max(ans,x+y);
}
}
cout<<ans<<endl;
}
B.小红招募英雄
小红将装备整备完毕,准备招募共同冒险的英雄。
已知英雄共有5种稀有度:N、R、SR、SSR、UR。小红每次招募将优先选择稀有度为SSR和UR的英雄。小红一共需要2名队友,现在给出每次招募出每个稀有度的概率,请你帮小红计算单次十连抽(等同于抽取10次)即可凑齐队友(即不小于2名SSR以上稀有度英雄)的概率。
输入描述:
五个小数p1, p2, p3, p4, p5,分别代表单次抽取时,N、R、SR、SSR、UR被抽到的概率。
\(0 ≤ p1, p2, p3, p4, p5 ≤ 1\)
\(p1 + p2 + p3 + p4 + p5 = 1\)
输出描述:
一个小数,代表小红单次十连抽即可凑齐两名队友的概率。如果相对误差或绝对误差不超过 \(10^-6\),您的答案将被接受。具体来说,设您的答案为 a,裁判的答案为 b,当且仅当 \(|a-b| ≤ max(1,|b|) * 10^{-6}\) 时,您的答案将被接受。
输入:
0.2 0.2 0.2 0.2 0.2
输出:
0.9536425984
思路:经典容斥,直接考虑不行的事件,即9次没有SSR和UR,和10次没有SSR和UR,最后用1减去这个概率
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
//#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
ll ksm(ll x, ll y)
{
ll ans = 1;
while (y)
{
if (y & 1)
{
ans = ans % mod * (x % mod) % mod;
}
x = x % mod * (x % mod) % mod;
y >>= 1;
}
return ans % mod % mod;
}
ll gcd(ll x, ll y)
{
if (y == 0)
return x;
else
return gcd(y, x % y);
}
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
int main()
{
fio();
double a[50];
double ans=0;
double u=0;
for(ll i=1;i<=5;i++)
{
cin>>a[i];
if(i<=3)
{
u+=a[i];
}
}
double cnt=1;
for(ll i=1;i<=10;i++)
{
cnt*=u;
if(i==9)
{
ans+=cnt*(a[4]+a[5])*10;
}
else if(i==10)
ans+=cnt;
}
ans=1-ans;
printf("%.10lf\n",ans);
}
C.小红打怪
有n个怪物排成一排,小红和队友们准备进攻这些怪物。
小红的技能是全体打击,对所有怪物造成1点伤害。
队友1的技能是单体打击,对单体怪物造成1点伤害。
队友2的技能是范围攻击,对相邻的两只怪物分别造成1点伤害(可以对死去的怪物尸体释放该技能)。
每回合每个人均可释放1次技能。小红想知道,击杀全部怪物最少需要多少回合?
输入描述:
第一行输入一个正整数n,代表怪物的总数。
第二行输入n个正整数\(a_i\),代表每个怪物的血量。
\(2 ≤ n ≤ 10^5\)
\(1 ≤ a_i ≤ 10^9\)
输出描述:
一个整数,代表击杀全部怪物的最少回合数。
输入:
5
1 2 3 4 5
输出:
2
思路:典型二分问题,这里用了优先队列,仔细想想其实直接遍历也行(自己搞复杂了)。直接二分可能的回合数,然后首先大家都减去回合数,剩下的数用优先队列开pair<ll,ll>,存数值和下标,每次询问头时,问下左边和右边有没有大于0的存在,有就进行第三种操作,无则进行第二种操作,如果不能进行第二种就进行第三种,否则反之,每次操作开始前记得比较下现在的头是否时正确的,否则弹出。最后如果两种操作都没有了,且队列还大于0,则返回0,否则返回1
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
ll ksm(ll x, ll y)
{
ll ans = 1;
while (y)
{
if (y & 1)
{
ans = ans % mod * (x % mod) % mod;
}
x = x % mod * (x % mod) % mod;
y >>= 1;
}
return ans % mod % mod;
}
ll gcd(ll x, ll y)
{
if (y == 0)
return x;
else
return gcd(y, x % y);
}
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
ll a[450000];
ll n;
ll b[450000];
ll ck(ll mid)
{
priority_queue<pair<ll,ll>>q;
for(ll i=1;i<=n;i++)
{
b[i]=a[i];
b[i]-=mid;
if(b[i]>0)
{
q.push({b[i],i});
}
}
b[n+1]=b[0]=0;
ll pd=1;
ll ans,cnt;
ans=cnt=mid;
while(!q.empty())
{
if(b[q.top().second]!=q.top().first)
{
q.pop();
continue;
}
if(q.top().first==0)
{
break;
}
if(ans==0&&cnt==0)
{
pd=0;
break;
}
if(ans>0)
{
ll x=q.top().first;
ll y=q.top().second;
q.pop();
ll z=ans;
if(b[y+1]>0)
{
z=min({z,b[y+1],b[y]});
b[y+1]-=z;
b[y]-=z;
ans-=z;
q.push({b[y+1],y+1});
q.push({b[y],y});
}
else if(b[y-1]>0)
{
z=min({z,b[y-1],b[y]});
b[y-1]-=z;
b[y]-=z;
ans-=z;
q.push({b[y-1],y-1});
q.push({b[y],y});
}
else
{
z=cnt;
if(cnt>0)
{
z=min({z,b[y]});
b[y]-=z;
cnt-=z;
q.push({b[y],y});
}
else
{
z=ans;
z=min(z,b[y]);
b[y]-=z;
ans-=z;
q.push({b[y],y});
}
}
}
else if(cnt>0)
{
ll x=q.top().first;
ll y=q.top().second;
q.pop();
ll z=cnt;
z=min(z,b[y]);
b[y]-=z;
cnt-=z;
q.push({b[y],y});
}
}
return pd;
}
int main()
{
fio();
cin>>n;
ll sum=0;
for(ll i=1;i<=n;i++)cin>>a[i],sum+=a[i];
ll l=1,r=(ll)1e9+5;
while(l<r)
{
ll mid=(l+r)>>1;
if(mid*n+mid+mid*2<sum)
{
l=mid+1;
continue;
}
if(ck(mid))
{
r=mid;
}
else
l=mid+1;
}
cout<<r<<endl;
}
D.小红开锁
小红来到了地下城的门口,发现门口有一个密码锁。
这个锁一共有n层,每层为一个正方形的图案。小红每次操作一次可以选择一层使其每个位置的元素按顺时针移动一个格子。
该图演示一个3层的锁,小红操作第二层时的变化。
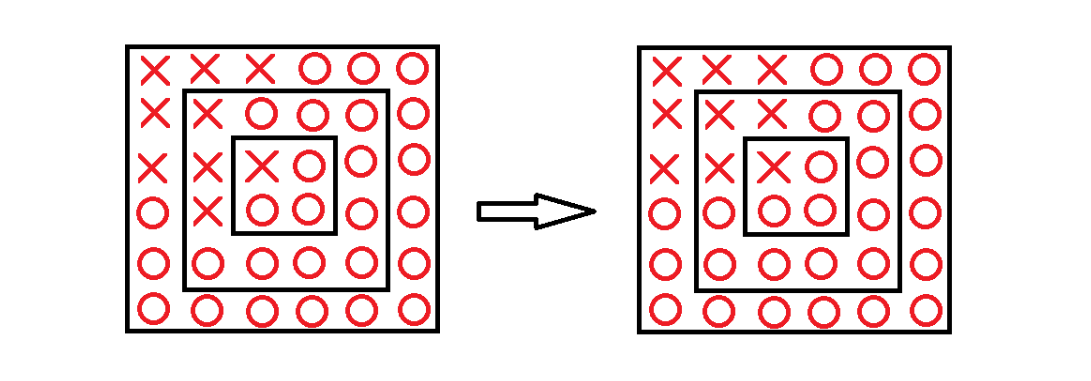
该锁以中心为原点建立平面直角坐标系后,每个象限为一个区域,共分为4个区域,当且仅当某个区域内全部为'X'图案、且其余三个区域全部为'O'图案时,锁被解开。
小红想知道,这个锁需要操作最少多少次可以解开?
输入描述:
第一行输入一个正整数n,代表锁的层数。
接下来输入2n行,每行输入一个长度为2n的字符串,用来表示锁的初始图案。
1 ≤ n ≤ 100
保证存在一个合法的开锁方式。
输出描述:
一个整数,代表小红需要操作的最少次数。
输入:
2
OXXX
OOOO
OXOO
OOOO
输出:
3
思路:暴力就行了,讨论四个角,这里给出一个优化暴力的方法,从左上角顺时针一个圈标记一个位置如1 2 3 等等,最终长度可以根据边长来进行计算。然后每次也是从左上角走一个顺时针圈,遇到X标记一下,如果X断开就说明现在是X段的头,然后讨论下它的位置和我要去的标记点的位置就可以了,这里写个函数,十分方便四个后续三个角讨论(这四个标记位置可由观察规律得出),最终四个方案下取个最优的就行了。具体推荐看看代码
#include<iostream>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<deque>
#include<cctype>
#include<string.h>
#include<math.h>
#include<time.h>
#include<random>
#include<stack>
#include<string>
#define ll long long
#define lowbit(x) (x & -x)
#define endl "\n"// 交互题记得删除
using namespace std;
mt19937 rnd(time(0));
const ll mod = 998244353;
ll ksm(ll x, ll y)
{
ll ans = 1;
while (y)
{
if (y & 1)
{
ans = ans % mod * (x % mod) % mod;
}
x = x % mod * (x % mod) % mod;
y >>= 1;
}
return ans % mod % mod;
}
ll gcd(ll x, ll y)
{
if (y == 0)
return x;
else
return gcd(y, x % y);
}
void fio()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
}
string f[25000];
ll ck(ll v,ll l,ll r,ll z,ll y,ll cd)
{
ll pd=0;
ll wz=0;
for(ll i=z;i<=y;i++)
{
if(pd==-1)
break;
if(pd==0)
{
wz++;
if(f[l][i]=='X')
pd=1;
}
else
{
wz++;
if(f[l][i]=='O')
{
wz--;
pd=-1;
break;
}
}
}
for(ll i=l+1;i<=r;i++)
{
if(pd==-1)
break;
if(pd==0)
{
wz++;
if(f[i][y]=='X')
pd=1;
}
else
{
wz++;
if(f[i][y]=='O')
{
wz--;
pd=-1;
break;
}
}
}
for(ll i=y-1;i>=z;i--)
{
if(pd==-1)
break;
if(pd==0)
{
wz++;
if( f[r][i]=='X')
pd=1;
}
else
{
wz++;
if(f[r][i]=='O')
{
wz--;
pd=-1;
break;
}
}
}
for(ll i=r-1;i>=l+1;i--)
{
if(pd==-1)
break;
if(pd==0)
{
wz++;
if(f[i][z]=='X')
pd=1;
}
else
{
wz++;
if(f[i][z]=='O')
{
wz--;
pd=-1;
break;
}
}
}
if(wz<=v)
{
return v-wz;
}
else
{
return cd-wz+v;
}
}
int main()
{
fio();
ll n;
cin>>n;
for(ll i=1;i<=2*n;i++)
{
cin>>f[i];
f[i]='0'+f[i];
}
//左上
ll l=1,r=2*n,z=1,y=2*n;
ll ans=999999999999999;
ll cnt=0;
for(ll i=1;i<=n;i++)
{
ll cd=(n-i+1)*2;
cd=cd+cd-1+cd-1+cd-2;
cnt+=ck(n-i+1,l,r,z,y,cd);
l++;
r--;
z++;
y--;
}
ans=min(ans,cnt);
// 左下
cnt=0;
l=1,r=2*n,z=1,y=2*n;
for(ll i=1;i<=n;i++)
{
ll cd=(n-i+1)*2;
ll k=cd+cd-1+cd-1+(n-i);
cd=cd+cd-1+cd-1+cd-2;
cnt+=ck(k,l,r,z,y,cd);
l++;
r--;
z++;
y--;
}
ans=min(ans,cnt);
//右上
cnt=0;
l=1,r=2*n,z=1,y=2*n;
for(ll i=1;i<=n;i++)
{
ll cd=(n-i+1)*2; ll k=cd+(n-i);
cd=cd+cd-1+cd-1+cd-2;
cnt+=ck(k,l,r,z,y,cd);
l++;
r--;
z++;
y--;
}
ans=min(ans,cnt);
cnt=0;
l=1,r=2*n,z=1,y=2*n;
for(ll i=1;i<=n;i++)
{
ll cd=(n-i+1)*2; ll k=cd+cd-1+n-i;
cd=cd+cd-1+cd-1+cd-2;
cnt+=ck(k,l,r,z,y,cd);
l++;
r--;
z++;
y--;
}
ans=min(ans,cnt);
cout<<ans<<endl;
}
E.小红开宝箱
思路:赛时不会做,赛后看了思路,是一个树的图论,基环树+拓扑,基环树我是真不晓得,涉及过浅,后几天再补上


 浙公网安备 33010602011771号
浙公网安备 33010602011771号