生成模型
AE
VAE
GAN
应用目标
生成式任务(生成、重建、超分辨率、风格迁移、补全、上采样等)
核心思想
生成器G和判别器D的一代代博弈
- 生成器G:生成网络,通过输入生成图像,希望生成的数据可以让D分辨不出来
- 判别器D:二分类网络,将生成器生成图像作为负样本,真实图像作为正样本,希望尽可能分辨出G生成的数据和真实数据的分布
- 判别器D训练:给定G,通过G生成图像产生负样本,并结合真实图像作为正样本来训练D
- 生成器G训练:给定D,以使得D对G生成图像的评分尽可能接近正样本作为目标来训练G
- G和D的训练过程交替进行,对抗过程使得G生成的图像越来越逼真,D分辨真假的能力越来越强
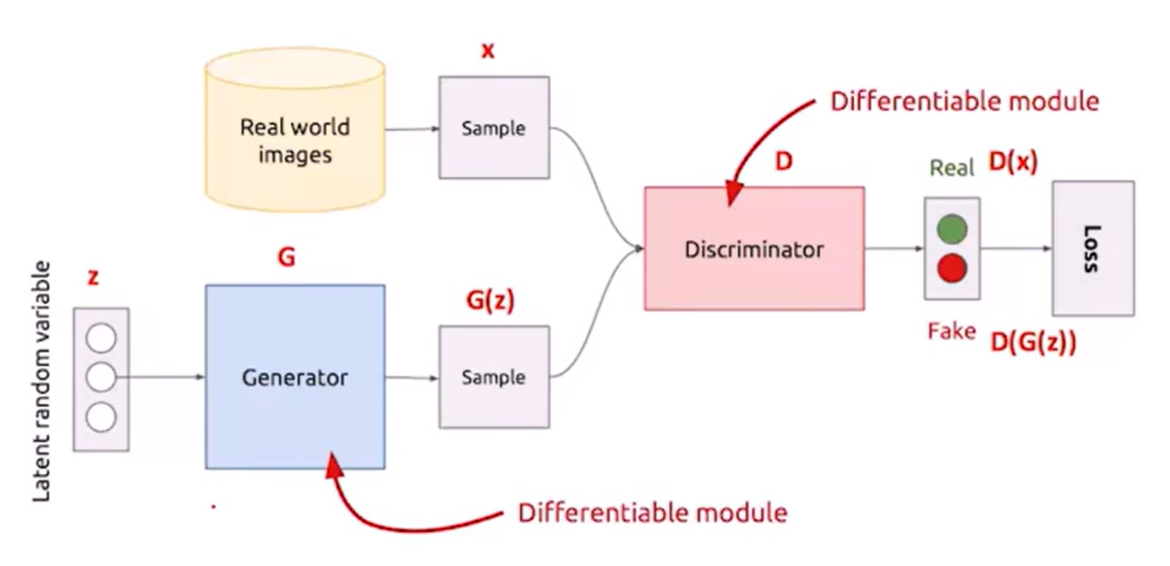
算法原理
GAN的精妙之处:对生成模型损失函数的处理
G(生成网络):接受一个随机噪声\(z\),通过该噪声生成图片,记作\(G(z)\)
输入噪声的随机性可以带来生成图像的多样性
D(判别网络):输入参数为\(x\),\(x\)代表一张图片,输出\(D(x)\)代表\(x\)为真实图片的概率,如果为1,就代表100%是真实图片,若为0,则代表不可能是真实的图片
问题分析
目标函数如何分析?

对数函数:在其定义域内是单调递增函数,数据取对数不改变数据间的相对关系,使用\(log\)后,可放大损失,便于计算和优化
-
前半部分公式 $$E_{x\backsim p_{data}(x)}[logD(x)]$$
- \(D(x)\)表示判别器对真实图片的判别,取对数函数后目的是为了其值趋于0,也就是\(D(x)\)趋于1,也就是放大损失
- \(E_{x\backsim p_{data}(x)}\)表示期望\(x\)从\(p_{data}\)中获取
- \(x\)表示真实的数据(图片)
- \(P_{data}\)表示真实数据的分布
- 综上所述,前半部分公式
- 含义:判别器判别出真实数据的概率。
- 优化目标:使得该概率越大越好
-
后半部分公式 $$E_{z\backsim p_{z}(z)}[log(1-D(G(z)))] $$
- \(E_{z\backsim p_{z}(z)}\)表示期望\(z\)从\(p_{z}\)中获取
- \(z\)表示随机的噪声
- \(P_{z}(z)\)表示生成随机噪声的分布
- 对于判别器D来说,若输入的是生成数据(\(D(G(z))\)),其目标便是将生成数据判定为0(即\(D(G(z))=0\)),也就是希望\(log(1-D(G(z)))\)越大越好
- 对于生成器G来说,其目的是生成的数据被判别器识别为真(即\(D(G(z))=1\)),也就是希望\(log(1-D(G(z)))\)越小越好
- 综上所述,D和G的优化目标相反
- \(E_{z\backsim p_{z}(z)}\)表示期望\(z\)从\(p_{z}\)中获取
-
总结
- 对于判别器D,最大化\(logD(x)\)和\(log(1-D(G(z)))\),从而达到最大化\(V(D,G)\)
- 对于生成器G,最小化\(log(1-D(G(z)))\),从而达到最小化\(V(D,G)\) 的目标
先更新D参数指导G方向
公式解析:$$min_{G}max_{D}V(D,G)=E_{x\backsim p_{data}(x)}[logD(x)]+E_{z\backsim p_{z}(z)}[log(1-D(G(z)))] $$
- 先算 \(max_{D}V(D,G)=E_{x\backsim p_{data}(x)}[logD(x)]+E_{z\backsim p_{z}(z)}[log(1-D(G(z)))]\),固定G,用D区分正负样本,因此是\(max_{D}\)
- 后算 整体 ,判别式D固定不动,通过调整生成器G,希望判别器不失误,尽可能不让判别器区分出正负样本(提高生成图像的真实性)
每训练出一个生成器,就要生出一个判别器,判别器要使真实图像的值尽可能的大,生成图像的值尽可能的小。也就是说让判别器具有更强的判别能力。是个动态的问题,跟以前损失函数恒定不变的思想不同
如何生成图片?
G和D应该如何设置?
如何进行训练?
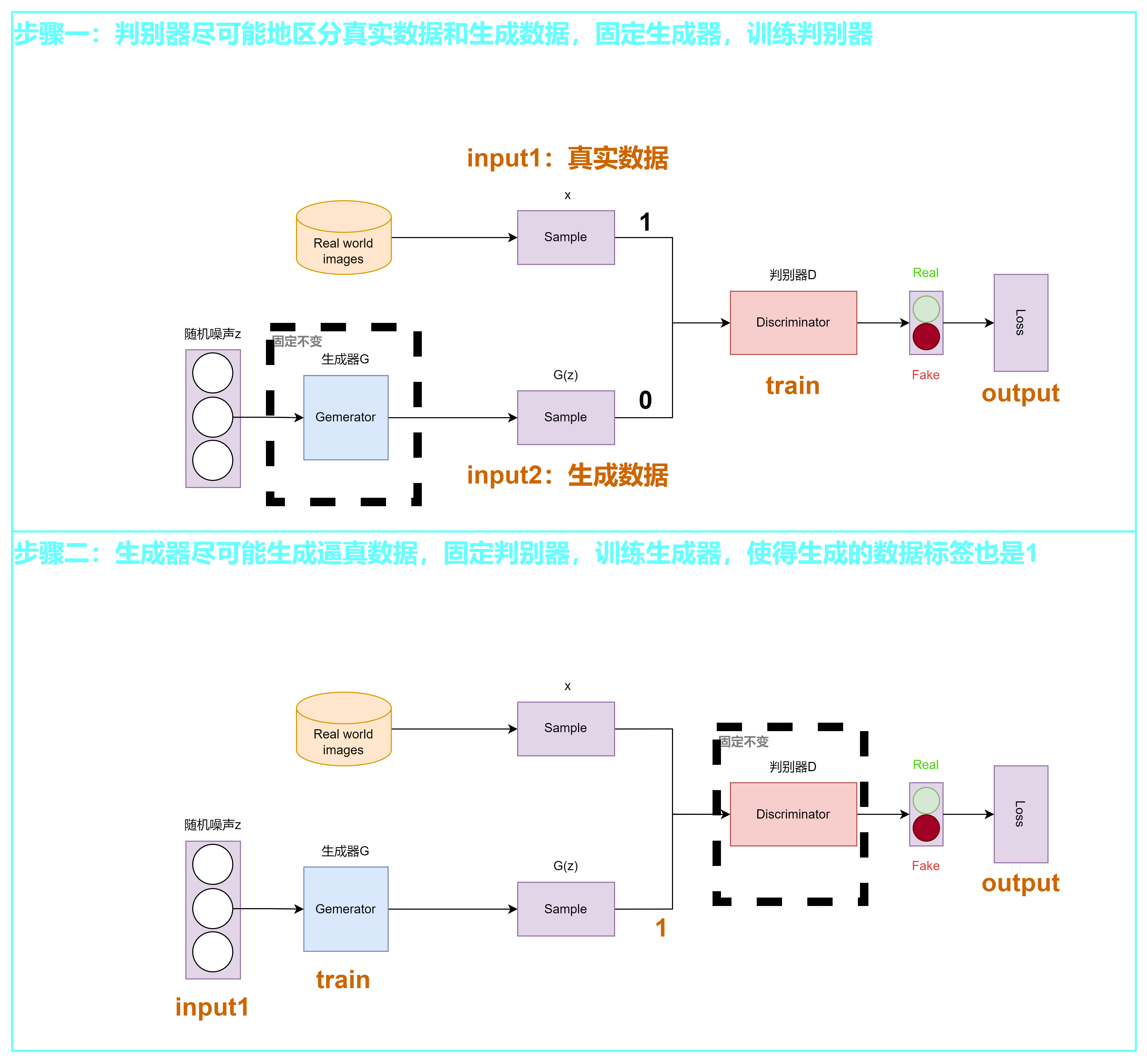
点击查看代码
for 迭代 in range(迭代总数):
for batch in range(batch_size):
新batch = input1的batch + input2的batch # (batch加倍)
for 轮数 in range(判别器总轮数):
步骤一
步骤二
损失函数
生成器损失(能否生成近似真实图片并使得判别器将生成图片判定为真):通过判别器的输出来计算
判别器损失(能否正确区分生成的图片和真实图片):判别器输出为一个概率值,通过交叉熵计算
代码实现
加载数据集(并可视化)
import numpy as np
import torch
import matplotlib.pyplot as plt
from torchvision import datasets
import torchvision.transforms as transforms
# number of subprocesses to use for data loading
num_workers = 0
# how many samples per batch to load
batch_size = 64
# convert data to torch.FloatTensor
transform = transforms.ToTensor()
# get the training datasets
train_data = datasets.MNIST(root='data', train=True,
download=True, transform=transform)
# prepare data loader
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
num_workers=num_workers)
# 可视化
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy()
# get one image from the batch
img = np.squeeze(images[0])
fig = plt.figure(figsize = (3,3))
ax = fig.add_subplot(111)
ax.imshow(img, cmap='gray')
import torch.nn as nn
import torch.nn.functional as F
class Discriminator(nn.Module):
def __init__(self, input_size, hidden_dim, output_size):
super(Discriminator, self).__init__()
# define hidden linear layers
self.fc1 = nn.Linear(input_size, hidden_dim*4)
self.fc2 = nn.Linear(hidden_dim*4, hidden_dim*2)
self.fc3 = nn.Linear(hidden_dim*2, hidden_dim)
# final fully-connected layer
self.fc4 = nn.Linear(hidden_dim, output_size)
# dropout layer
self.dropout = nn.Dropout(0.3)
def forward(self, x):
# flatten image
x = x.view(-1, 28*28)
# all hidden layers
x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc2(x), 0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc3(x), 0.2)
x = self.dropout(x)
# final layer
out = self.fc4(x)
return out
class Generator(nn.Module):
def __init__(self, input_size, hidden_dim, output_size):
super(Generator, self).__init__()
# define hidden linear layers
self.fc1 = nn.Linear(input_size, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, hidden_dim*2)
self.fc3 = nn.Linear(hidden_dim*2, hidden_dim*4)
# final fully-connected layer
self.fc4 = nn.Linear(hidden_dim*4, output_size)
# dropout layer
self.dropout = nn.Dropout(0.3)
def forward(self, x):
# all hidden layers
x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc2(x), 0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc3(x), 0.2)
x = self.dropout(x)
# final layer with tanh applied
out = F.tanh(self.fc4(x))
return out
# Discriminator hyperparams
# Size of input image to discriminator (28*28)
input_size = 784
# Size of discriminator output (real or fake)
d_output_size = 1
# Size of last hidden layer in the discriminator
d_hidden_size = 32
# Generator hyperparams
# Size of latent vector to give to generator
z_size = 100
# Size of discriminator output (generated image)
g_output_size = 784
# Size of first hidden layer in the generator
g_hidden_size = 32
# instantiate discriminator and generator
D = Discriminator(input_size, d_hidden_size, d_output_size)
G = Generator(z_size, g_hidden_size, g_output_size)
# check that they are as you expect
print(D)
print()
print(G)
Discriminator(
(fc1): Linear(in_features=784, out_features=128, bias=True)
(fc2): Linear(in_features=128, out_features=64, bias=True)
(fc3): Linear(in_features=64, out_features=32, bias=True)
(fc4): Linear(in_features=32, out_features=1, bias=True)
(dropout): Dropout(p=0.3)
)
Generator(
(fc1): Linear(in_features=100, out_features=32, bias=True)
(fc2): Linear(in_features=32, out_features=64, bias=True)
(fc3): Linear(in_features=64, out_features=128, bias=True)
(fc4): Linear(in_features=128, out_features=784, bias=True)
(dropout): Dropout(p=0.3)
)
# Calculate losses
def real_loss(D_out, smooth=False):
batch_size = D_out.size(0)
# label smoothing
if smooth:
# smooth, real labels = 0.9
labels = torch.ones(batch_size)*0.9
else:
labels = torch.ones(batch_size) # real labels = 1
# numerically stable loss
criterion = nn.BCEWithLogitsLoss()
# calculate loss
loss = criterion(D_out.squeeze(), labels)
return loss
def fake_loss(D_out):
batch_size = D_out.size(0)
labels = torch.zeros(batch_size) # fake labels = 0
criterion = nn.BCEWithLogitsLoss()
# calculate loss
loss = criterion(D_out.squeeze(), labels)
return loss
import torch.optim as optim
# Optimizers
lr = 0.002
# Create optimizers for the discriminator and generator
d_optimizer = optim.Adam(D.parameters(), lr)
g_optimizer = optim.Adam(G.parameters(), lr)
import pickle as pkl
# training hyperparams
num_epochs = 100
# keep track of loss and generated, "fake" samples
samples = []
losses = []
print_every = 400
# Get some fixed data for sampling. These are images that are held
# constant throughout training, and allow us to inspect the model's performance
sample_size=16
fixed_z = np.random.uniform(-1, 1, size=(sample_size, z_size))
fixed_z = torch.from_numpy(fixed_z).float()
# train the network
D.train()
G.train()
for epoch in range(num_epochs):
for batch_i, (real_images, _) in enumerate(train_loader):
batch_size = real_images.size(0)
## Important rescaling step ##
real_images = real_images*2 - 1 # rescale input images from [0,1) to [-1, 1)
# ============================================
# TRAIN THE DISCRIMINATOR
# ============================================
d_optimizer.zero_grad()
# 1. Train with real images
# Compute the discriminator losses on real images
# smooth the real labels
D_real = D(real_images)
d_real_loss = real_loss(D_real, smooth=True)
# 2. Train with fake images
# Generate fake images
z = np.random.uniform(-1, 1, size=(batch_size, z_size))
z = torch.from_numpy(z).float()
fake_images = G(z)
# Compute the discriminator losses on fake images
D_fake = D(fake_images)
d_fake_loss = fake_loss(D_fake)
# add up loss and perform backprop
d_loss = d_real_loss + d_fake_loss
d_loss.backward()
d_optimizer.step()
# =========================================
# TRAIN THE GENERATOR
# =========================================
g_optimizer.zero_grad()
# 1. Train with fake images and flipped labels
# Generate fake images
z = np.random.uniform(-1, 1, size=(batch_size, z_size))
z = torch.from_numpy(z).float()
fake_images = G(z)
# Compute the discriminator losses on fake images
# using flipped labels!
D_fake = D(fake_images)
g_loss = real_loss(D_fake) # use real loss to flip labels
# perform backprop
g_loss.backward()
g_optimizer.step()
# Print some loss stats
if batch_i % print_every == 0:
# print discriminator and generator loss
print('Epoch [{:5d}/{:5d}] | d_loss: {:6.4f} | g_loss: {:6.4f}'.format(
epoch+1, num_epochs, d_loss.item(), g_loss.item()))
## AFTER EACH EPOCH##
# append discriminator loss and generator loss
losses.append((d_loss.item(), g_loss.item()))
# generate and save sample, fake images
G.eval() # eval mode for generating samples
samples_z = G(fixed_z)
samples.append(samples_z)
G.train() # back to train mode
# Save training generator samples
with open('train_samples.pkl', 'wb') as f:
pkl.dump(samples, f)
训练损失如下:
Epoch [ 1/ 100] | d_loss: 1.4183 | g_loss: 0.6135
Epoch [ 1/ 100] | d_loss: 0.9797 | g_loss: 3.5072
Epoch [ 1/ 100] | d_loss: 0.6198 | g_loss: 5.3375
Epoch [ 2/ 100] | d_loss: 9.4996 | g_loss: 0.4747
Epoch [ 2/ 100] | d_loss: 1.0309 | g_loss: 2.0515
Epoch [ 2/ 100] | d_loss: 0.9327 | g_loss: 1.7079
Epoch [ 3/ 100] | d_loss: 2.1240 | g_loss: 1.3280
Epoch [ 3/ 100] | d_loss: 0.9323 | g_loss: 1.2268
Epoch [ 3/ 100] | d_loss: 1.1284 | g_loss: 1.5946
Epoch [ 4/ 100] | d_loss: 2.1666 | g_loss: 3.2032
Epoch [ 4/ 100] | d_loss: 0.7609 | g_loss: 1.6455
Epoch [ 4/ 100] | d_loss: 0.9046 | g_loss: 3.0293
Epoch [ 5/ 100] | d_loss: 1.7139 | g_loss: 1.2261
Epoch [ 5/ 100] | d_loss: 0.7299 | g_loss: 10.3912
Epoch [ 5/ 100] | d_loss: 0.3566 | g_loss: 27.5909
Epoch [ 6/ 100] | d_loss: 6.6589 | g_loss: 6.5818
Epoch [ 6/ 100] | d_loss: 0.4291 | g_loss: 14.8082
Epoch [ 6/ 100] | d_loss: 0.3489 | g_loss: 17.6337
Epoch [ 7/ 100] | d_loss: 3.3547 | g_loss: 9.0117
Epoch [ 7/ 100] | d_loss: 0.3846 | g_loss: 19.2056
Epoch [ 7/ 100] | d_loss: 0.3466 | g_loss: 17.6365
Epoch [ 8/ 100] | d_loss: 0.3601 | g_loss: 17.7147
Epoch [ 8/ 100] | d_loss: 0.4702 | g_loss: 26.0832
Epoch [ 8/ 100] | d_loss: 0.3763 | g_loss: 20.9755
Epoch [ 9/ 100] | d_loss: 0.6864 | g_loss: 11.5328
Epoch [ 9/ 100] | d_loss: 0.4102 | g_loss: 15.1188
Epoch [ 9/ 100] | d_loss: 0.3541 | g_loss: 18.3997
Epoch [ 10/ 100] | d_loss: 0.6527 | g_loss: 13.2949
Epoch [ 10/ 100] | d_loss: 0.4098 | g_loss: 12.7677
Epoch [ 10/ 100] | d_loss: 0.4056 | g_loss: 14.1539
Epoch [ 11/ 100] | d_loss: 0.9110 | g_loss: 18.9935
Epoch [ 11/ 100] | d_loss: 0.3591 | g_loss: 11.9452
Epoch [ 11/ 100] | d_loss: 0.3530 | g_loss: 19.7258
Epoch [ 12/ 100] | d_loss: 2.2365 | g_loss: 12.2991
Epoch [ 12/ 100] | d_loss: 0.3457 | g_loss: 17.7986
Epoch [ 12/ 100] | d_loss: 0.3648 | g_loss: 19.3954
Epoch [ 13/ 100] | d_loss: 2.0952 | g_loss: 12.1697
Epoch [ 13/ 100] | d_loss: 0.3805 | g_loss: 9.8293
Epoch [ 13/ 100] | d_loss: 0.3445 | g_loss: 20.9563
Epoch [ 14/ 100] | d_loss: 0.8317 | g_loss: 17.5827
Epoch [ 14/ 100] | d_loss: 0.3667 | g_loss: 16.4045
Epoch [ 14/ 100] | d_loss: 0.3387 | g_loss: 18.5352
Epoch [ 15/ 100] | d_loss: 0.7394 | g_loss: 16.3790
Epoch [ 15/ 100] | d_loss: 0.3785 | g_loss: 12.4679
Epoch [ 15/ 100] | d_loss: 0.3351 | g_loss: 21.7534
Epoch [ 16/ 100] | d_loss: 1.0355 | g_loss: 15.6396
Epoch [ 16/ 100] | d_loss: 0.3729 | g_loss: 7.6380
Epoch [ 16/ 100] | d_loss: 0.3675 | g_loss: 15.9038
Epoch [ 17/ 100] | d_loss: 0.8700 | g_loss: 12.5654
Epoch [ 17/ 100] | d_loss: 0.4025 | g_loss: 9.8733
Epoch [ 17/ 100] | d_loss: 0.3840 | g_loss: 16.0042
Epoch [ 18/ 100] | d_loss: 0.7950 | g_loss: 13.7673
Epoch [ 18/ 100] | d_loss: 0.3454 | g_loss: 11.1624
Epoch [ 18/ 100] | d_loss: 0.3722 | g_loss: 14.9801
Epoch [ 19/ 100] | d_loss: 0.4957 | g_loss: 13.4140
Epoch [ 19/ 100] | d_loss: 0.3782 | g_loss: 10.0773
Epoch [ 19/ 100] | d_loss: 0.3422 | g_loss: 18.9227
Epoch [ 20/ 100] | d_loss: 0.3525 | g_loss: 15.9695
Epoch [ 20/ 100] | d_loss: 0.3397 | g_loss: 12.6761
Epoch [ 20/ 100] | d_loss: 0.3352 | g_loss: 18.0243
Epoch [ 21/ 100] | d_loss: 0.9658 | g_loss: 14.0450
Epoch [ 21/ 100] | d_loss: 0.3488 | g_loss: 12.1490
Epoch [ 21/ 100] | d_loss: 0.3339 | g_loss: 17.1810
Epoch [ 22/ 100] | d_loss: 0.6433 | g_loss: 14.0821
Epoch [ 22/ 100] | d_loss: 0.3382 | g_loss: 16.5094
Epoch [ 22/ 100] | d_loss: 0.3544 | g_loss: 19.1663
Epoch [ 23/ 100] | d_loss: 1.5242 | g_loss: 10.9259
Epoch [ 23/ 100] | d_loss: 0.3641 | g_loss: 14.2070
Epoch [ 23/ 100] | d_loss: 0.3361 | g_loss: 19.6924
Epoch [ 24/ 100] | d_loss: 0.8881 | g_loss: 16.3108
Epoch [ 24/ 100] | d_loss: 0.4295 | g_loss: 10.7050
Epoch [ 24/ 100] | d_loss: 0.3383 | g_loss: 15.5534
Epoch [ 25/ 100] | d_loss: 0.4760 | g_loss: 16.3258
Epoch [ 25/ 100] | d_loss: 0.3646 | g_loss: 11.3346
Epoch [ 25/ 100] | d_loss: 0.3497 | g_loss: 17.2252
Epoch [ 26/ 100] | d_loss: 0.4799 | g_loss: 18.8594
Epoch [ 26/ 100] | d_loss: 0.3793 | g_loss: 10.4789
Epoch [ 26/ 100] | d_loss: 0.3610 | g_loss: 18.0723
Epoch [ 27/ 100] | d_loss: 0.5806 | g_loss: 16.5386
Epoch [ 27/ 100] | d_loss: 0.4071 | g_loss: 11.2509
Epoch [ 27/ 100] | d_loss: 0.3344 | g_loss: 19.1435
Epoch [ 28/ 100] | d_loss: 0.7388 | g_loss: 15.6390
Epoch [ 28/ 100] | d_loss: 0.3862 | g_loss: 10.3167
Epoch [ 28/ 100] | d_loss: 0.3493 | g_loss: 21.1869
Epoch [ 29/ 100] | d_loss: 1.6755 | g_loss: 10.4002
Epoch [ 29/ 100] | d_loss: 0.3782 | g_loss: 9.7869
Epoch [ 29/ 100] | d_loss: 0.3460 | g_loss: 17.8775
Epoch [ 30/ 100] | d_loss: 0.8180 | g_loss: 11.2492
Epoch [ 30/ 100] | d_loss: 0.4636 | g_loss: 7.5997
Epoch [ 30/ 100] | d_loss: 0.3632 | g_loss: 15.7323
Epoch [ 31/ 100] | d_loss: 0.6391 | g_loss: 15.8171
Epoch [ 31/ 100] | d_loss: 0.3859 | g_loss: 12.1420
Epoch [ 31/ 100] | d_loss: 0.3341 | g_loss: 11.3105
Epoch [ 32/ 100] | d_loss: 0.6047 | g_loss: 13.8931
Epoch [ 32/ 100] | d_loss: 0.4110 | g_loss: 9.5100
Epoch [ 32/ 100] | d_loss: 0.3708 | g_loss: 15.7434
Epoch [ 33/ 100] | d_loss: 0.7056 | g_loss: 13.9771
Epoch [ 33/ 100] | d_loss: 0.4062 | g_loss: 11.1046
Epoch [ 33/ 100] | d_loss: 0.3318 | g_loss: 14.1029
Epoch [ 34/ 100] | d_loss: 1.2167 | g_loss: 11.7245
Epoch [ 34/ 100] | d_loss: 0.4461 | g_loss: 7.3524
Epoch [ 34/ 100] | d_loss: 0.3491 | g_loss: 13.6828
Epoch [ 35/ 100] | d_loss: 1.0649 | g_loss: 11.6849
Epoch [ 35/ 100] | d_loss: 0.4522 | g_loss: 8.2442
Epoch [ 35/ 100] | d_loss: 0.3453 | g_loss: 15.2782
Epoch [ 36/ 100] | d_loss: 1.7150 | g_loss: 10.2848
Epoch [ 36/ 100] | d_loss: 0.4152 | g_loss: 7.9770
Epoch [ 36/ 100] | d_loss: 0.3413 | g_loss: 15.9781
Epoch [ 37/ 100] | d_loss: 1.4314 | g_loss: 13.1972
Epoch [ 37/ 100] | d_loss: 0.4598 | g_loss: 9.6094
Epoch [ 37/ 100] | d_loss: 0.3980 | g_loss: 15.6485
Epoch [ 38/ 100] | d_loss: 1.4494 | g_loss: 11.0654
Epoch [ 38/ 100] | d_loss: 0.4490 | g_loss: 9.5278
Epoch [ 38/ 100] | d_loss: 0.3500 | g_loss: 14.6877
Epoch [ 39/ 100] | d_loss: 1.5234 | g_loss: 13.8237
Epoch [ 39/ 100] | d_loss: 0.3995 | g_loss: 11.1140
Epoch [ 39/ 100] | d_loss: 0.4001 | g_loss: 14.4916
Epoch [ 40/ 100] | d_loss: 2.0880 | g_loss: 9.9507
Epoch [ 40/ 100] | d_loss: 0.4193 | g_loss: 10.2406
Epoch [ 40/ 100] | d_loss: 0.3678 | g_loss: 14.5487
Epoch [ 41/ 100] | d_loss: 2.2361 | g_loss: 10.1447
Epoch [ 41/ 100] | d_loss: 0.3992 | g_loss: 11.9671
Epoch [ 41/ 100] | d_loss: 0.4041 | g_loss: 18.2163
Epoch [ 42/ 100] | d_loss: 1.5434 | g_loss: 10.6550
Epoch [ 42/ 100] | d_loss: 0.4292 | g_loss: 8.3420
Epoch [ 42/ 100] | d_loss: 0.3707 | g_loss: 17.8904
Epoch [ 43/ 100] | d_loss: 1.4780 | g_loss: 14.2423
Epoch [ 43/ 100] | d_loss: 0.4213 | g_loss: 15.0119
Epoch [ 43/ 100] | d_loss: 0.3488 | g_loss: 14.9278
Epoch [ 44/ 100] | d_loss: 1.3850 | g_loss: 14.2280
Epoch [ 44/ 100] | d_loss: 0.3986 | g_loss: 8.7429
Epoch [ 44/ 100] | d_loss: 0.4616 | g_loss: 17.7188
Epoch [ 45/ 100] | d_loss: 1.0322 | g_loss: 11.6225
Epoch [ 45/ 100] | d_loss: 0.4518 | g_loss: 8.2310
Epoch [ 45/ 100] | d_loss: 0.5395 | g_loss: 13.5624
Epoch [ 46/ 100] | d_loss: 0.8925 | g_loss: 11.7434
Epoch [ 46/ 100] | d_loss: 0.4946 | g_loss: 9.6476
Epoch [ 46/ 100] | d_loss: 0.3597 | g_loss: 14.2146
Epoch [ 47/ 100] | d_loss: 1.6359 | g_loss: 9.1033
Epoch [ 47/ 100] | d_loss: 0.4684 | g_loss: 10.1571
Epoch [ 47/ 100] | d_loss: 0.3915 | g_loss: 12.1220
Epoch [ 48/ 100] | d_loss: 1.6015 | g_loss: 10.8328
Epoch [ 48/ 100] | d_loss: 0.4896 | g_loss: 12.4736
Epoch [ 48/ 100] | d_loss: 0.3711 | g_loss: 16.8187
Epoch [ 49/ 100] | d_loss: 1.7252 | g_loss: 13.1232
Epoch [ 49/ 100] | d_loss: 0.3986 | g_loss: 12.4418
Epoch [ 49/ 100] | d_loss: 0.3884 | g_loss: 15.6806
Epoch [ 50/ 100] | d_loss: 0.6736 | g_loss: 13.3662
Epoch [ 50/ 100] | d_loss: 0.4813 | g_loss: 8.3349
Epoch [ 50/ 100] | d_loss: 0.3528 | g_loss: 15.8811
Epoch [ 51/ 100] | d_loss: 0.5697 | g_loss: 10.5772
Epoch [ 51/ 100] | d_loss: 0.3887 | g_loss: 11.2442
Epoch [ 51/ 100] | d_loss: 0.3533 | g_loss: 21.8093
Epoch [ 52/ 100] | d_loss: 1.1224 | g_loss: 13.7392
Epoch [ 52/ 100] | d_loss: 0.4418 | g_loss: 9.4389
Epoch [ 52/ 100] | d_loss: 0.3438 | g_loss: 13.8667
Epoch [ 53/ 100] | d_loss: 0.9507 | g_loss: 13.5954
Epoch [ 53/ 100] | d_loss: 0.3734 | g_loss: 10.2547
Epoch [ 53/ 100] | d_loss: 0.3774 | g_loss: 16.8306
Epoch [ 54/ 100] | d_loss: 1.2391 | g_loss: 14.0591
Epoch [ 54/ 100] | d_loss: 0.4399 | g_loss: 15.4043
Epoch [ 54/ 100] | d_loss: 0.3683 | g_loss: 13.9010
Epoch [ 55/ 100] | d_loss: 1.0226 | g_loss: 13.8092
Epoch [ 55/ 100] | d_loss: 0.4058 | g_loss: 12.3307
Epoch [ 55/ 100] | d_loss: 0.3373 | g_loss: 14.5292
Epoch [ 56/ 100] | d_loss: 0.7458 | g_loss: 12.7015
Epoch [ 56/ 100] | d_loss: 0.6104 | g_loss: 11.0592
Epoch [ 56/ 100] | d_loss: 0.3599 | g_loss: 14.5782
Epoch [ 57/ 100] | d_loss: 0.7517 | g_loss: 14.1672
Epoch [ 57/ 100] | d_loss: 0.4376 | g_loss: 11.6036
Epoch [ 57/ 100] | d_loss: 0.3649 | g_loss: 11.8032
Epoch [ 58/ 100] | d_loss: 0.8386 | g_loss: 15.6734
Epoch [ 58/ 100] | d_loss: 0.6015 | g_loss: 10.0157
Epoch [ 58/ 100] | d_loss: 0.3409 | g_loss: 12.7498
Epoch [ 59/ 100] | d_loss: 0.7816 | g_loss: 12.8772
Epoch [ 59/ 100] | d_loss: 0.3815 | g_loss: 13.5657
Epoch [ 59/ 100] | d_loss: 0.3553 | g_loss: 16.9895
Epoch [ 60/ 100] | d_loss: 1.8105 | g_loss: 13.1576
Epoch [ 60/ 100] | d_loss: 0.5160 | g_loss: 14.5819
Epoch [ 60/ 100] | d_loss: 0.4257 | g_loss: 19.7234
Epoch [ 61/ 100] | d_loss: 0.9425 | g_loss: 11.9711
Epoch [ 61/ 100] | d_loss: 0.4487 | g_loss: 10.1208
Epoch [ 61/ 100] | d_loss: 0.3690 | g_loss: 12.6821
Epoch [ 62/ 100] | d_loss: 1.1703 | g_loss: 14.9203
Epoch [ 62/ 100] | d_loss: 0.4267 | g_loss: 12.9844
Epoch [ 62/ 100] | d_loss: 0.3522 | g_loss: 13.4276
Epoch [ 63/ 100] | d_loss: 1.1755 | g_loss: 14.1319
Epoch [ 63/ 100] | d_loss: 0.4458 | g_loss: 13.5662
Epoch [ 63/ 100] | d_loss: 0.3534 | g_loss: 14.9882
Epoch [ 64/ 100] | d_loss: 1.0760 | g_loss: 14.4738
Epoch [ 64/ 100] | d_loss: 0.4565 | g_loss: 12.1190
Epoch [ 64/ 100] | d_loss: 0.3553 | g_loss: 15.1464
Epoch [ 65/ 100] | d_loss: 0.8142 | g_loss: 11.0828
Epoch [ 65/ 100] | d_loss: 0.4330 | g_loss: 14.1257
Epoch [ 65/ 100] | d_loss: 0.3599 | g_loss: 15.4030
Epoch [ 66/ 100] | d_loss: 0.6770 | g_loss: 13.1254
Epoch [ 66/ 100] | d_loss: 0.5536 | g_loss: 13.1232
Epoch [ 66/ 100] | d_loss: 0.3725 | g_loss: 12.5105
Epoch [ 67/ 100] | d_loss: 0.6099 | g_loss: 12.6813
Epoch [ 67/ 100] | d_loss: 0.6119 | g_loss: 11.8948
Epoch [ 67/ 100] | d_loss: 0.3643 | g_loss: 13.8359
Epoch [ 68/ 100] | d_loss: 0.8602 | g_loss: 13.3447
Epoch [ 68/ 100] | d_loss: 0.6922 | g_loss: 16.1481
Epoch [ 68/ 100] | d_loss: 0.3522 | g_loss: 15.6391
Epoch [ 69/ 100] | d_loss: 1.3279 | g_loss: 13.6985
Epoch [ 69/ 100] | d_loss: 0.4594 | g_loss: 13.2752
Epoch [ 69/ 100] | d_loss: 0.3806 | g_loss: 11.9751
Epoch [ 70/ 100] | d_loss: 0.7558 | g_loss: 13.9299
Epoch [ 70/ 100] | d_loss: 0.4122 | g_loss: 14.1247
Epoch [ 70/ 100] | d_loss: 0.3731 | g_loss: 14.1739
Epoch [ 71/ 100] | d_loss: 0.6188 | g_loss: 15.3189
Epoch [ 71/ 100] | d_loss: 0.4105 | g_loss: 16.1061
Epoch [ 71/ 100] | d_loss: 0.3339 | g_loss: 16.0961
Epoch [ 72/ 100] | d_loss: 0.7347 | g_loss: 14.8844
Epoch [ 72/ 100] | d_loss: 0.6053 | g_loss: 11.8251
Epoch [ 72/ 100] | d_loss: 0.4238 | g_loss: 14.9223
Epoch [ 73/ 100] | d_loss: 1.1834 | g_loss: 15.3078
Epoch [ 73/ 100] | d_loss: 0.5181 | g_loss: 12.1415
Epoch [ 73/ 100] | d_loss: 0.3445 | g_loss: 14.8677
Epoch [ 74/ 100] | d_loss: 0.8008 | g_loss: 13.1710
Epoch [ 74/ 100] | d_loss: 0.4513 | g_loss: 15.9446
Epoch [ 74/ 100] | d_loss: 0.4414 | g_loss: 20.3710
Epoch [ 75/ 100] | d_loss: 1.2803 | g_loss: 15.4193
Epoch [ 75/ 100] | d_loss: 0.5942 | g_loss: 10.7087
Epoch [ 75/ 100] | d_loss: 0.3437 | g_loss: 17.9181
Epoch [ 76/ 100] | d_loss: 1.0286 | g_loss: 12.8885
Epoch [ 76/ 100] | d_loss: 0.4920 | g_loss: 18.6149
Epoch [ 76/ 100] | d_loss: 0.3751 | g_loss: 17.4362
Epoch [ 77/ 100] | d_loss: 0.9973 | g_loss: 17.9688
Epoch [ 77/ 100] | d_loss: 0.4018 | g_loss: 15.8639
Epoch [ 77/ 100] | d_loss: 0.3448 | g_loss: 16.8935
Epoch [ 78/ 100] | d_loss: 1.0238 | g_loss: 14.3503
Epoch [ 78/ 100] | d_loss: 0.4841 | g_loss: 15.9601
Epoch [ 78/ 100] | d_loss: 0.3357 | g_loss: 15.6731
Epoch [ 79/ 100] | d_loss: 0.9124 | g_loss: 14.2594
Epoch [ 79/ 100] | d_loss: 0.3902 | g_loss: 14.8787
Epoch [ 79/ 100] | d_loss: 0.3434 | g_loss: 17.8774
Epoch [ 80/ 100] | d_loss: 0.7669 | g_loss: 14.9693
Epoch [ 80/ 100] | d_loss: 0.3639 | g_loss: 20.3815
Epoch [ 80/ 100] | d_loss: 0.3442 | g_loss: 13.0722
Epoch [ 81/ 100] | d_loss: 1.0707 | g_loss: 14.3246
Epoch [ 81/ 100] | d_loss: 0.4075 | g_loss: 17.0175
Epoch [ 81/ 100] | d_loss: 0.3697 | g_loss: 18.8611
Epoch [ 82/ 100] | d_loss: 1.0980 | g_loss: 14.5868
Epoch [ 82/ 100] | d_loss: 0.4924 | g_loss: 19.5658
Epoch [ 82/ 100] | d_loss: 0.3424 | g_loss: 12.9414
Epoch [ 83/ 100] | d_loss: 0.9112 | g_loss: 17.5380
Epoch [ 83/ 100] | d_loss: 0.3837 | g_loss: 20.3259
Epoch [ 83/ 100] | d_loss: 0.3333 | g_loss: 18.1492
Epoch [ 84/ 100] | d_loss: 0.6574 | g_loss: 16.3081
Epoch [ 84/ 100] | d_loss: 0.4217 | g_loss: 17.3476
Epoch [ 84/ 100] | d_loss: 0.3554 | g_loss: 18.8399
Epoch [ 85/ 100] | d_loss: 0.8820 | g_loss: 17.5911
Epoch [ 85/ 100] | d_loss: 0.4262 | g_loss: 16.1993
Epoch [ 85/ 100] | d_loss: 0.3485 | g_loss: 14.7559
Epoch [ 86/ 100] | d_loss: 0.4581 | g_loss: 16.3607
Epoch [ 86/ 100] | d_loss: 0.4308 | g_loss: 16.9571
Epoch [ 86/ 100] | d_loss: 0.3995 | g_loss: 15.4270
Epoch [ 87/ 100] | d_loss: 0.6950 | g_loss: 14.6800
Epoch [ 87/ 100] | d_loss: 0.4876 | g_loss: 19.5503
Epoch [ 87/ 100] | d_loss: 0.3796 | g_loss: 14.6323
Epoch [ 88/ 100] | d_loss: 0.8164 | g_loss: 16.1642
Epoch [ 88/ 100] | d_loss: 0.4529 | g_loss: 17.5407
Epoch [ 88/ 100] | d_loss: 0.3481 | g_loss: 15.0995
Epoch [ 89/ 100] | d_loss: 0.4253 | g_loss: 14.2475
Epoch [ 89/ 100] | d_loss: 0.4663 | g_loss: 20.7928
Epoch [ 89/ 100] | d_loss: 0.3493 | g_loss: 12.6848
Epoch [ 90/ 100] | d_loss: 0.6324 | g_loss: 14.3659
Epoch [ 90/ 100] | d_loss: 0.3564 | g_loss: 14.4839
Epoch [ 90/ 100] | d_loss: 0.3456 | g_loss: 13.2325
Epoch [ 91/ 100] | d_loss: 0.4724 | g_loss: 12.8062
Epoch [ 91/ 100] | d_loss: 0.4218 | g_loss: 15.9515
Epoch [ 91/ 100] | d_loss: 0.3742 | g_loss: 14.1208
Epoch [ 92/ 100] | d_loss: 0.5828 | g_loss: 14.9528
Epoch [ 92/ 100] | d_loss: 0.4663 | g_loss: 17.1954
Epoch [ 92/ 100] | d_loss: 0.3966 | g_loss: 15.6063
Epoch [ 93/ 100] | d_loss: 0.3877 | g_loss: 18.0134
Epoch [ 93/ 100] | d_loss: 0.4227 | g_loss: 16.2912
Epoch [ 93/ 100] | d_loss: 0.3556 | g_loss: 14.5541
Epoch [ 94/ 100] | d_loss: 0.3899 | g_loss: 17.4970
Epoch [ 94/ 100] | d_loss: 0.5194 | g_loss: 17.1904
Epoch [ 94/ 100] | d_loss: 0.3436 | g_loss: 12.9894
Epoch [ 95/ 100] | d_loss: 0.6292 | g_loss: 17.2345
Epoch [ 95/ 100] | d_loss: 0.4242 | g_loss: 16.9986
Epoch [ 95/ 100] | d_loss: 0.3520 | g_loss: 16.3274
Epoch [ 96/ 100] | d_loss: 0.4138 | g_loss: 12.0211
Epoch [ 96/ 100] | d_loss: 0.3920 | g_loss: 16.1397
Epoch [ 96/ 100] | d_loss: 0.3473 | g_loss: 17.8238
Epoch [ 97/ 100] | d_loss: 0.7130 | g_loss: 16.0466
Epoch [ 97/ 100] | d_loss: 0.4132 | g_loss: 17.5734
Epoch [ 97/ 100] | d_loss: 0.3350 | g_loss: 15.7057
Epoch [ 98/ 100] | d_loss: 0.6129 | g_loss: 18.6339
Epoch [ 98/ 100] | d_loss: 0.3829 | g_loss: 17.1675
Epoch [ 98/ 100] | d_loss: 0.3422 | g_loss: 17.0065
Epoch [ 99/ 100] | d_loss: 0.6298 | g_loss: 16.4161
Epoch [ 99/ 100] | d_loss: 0.3821 | g_loss: 16.3967
Epoch [ 99/ 100] | d_loss: 0.3362 | g_loss: 14.8846
Epoch [ 100/ 100] | d_loss: 0.4717 | g_loss: 16.5175
Epoch [ 100/ 100] | d_loss: 0.4092 | g_loss: 18.5726
Epoch [ 100/ 100] | d_loss: 0.3331 | g_loss: 15.4866
# 绘图
fig, ax = plt.subplots()
losses = np.array(losses)
plt.plot(losses.T[0], label='Discriminator')
plt.plot(losses.T[1], label='Generator')
plt.title("Training Losses")
plt.legend()
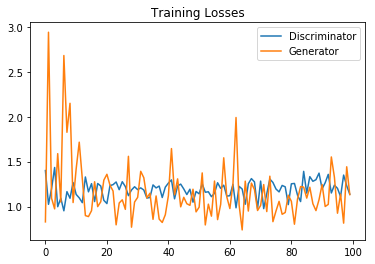
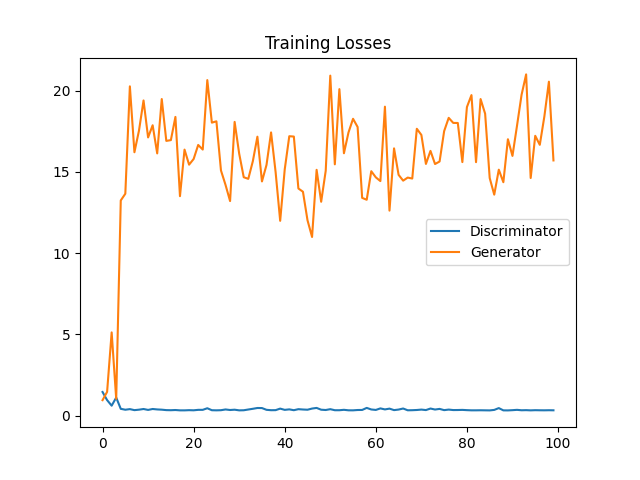
生成网络效果有点差


