Ascend C算子
一、AICORE内部支持核心计算:标量、向量和矩阵计算
标量计算
int x=0,y=0;
int z=x+y;
向量计算
int x[1024],y[1024],z[1024];
Add(z,x,y,1024);//z=x+y;
矩阵计算
C=A*B
Mmad(C,A,B,M,K,N);
SIMD:单指令多数据计算(一条指令可以处理多个数据)
Ascend C编程API主要是向量计算API和矩阵计算API,计算API都是SIMD样式,从而达到加速计算的目的
二、并行计算
了解一下指令流水线
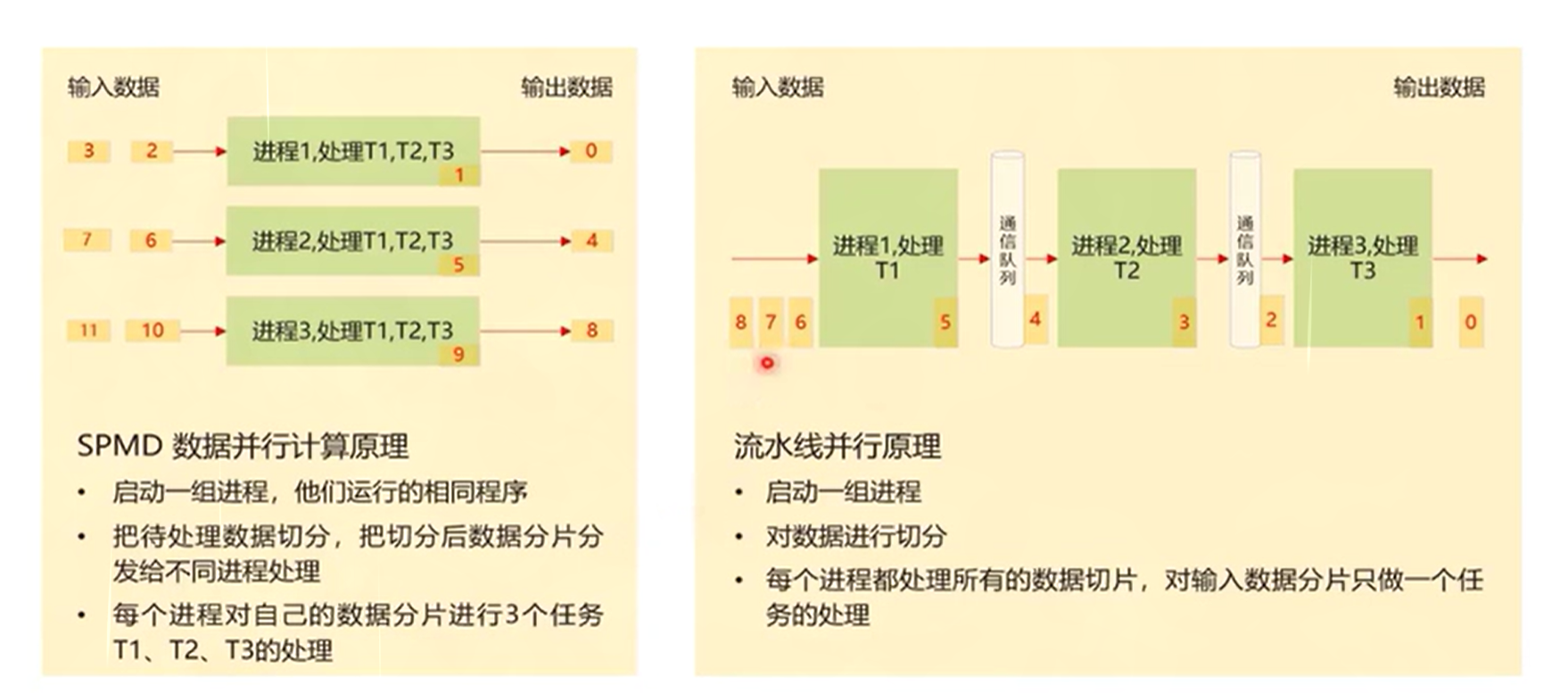
单程序多数据:SPMD每组数据都是独立的
流水线:不同的任务之间都会有数据在执行并且处理
三、基于SPMD编程


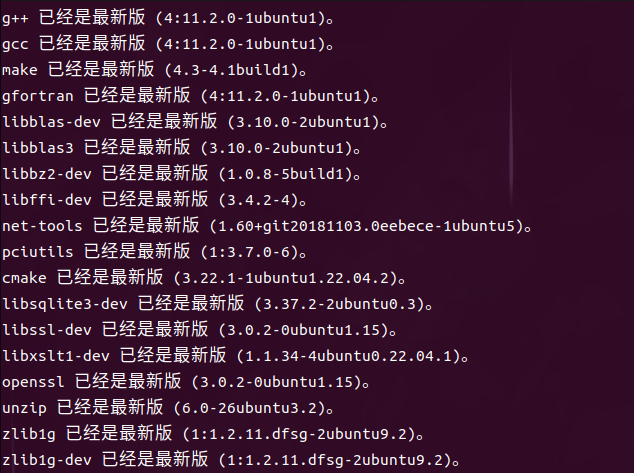
四、环境配置
五、流程和问题
权限不够
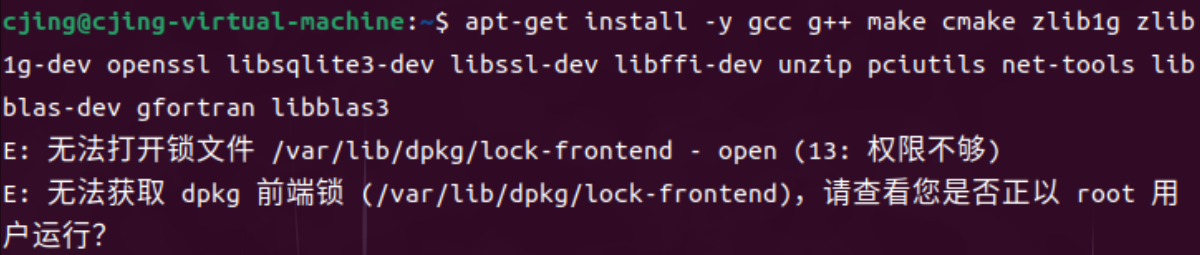
加上 sudo
无法定位软件包
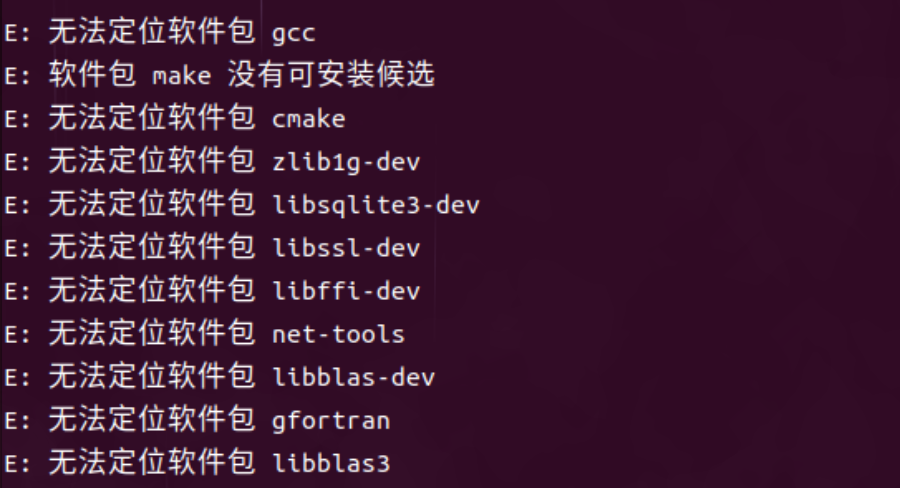
权限报错

WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/ven
更换介质

注释掉第一行
无法下载

修改umask 0027
把下载文件换一个文件夹
cmake版本问题
更新之后反而运行不了
成功运行
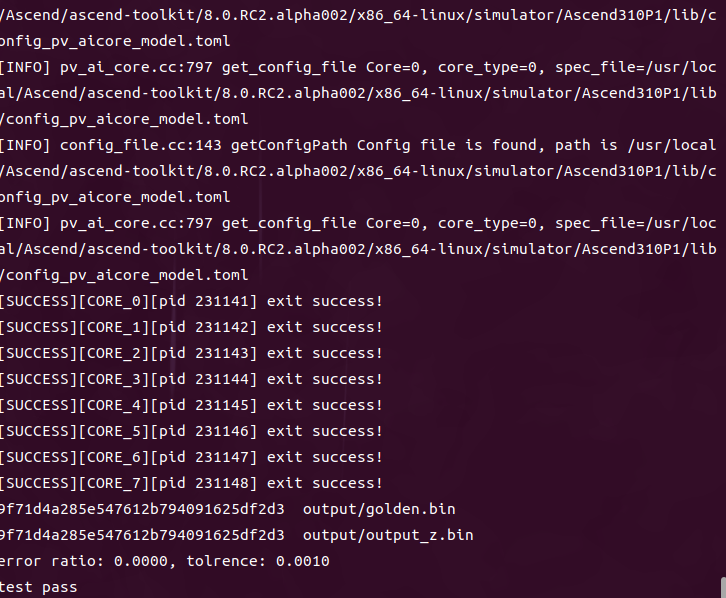
六、编程范式
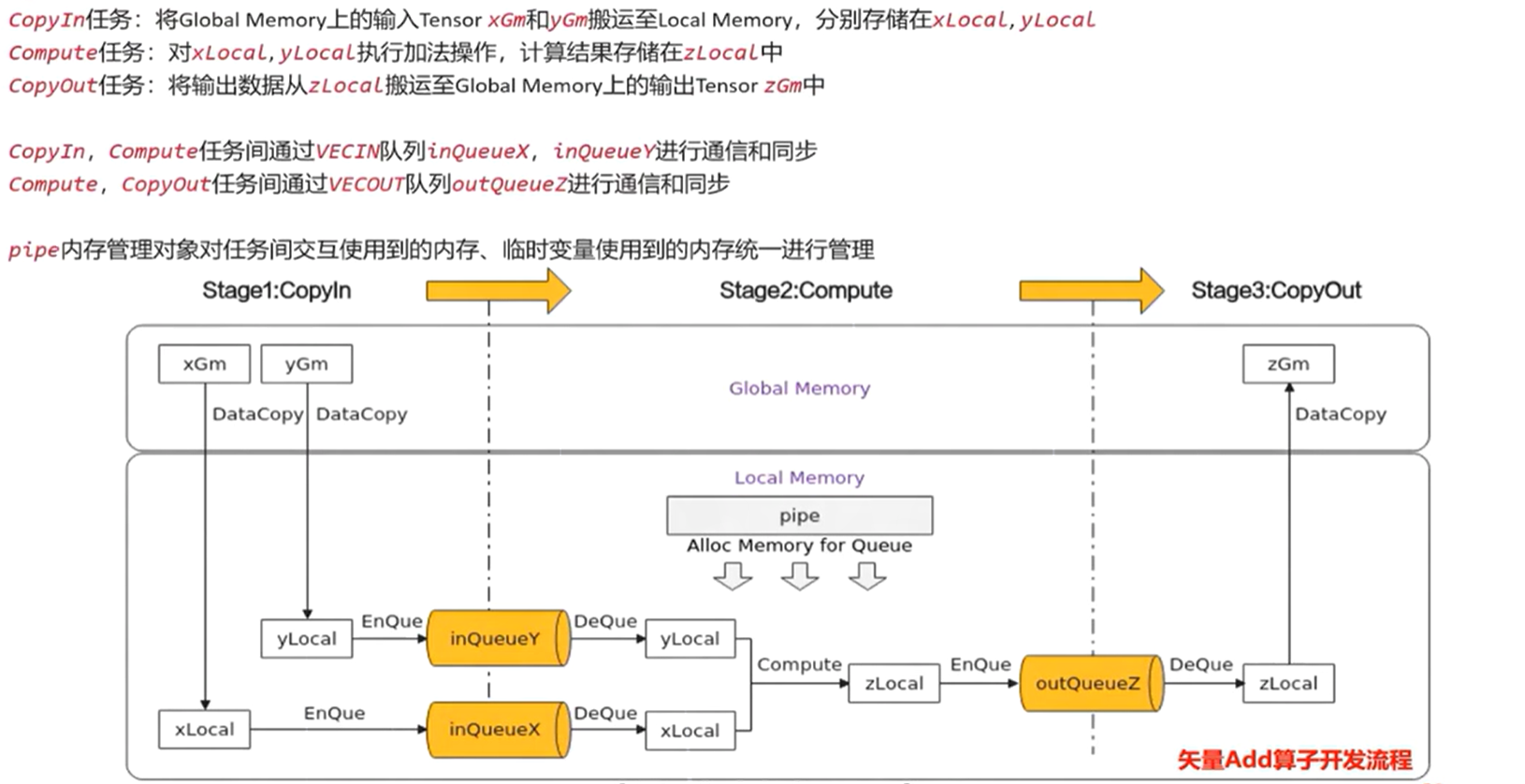
1、把算子内部的处理程序,分成多个流水任务(stage)
2、以张量(tensor)为数据载体
3、以队列(queue)进行任务之间的通信与同步
4、以内存管理模块(pipe)管理任务间的通信内存
6.1 抽象编程模型
1、Ascend C的并行编程范式核心要素
- 一组并行计算任务
- 通过队列实现任务之间的通信和同步
- 程序员自主表达对并行计算任务和资源的调度
2、典型的计算范式
- 基本的矢量编程范式:计算任务分为CopyIn,Compute,CopyOut
- 基本的矩阵编程范式:计算任务分为文案CopyIn,Split,Compute,Aggregate,CopyOut
- 复杂的矢量/矩阵编程范式,通过将矢量/矩阵的Out/In组合在一起的方式来实现复杂计算数据流
6.2 流水任务
流水任务(Stage)指的是单核处理程序中主程序调度的并行任务。
在核函数内部,可以通过流水任务实现数据的并行处理来提升性能。
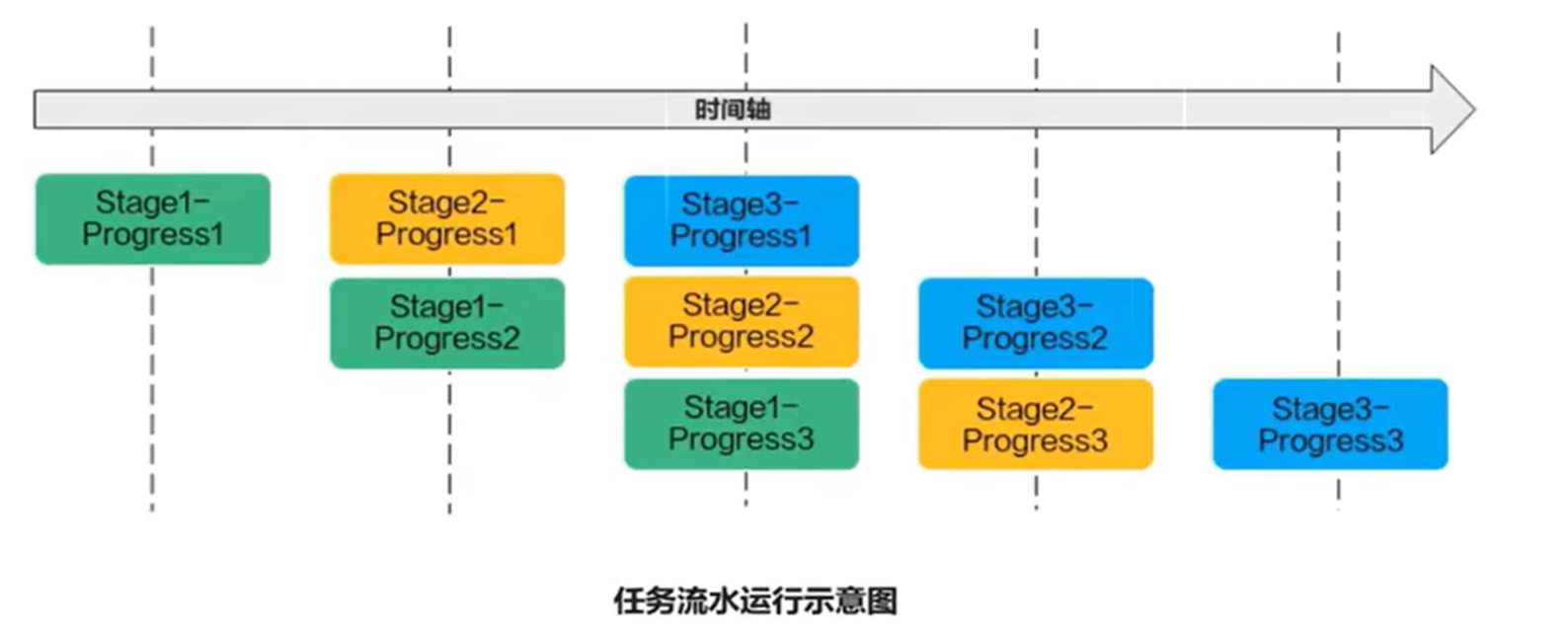
6.3 矢量编程流水任务设计

6.4 任务间通信和同步

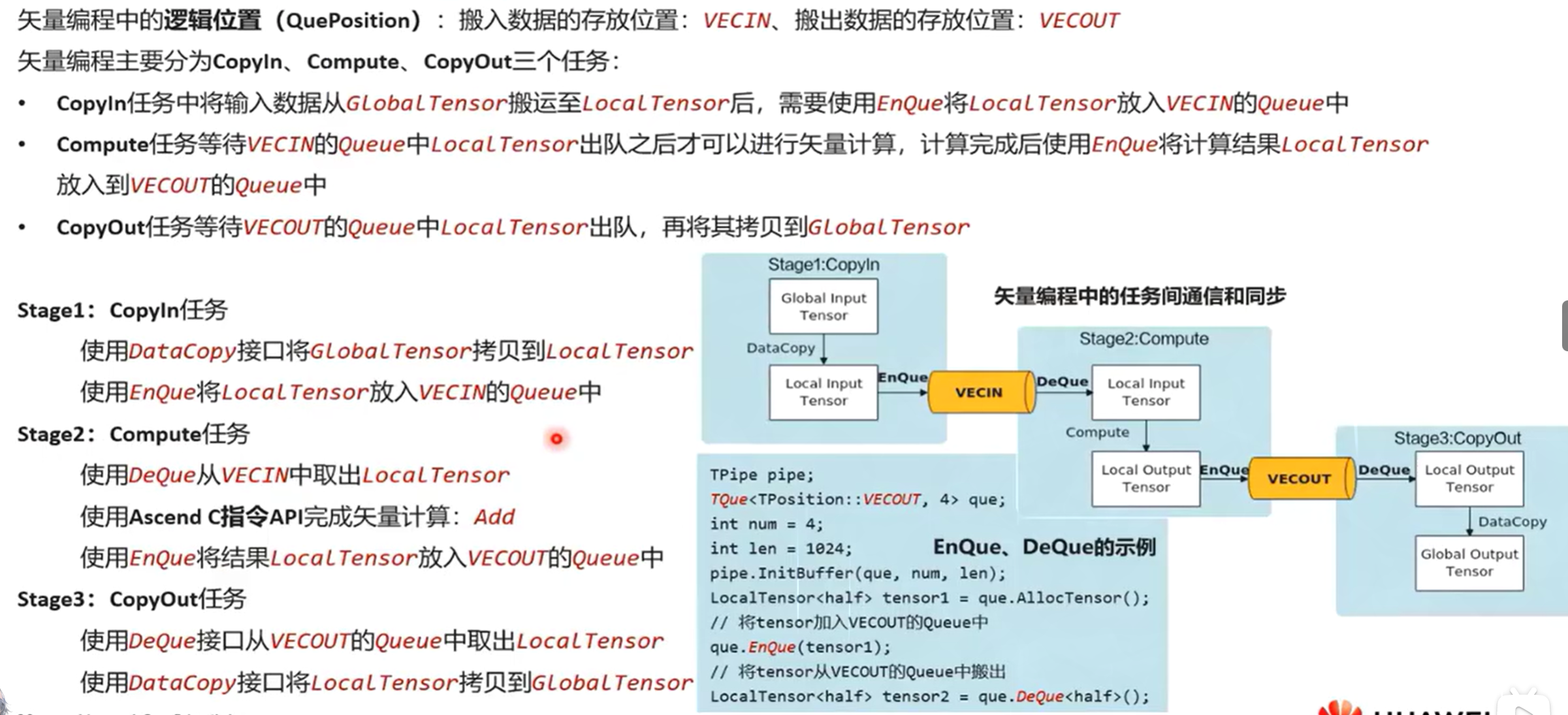
用队列实现同步
6.5 内存管理
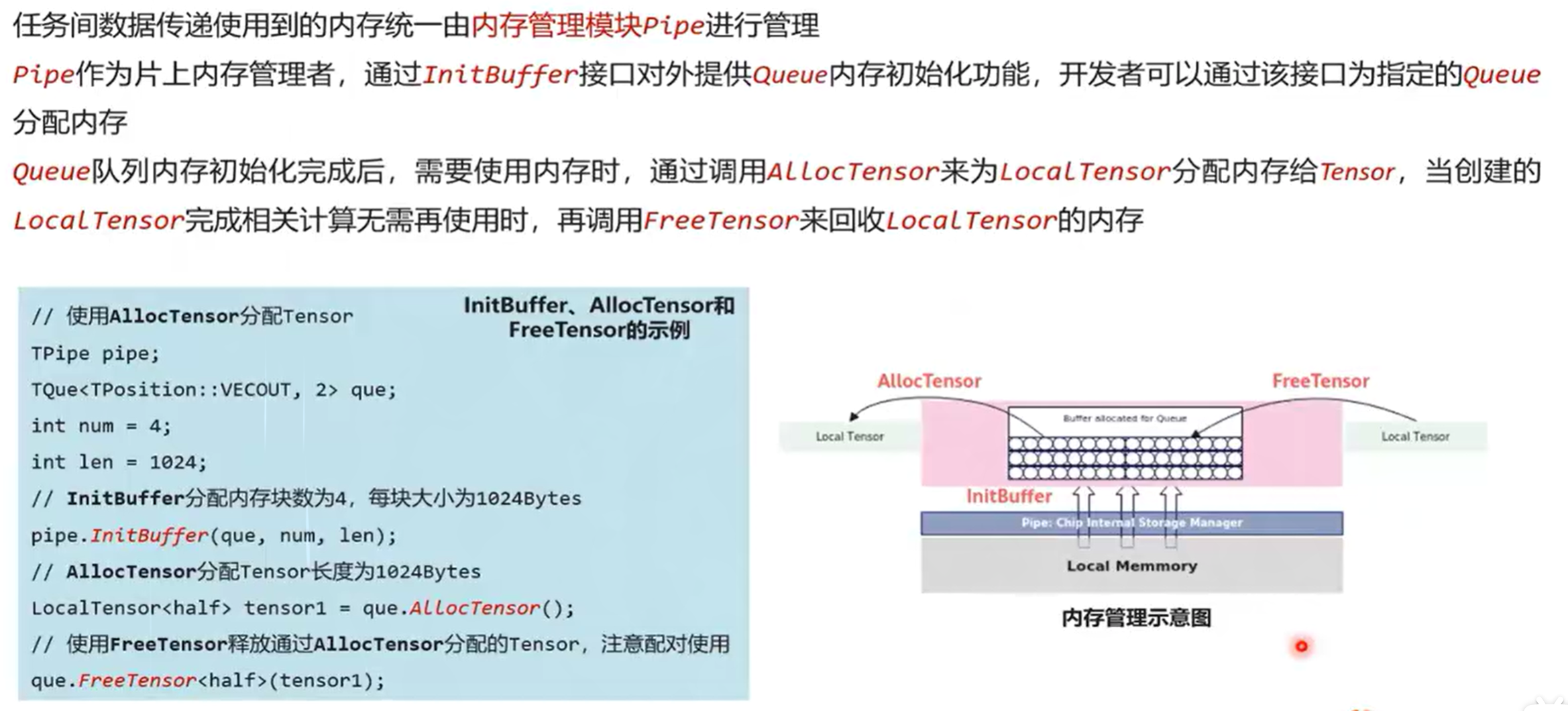
AllocTensor和FreeTensor一起用,分配和回收内存
6.6 临时变量内存管理

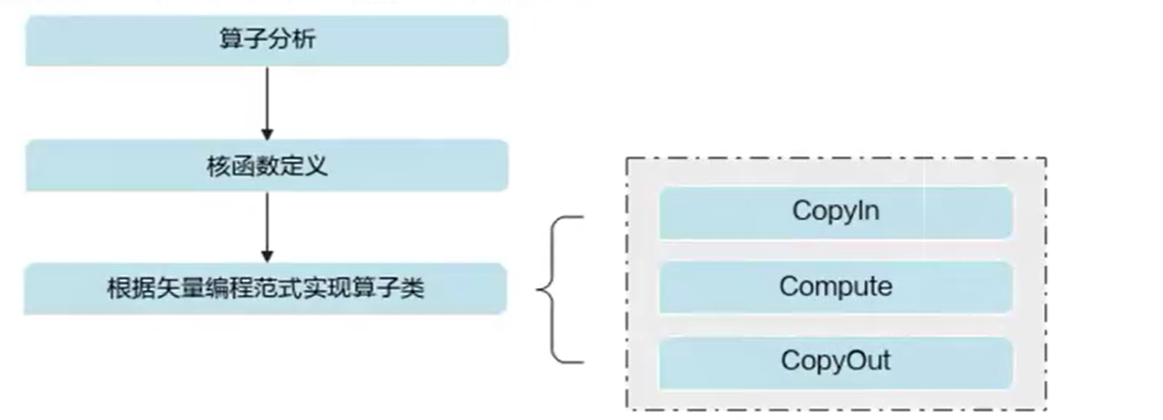
6.7 开发流程
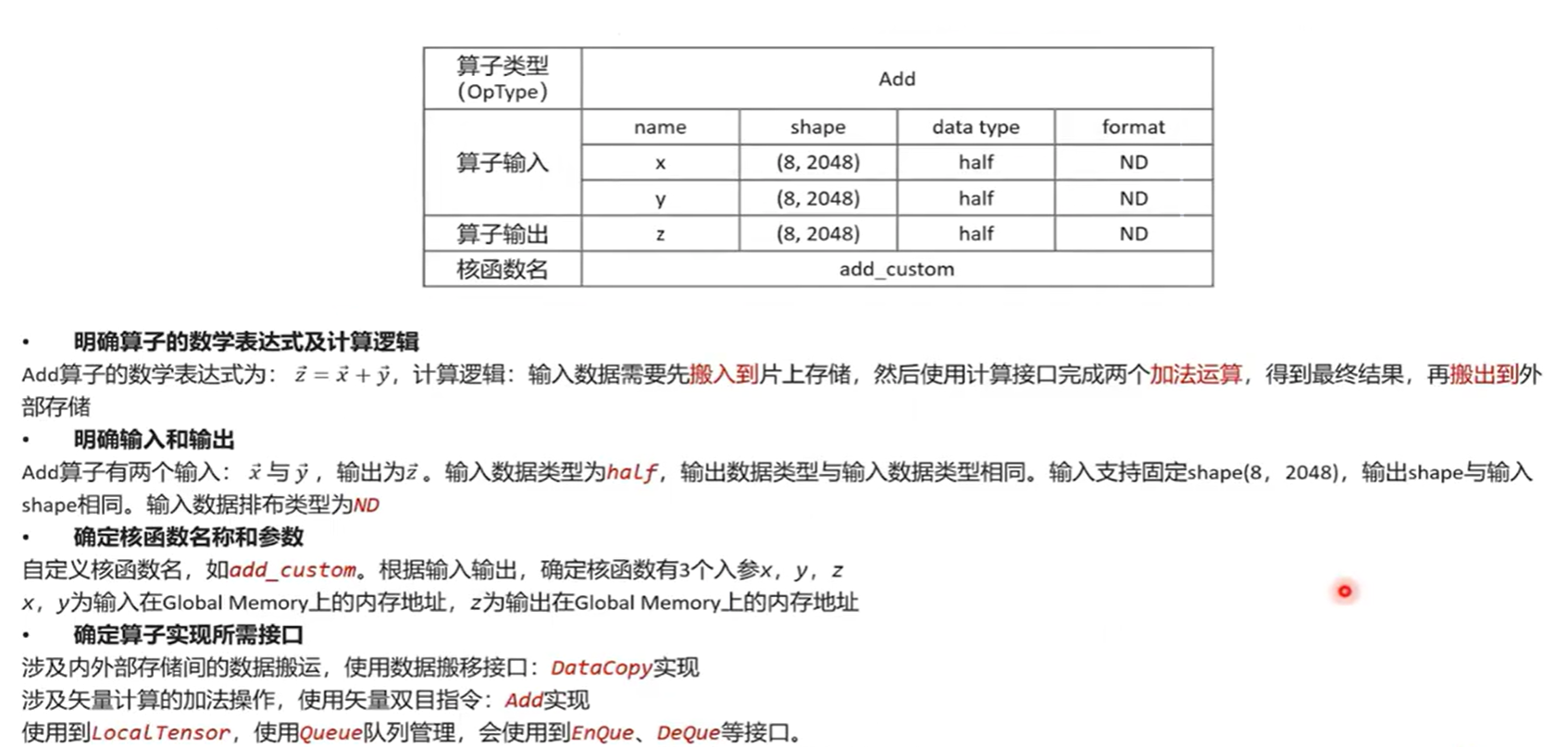
算子分析:分析算子的数学表达式、输入、输出以及计算逻辑的实现,明确需要调用的Ascend C接口。
核函数定义:定义Ascend C算子入口函数。
根据矢量编程范式实现算子类:完成核函数的内部实现

6.8 算子实现
核函数定义
1、实例化算子类,调用\(Init()\)函数完成内存初始化,调用\(Process()\)函数完成核心逻辑
算子类名核成员函数名无特殊要求,可根据C/C++编码习惯决定核函数中的具体表现
//implementation of kernel function
extern "C" __global__ __aicore__ void add_custom(__gm__uint8_t* x,__gm__uint8_t* y,__gm__uint8_t* z)
{
KernelAdd op;
op.Init(x,y,z);
op.Process();
}
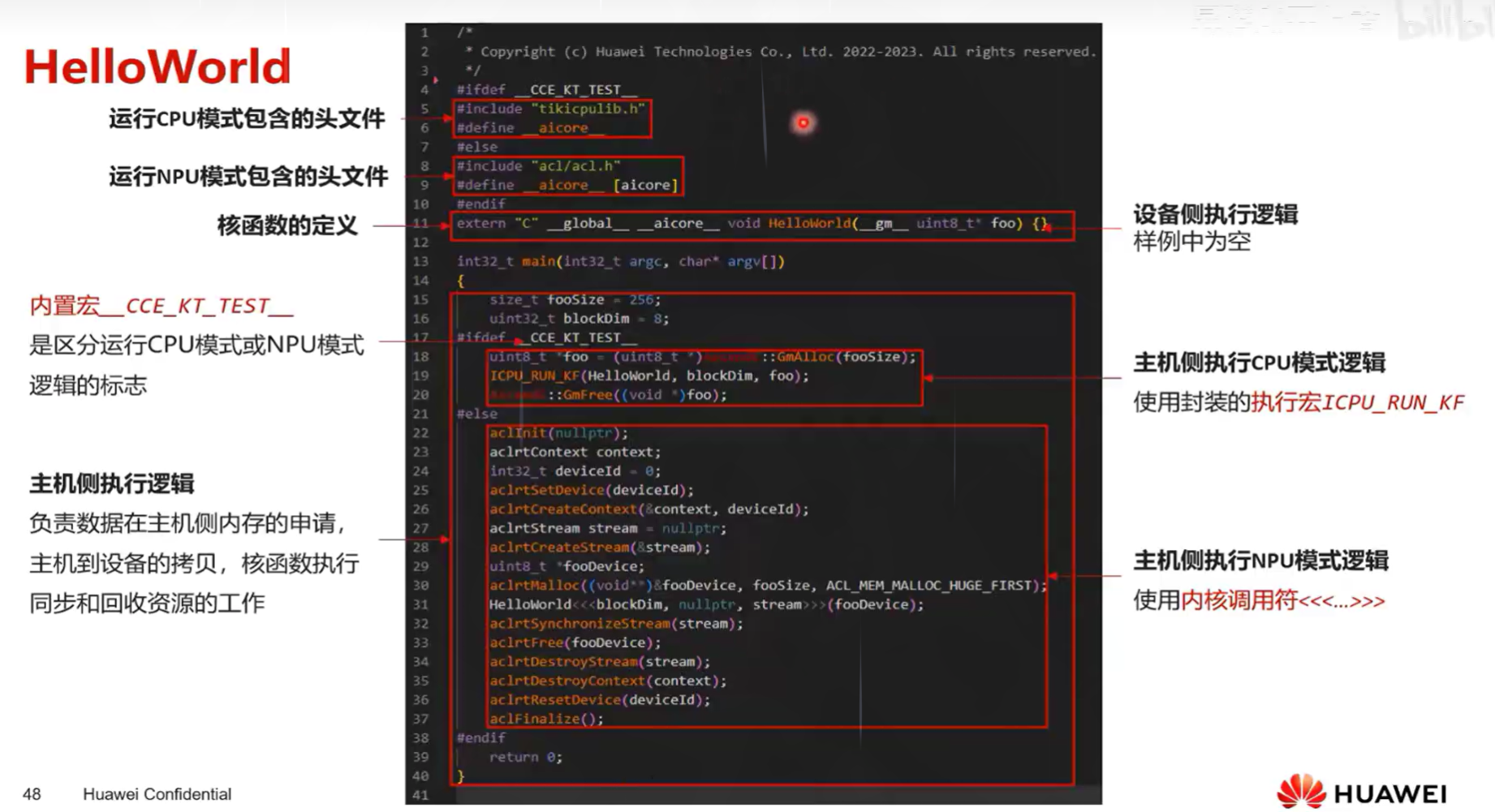
2、核函数的调用,内置宏__CCE_KT_TEST__来标识<<<...>>>,对核函数的调用进行封装,可以在封装函数中补充其他逻辑
用内置宏区分NPU模式和CPU模式(g++没有<<<>>>表达)
#ifndef __CCE_KT_TEST__
//call of kernel function
void add_custom_do(uint32_t blockDim,void* l2ctrl,void* stream,uint8_t* x,uint8_t* y,uint8_t* z)
{
add_custom<<<blockDim,l2ctrl,stream>>>(x,y,z);
}
#endif
如果是 if not defined (ifndef 如上),不包含宏,会走NPU的模式
如果是 if defined ,则仅在CPU模式下进行编译
样例
七、Tiling计算
7.1 基本概念

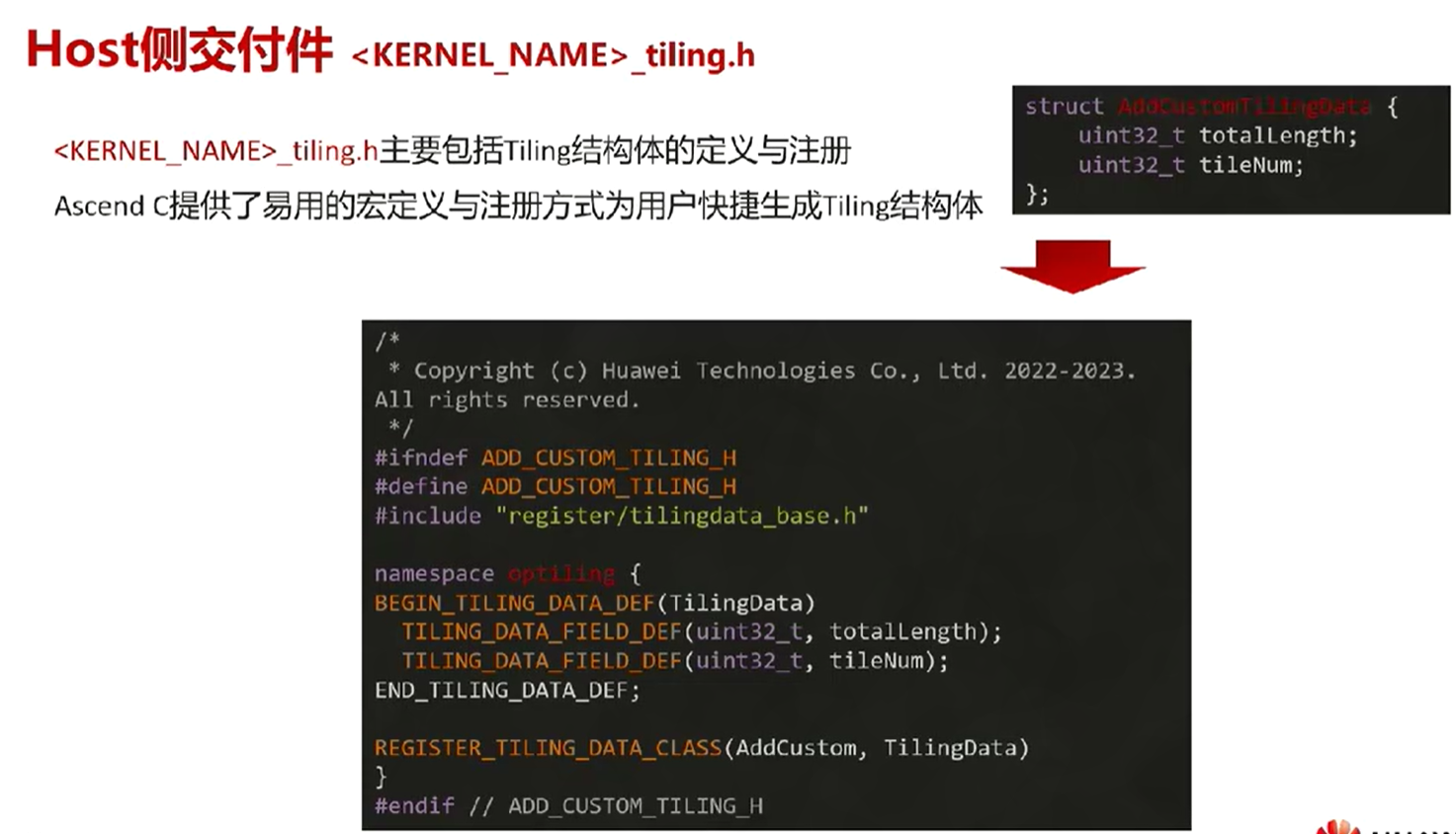
struct AddCustomTilingData{
uint32_t totalLength;//算子长度 shape
uint32_t tileNum;//切片个数 切块的策略
}
固定shape:输入大小都是已知的,每次搬运多少数据、总共需要搬运多少次均可以在编译时直接计算出来(算子shape固定时,开发者使用不同shape时需要重新对算子进行编译,带来大量的算子二进制文件)
动态shape:算子可以将形状通过核函数的入参传入核函数内,参与内部逻辑计算,从而符合不同shape下的使用场景
| 区分 | 固定shape | 动态shape |
|---|---|---|
| 使用场景 | 输入shape固定不变的场景 | 输入shape频繁变动的场景 |
| 实现难度 | 低,只需要考虑shape的逻辑处理 | 高,需要考虑shape带来的不同逻辑的分支处理 |
| 优化难度 | 低,AI编译器可以进行更多优化 | 高,AI编译器对于未知数据采取保守策略 |
7.2 固态shape场景的Tiling实现

7.3 动态shape场景的Tiling实现
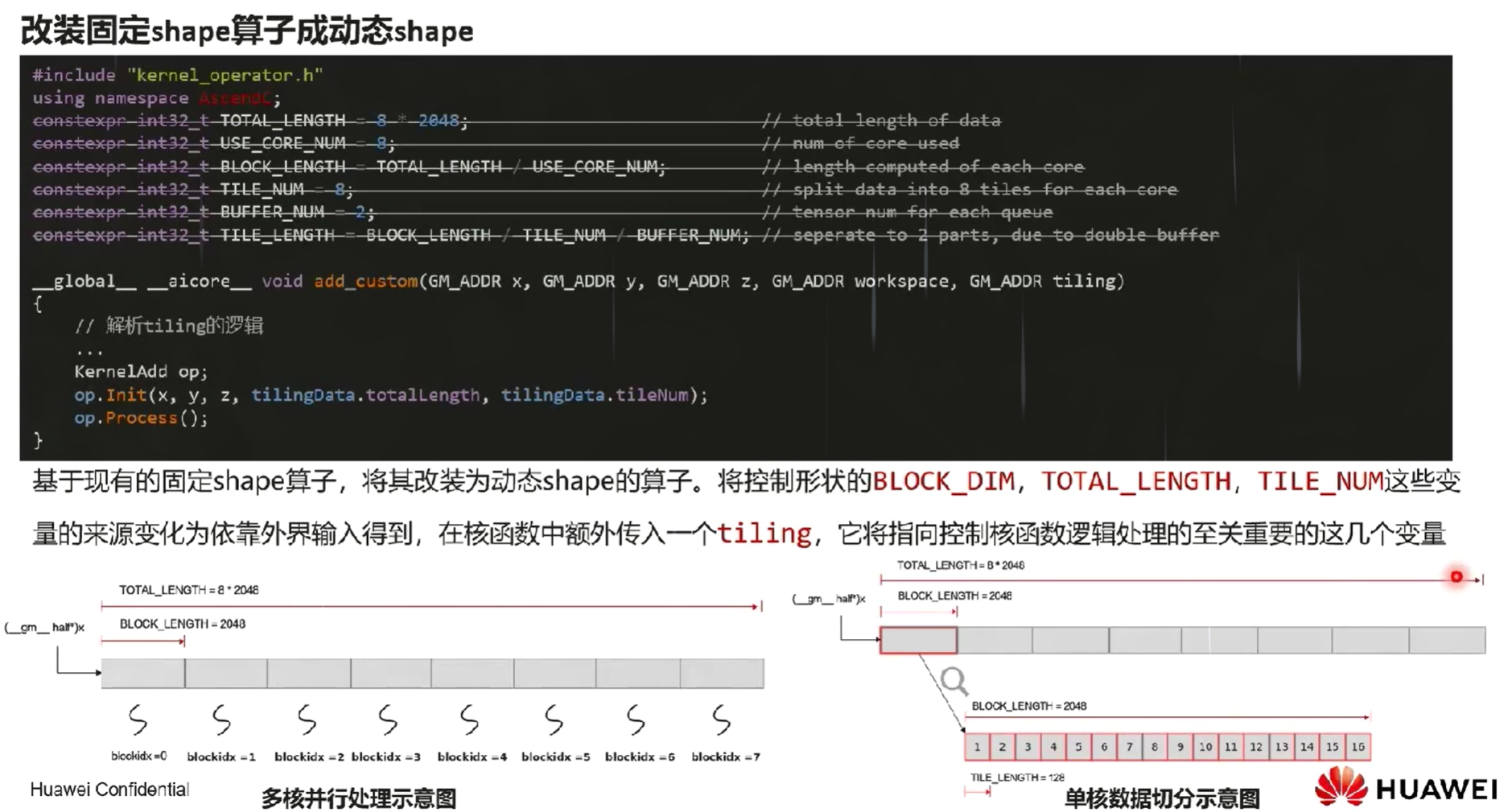

7.4 固态与动态shape场景的Tiling实现
样例对比
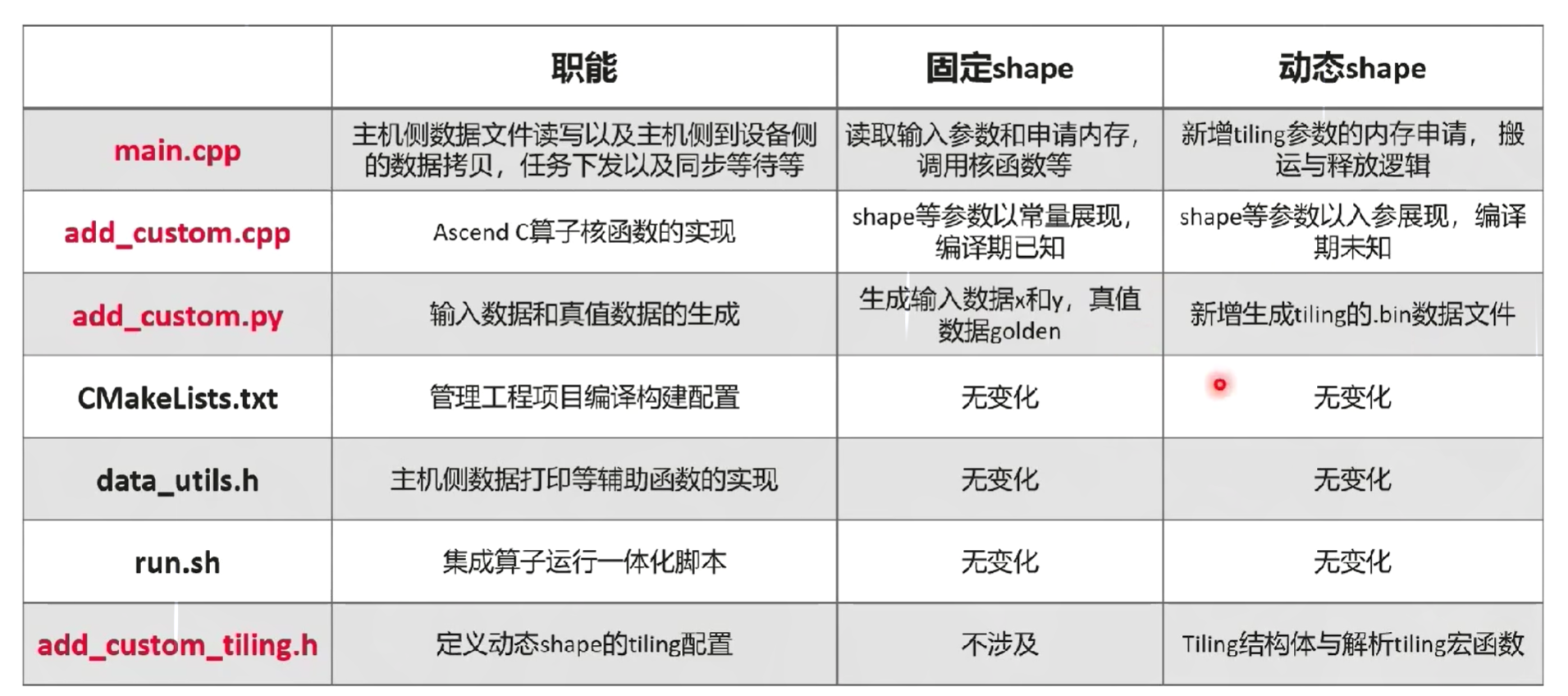
八、算子调试
CPU和NPU孪生调试
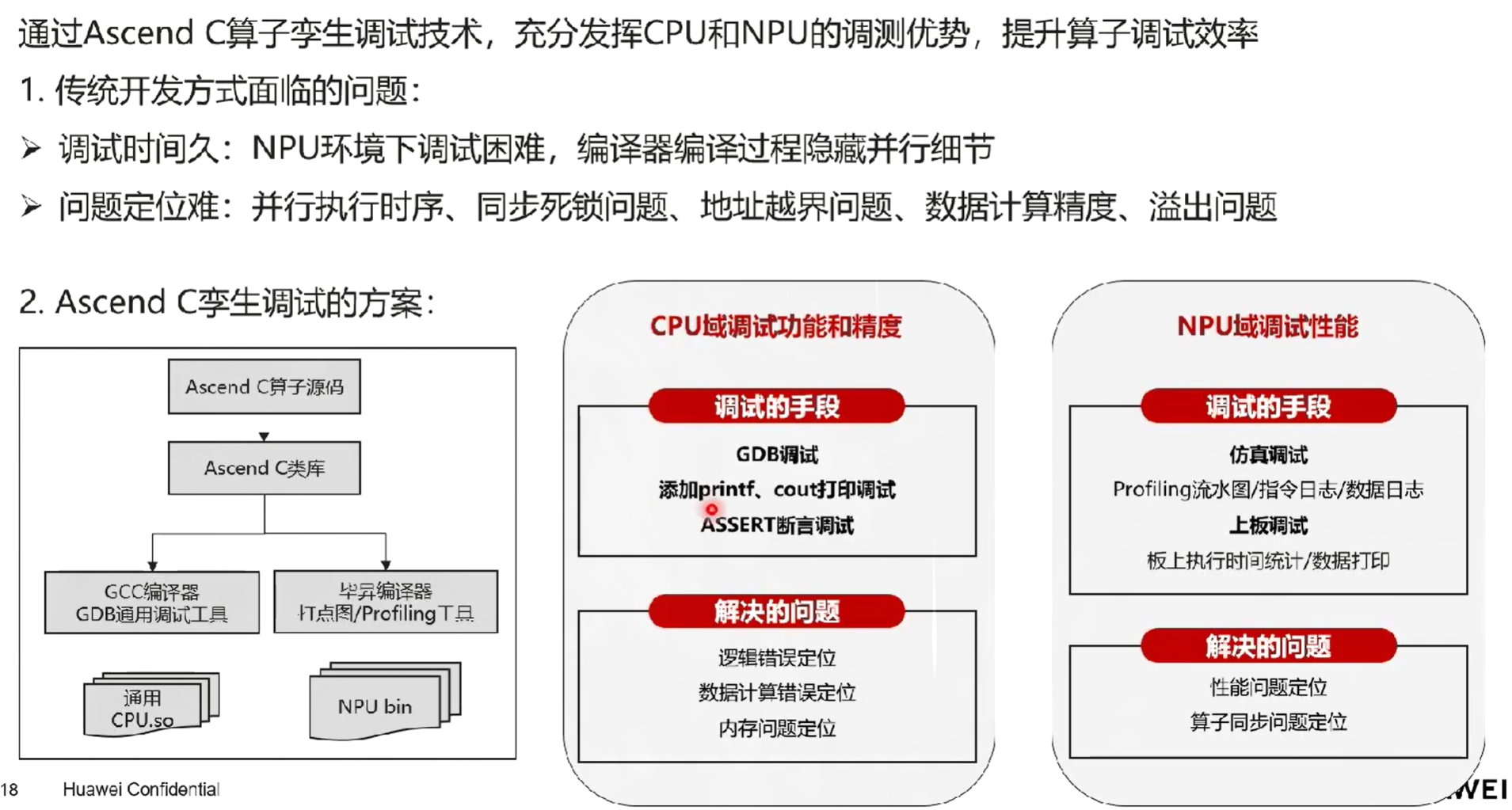
CPU模式下的算子调试
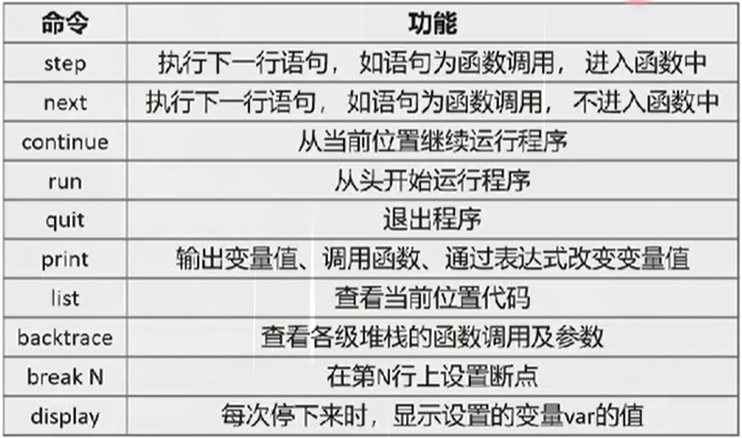
1. 使用GDB进行调试
2. 使用print或者std::cout
在CPU代码侧直接插入C/C++的打印命令,如printf、std::cout,由于NPU模式目前不支持打印语句,所以需要添加内置宏__CCE_KT_TEST__予以区分
NPU模式下的算子调试
九、算子交付件
主要分为host侧交付件和device侧交付件
实际的编译过程中
- host侧会用传统的C/C++编译器来进行编译,如gcc/g++或clang/clang++
- device侧会用自研的编译器进行编译,编译成的二进制会分别被host和device所调用执行
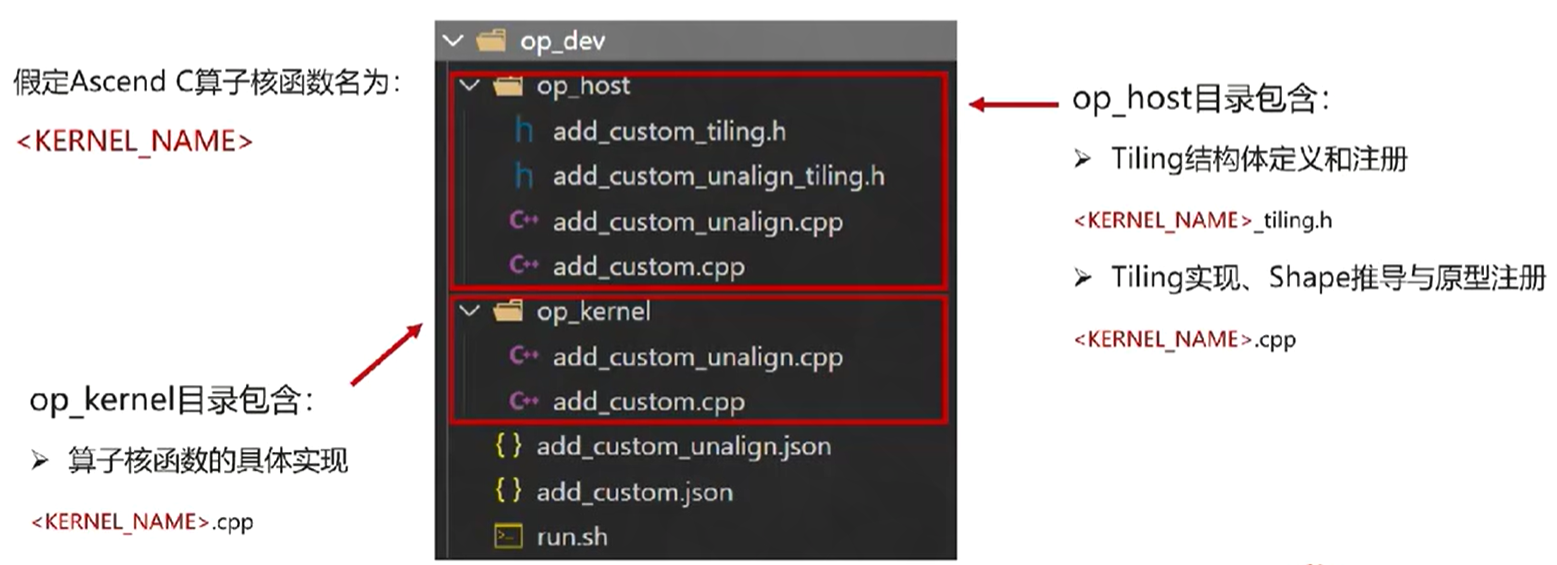
1. Host侧交付件
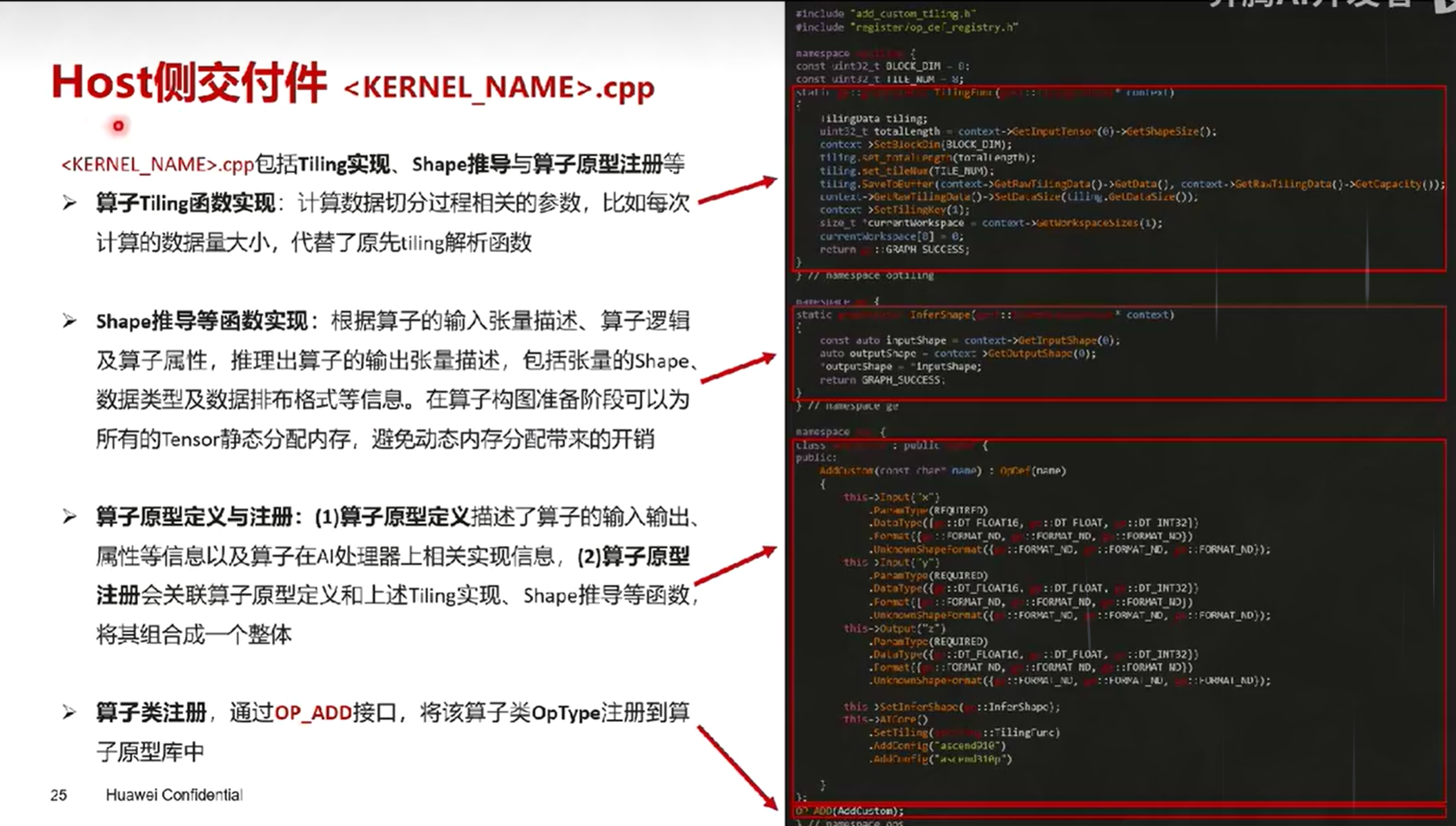
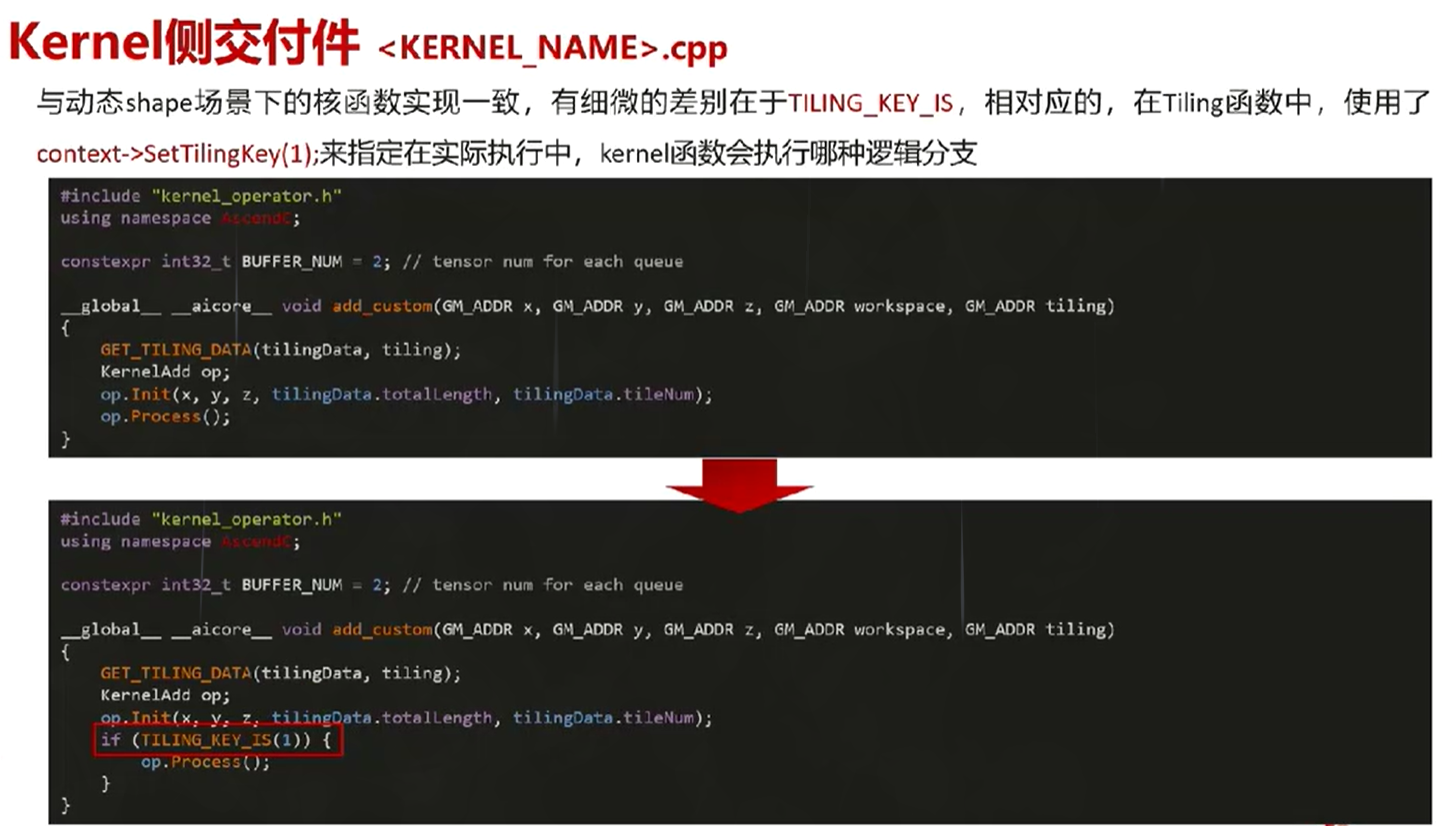
2. Kernel侧交付件
3. 更多交付件
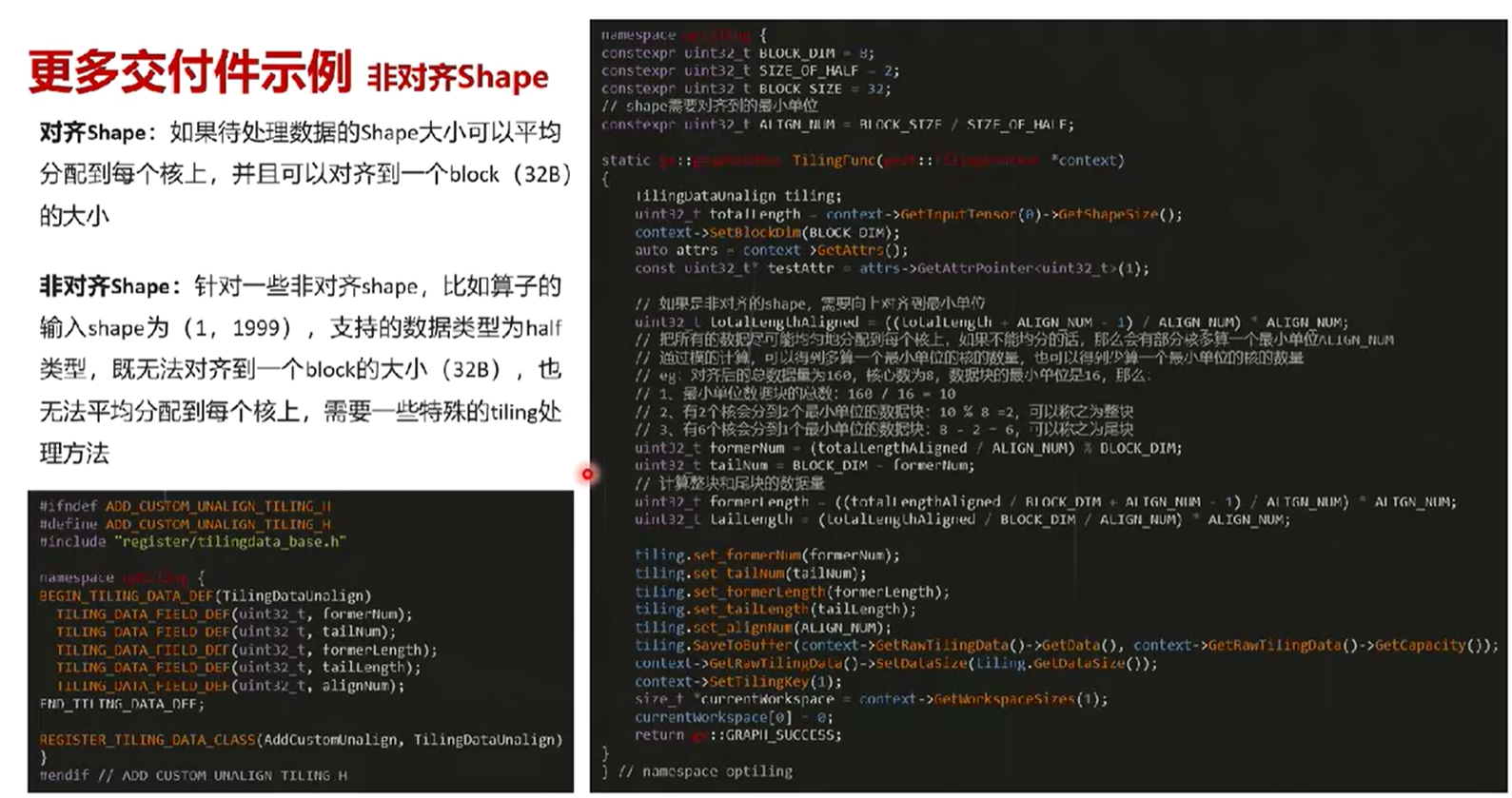
十、自定义算子工程
1. 介绍
自定义算子工程:一个包含用户编写的host侧和kernel侧算子实现文件的,用于编译和安装自定义算子run包的工程框架
- 通过编译自定义算子工程,可以生成算子的二进制文件,并将算子适配插件,工程配置文件等一起打到run包中
- 通过部署自定义算子run包,用户可以快速地把算子集成到安装好的CANN算子库中,从而在应用程序中进行调用
AddCustom
|—————— build.sh // 编译入口脚本
|—————— cmake // CMake编译文件
| |—————— config.cmake
| |—————— util // 算子工程编译所需脚本及公共编译文件存放目录
|—————— CMakeLists.txt // 算子工程的CMakeLists.txt CMake编译配置文件
|—————— CMakePresets.json // 编译配置项
|—————— framework // 算子插件实现目录,单算子模型文件的生成不依赖算子适配插件,无需关注
|—————— op_host // host侧实现文件
| |—————— add_custom_tiling.h // 算子tiling定义文件
| |—————— add_custom.cpp // 算子原型注册、shape推导、信息库、tiling实现等内容文件
| |—————— CMakeLists.txt
|—————— op_kernel // kernel侧实现文件
| |—————— CMakeLists.txt
| |—————— add_custom.cpp // 算子代码实现文件
|—————— scripts // 自定义算子工程打包相关脚本所在目录
标准流程:按照工程创建->算子实现->编译部署->算子调用的流程完成算子开发和调用
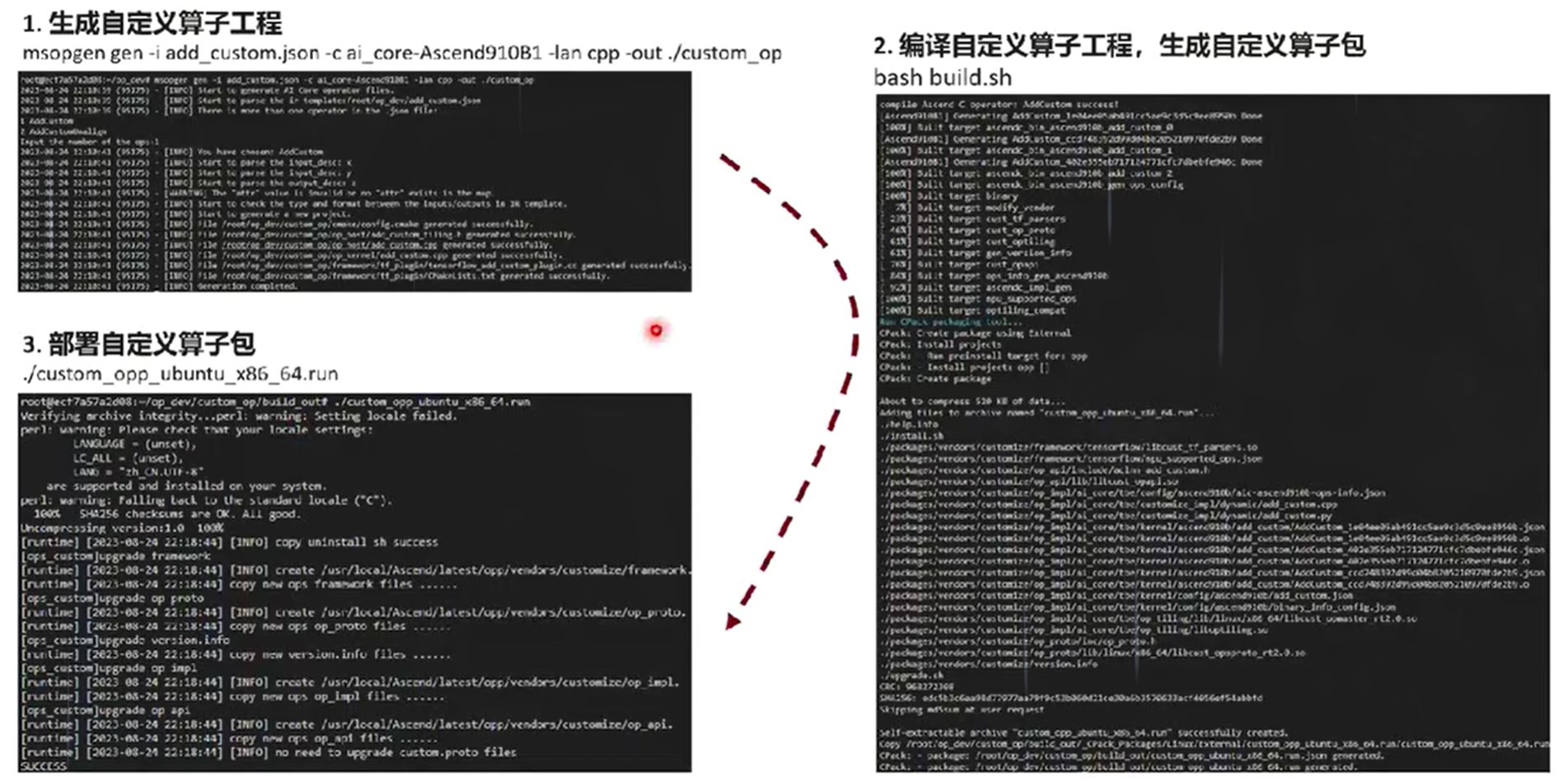
2. 创建
CV大法
3. 编译部署

样例演示
十一、算子调用
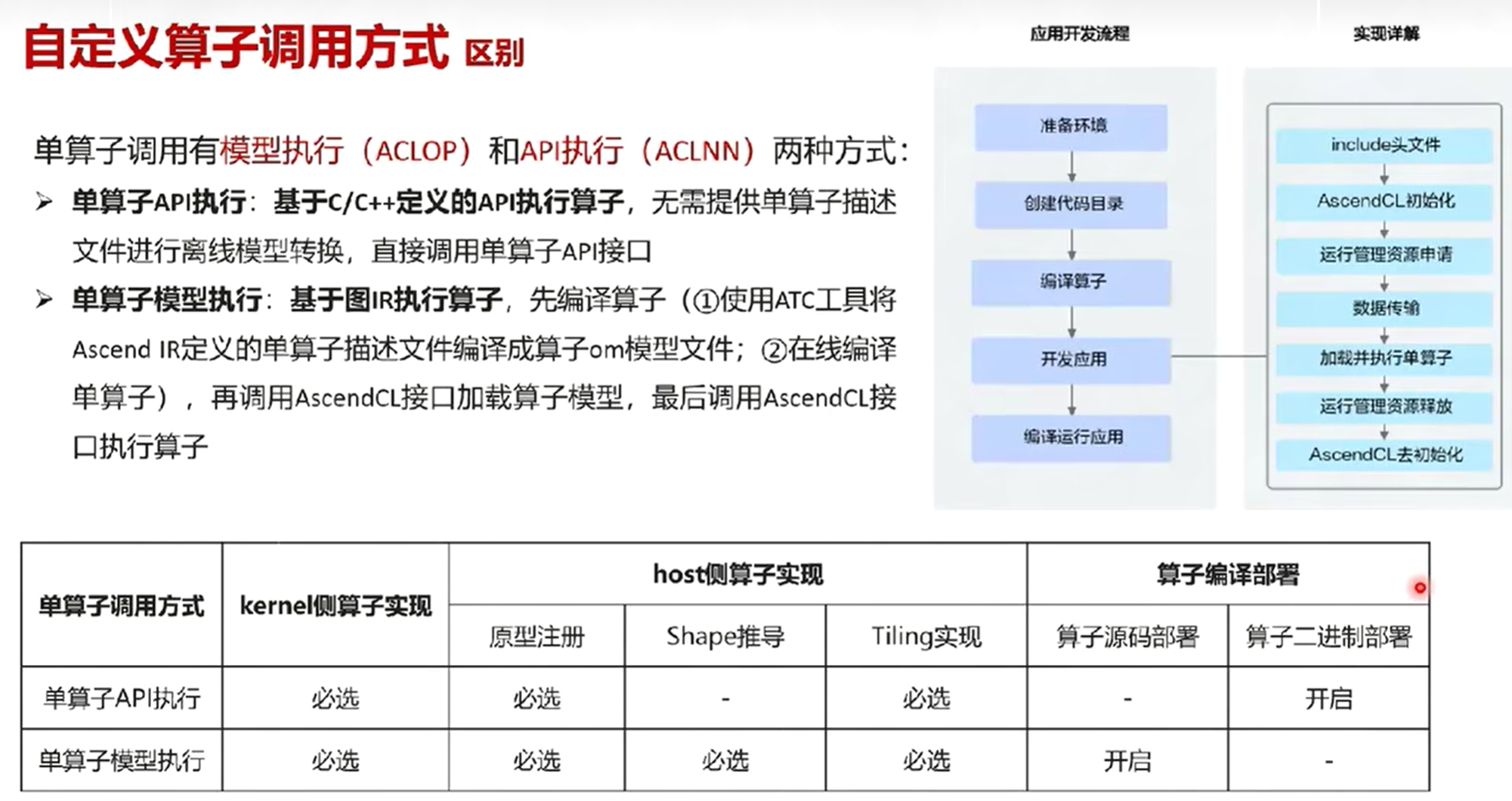
自定义算子调用方式
快速调用方式
- 需完成算子核函数的开发
- 基于内核调用符方式进行算子调用运行
标准调用方式
- 需完成算子交付件的开发
- 需完成应用程序的开发
- 基于单算子API(ACLNN)/单算子模型(ACLOP)/PyTorch Adapter等方式进行算子调用运行
| 快速开发流程与调用方式 | 标准开发流程与调用方式 | |
|---|---|---|
| 代码文件 | 少 | 多 |
| 开发时间 | 短 | 长 |
| 使用场景 | 单算子调用,快速验证算法逻辑 | 单算子网络/整网部署使用 |
| 推荐开发顺序 | 先 | 后 |
单算子API调用方式(Aclnn)


单算子模型调用方式(Aclop)
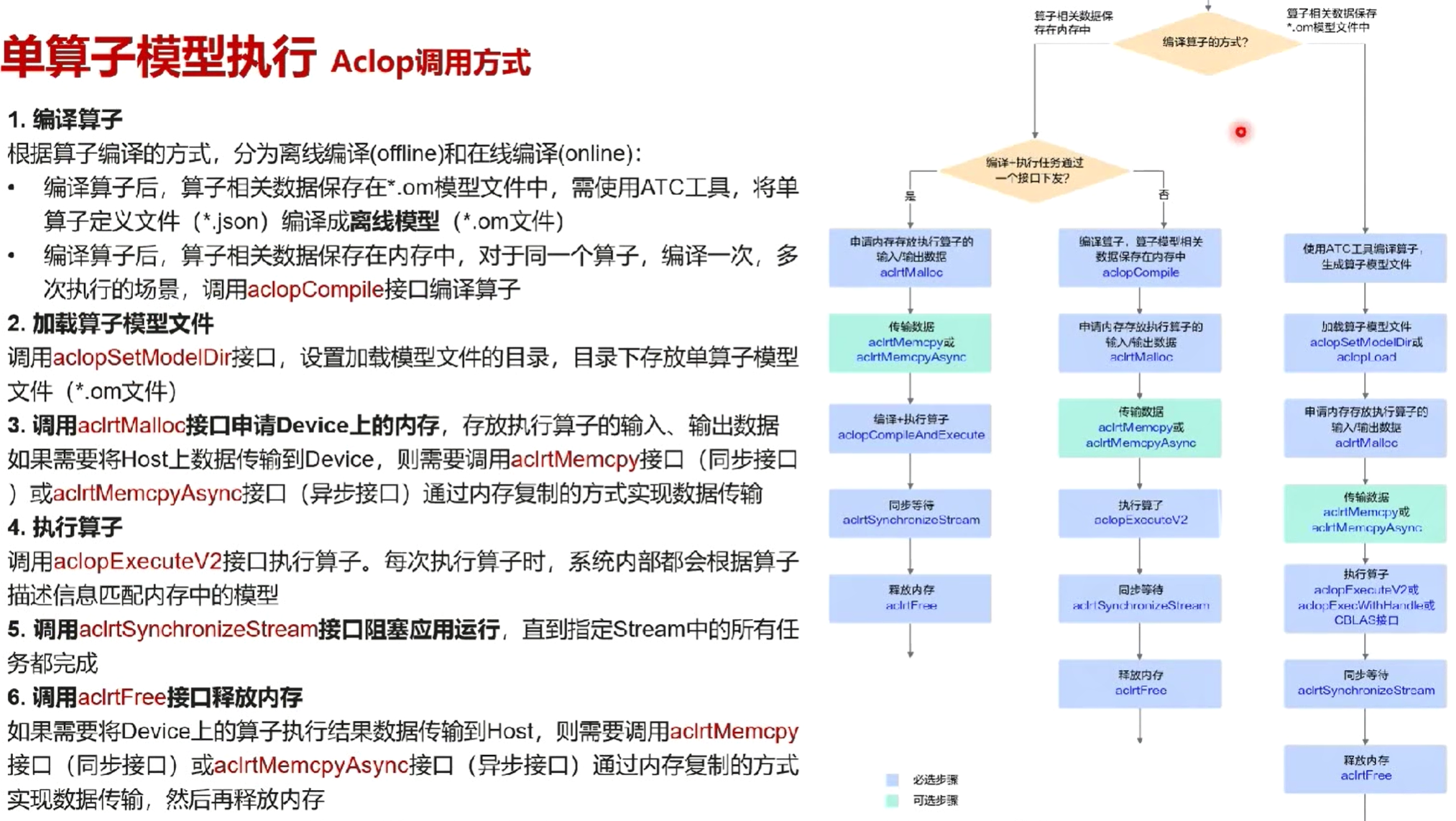
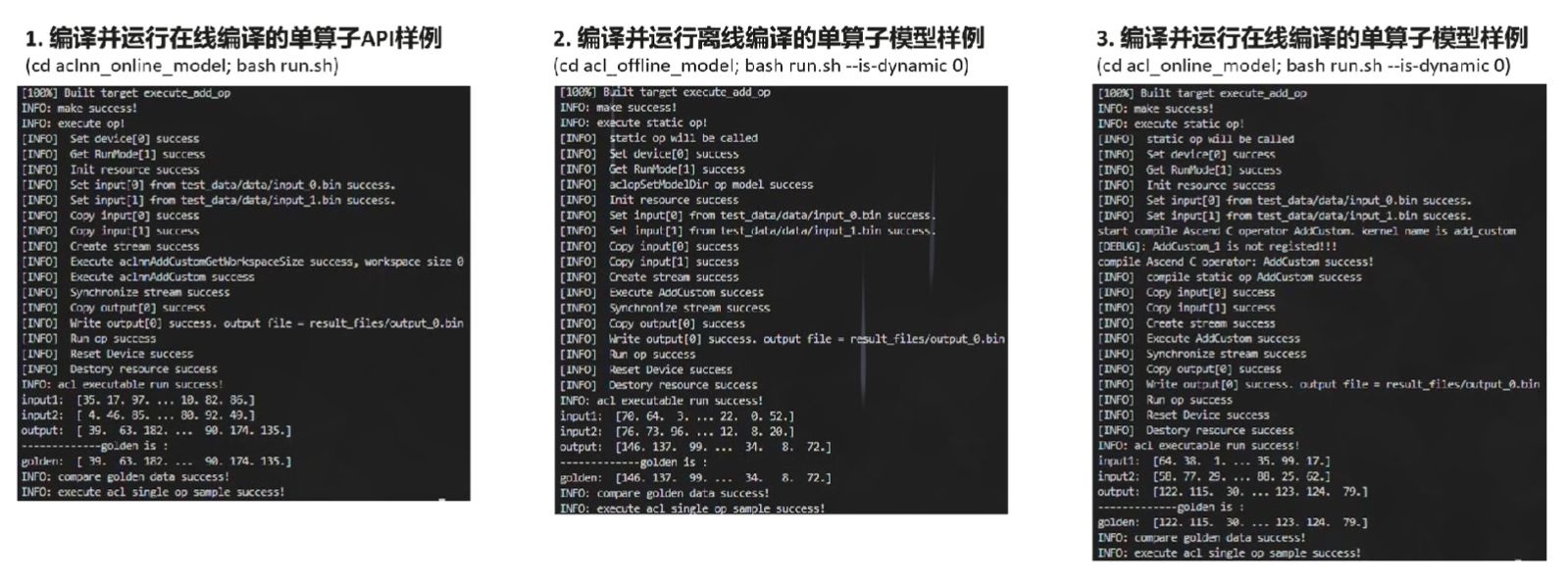
样例演示
编译算子工程
部署算子包
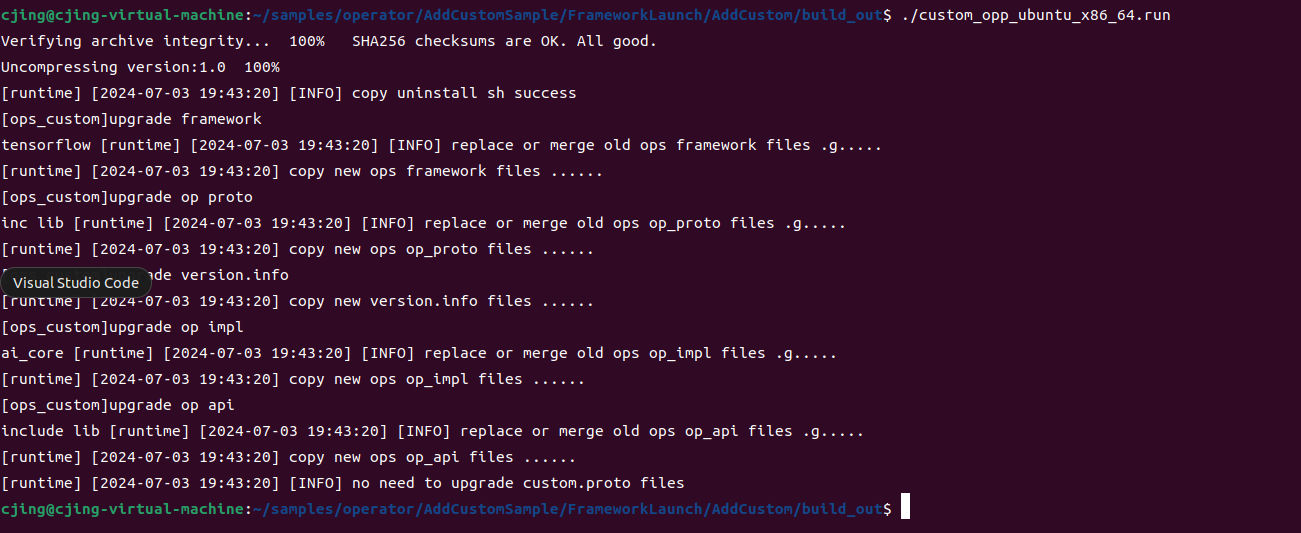
算子调用
单算子API调用
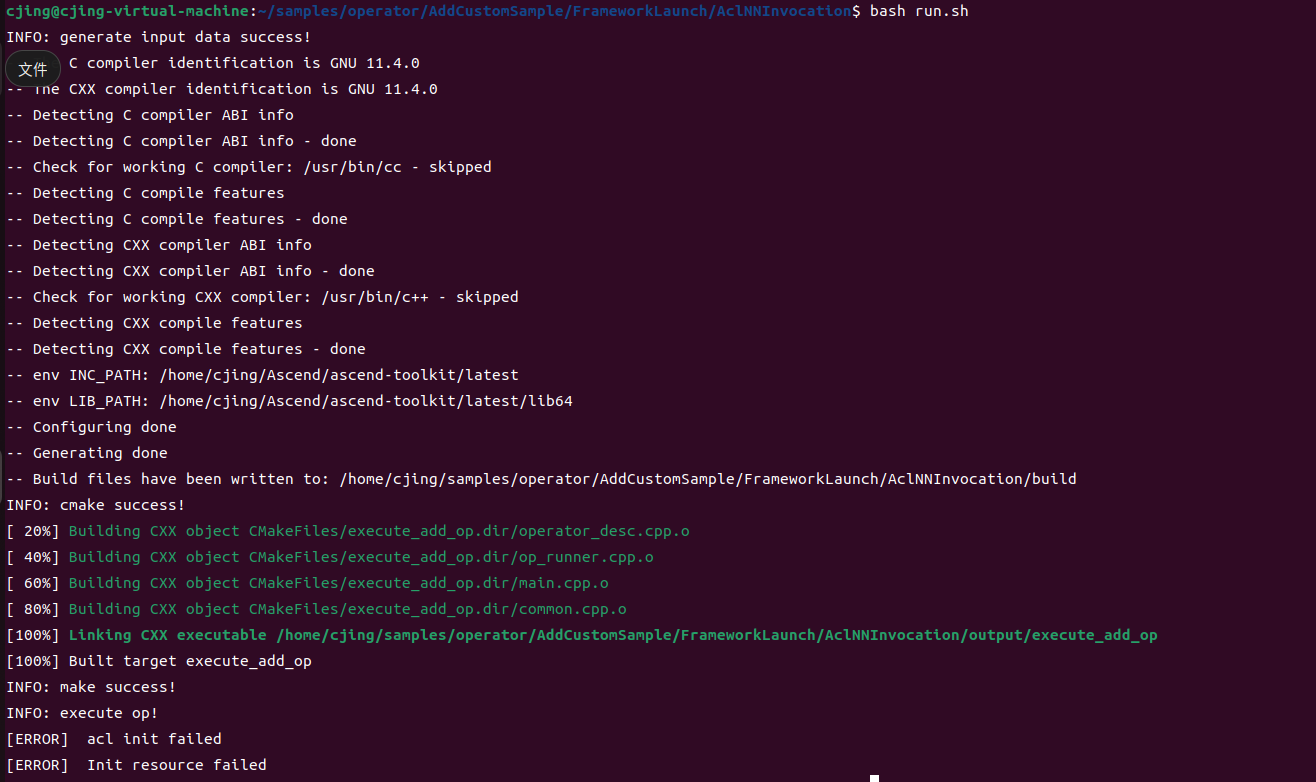
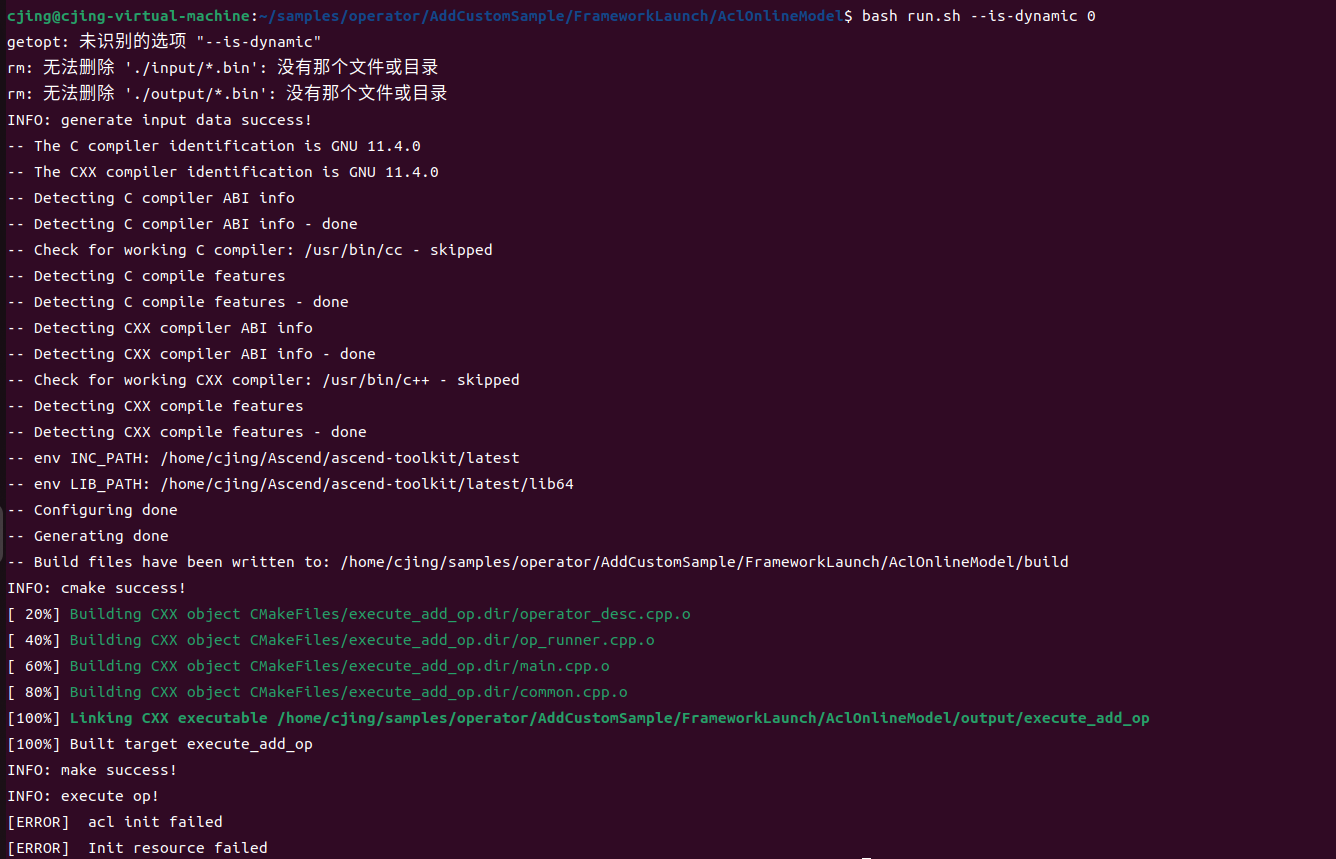
离线编译的单算子模型
在线编译的单算子模型
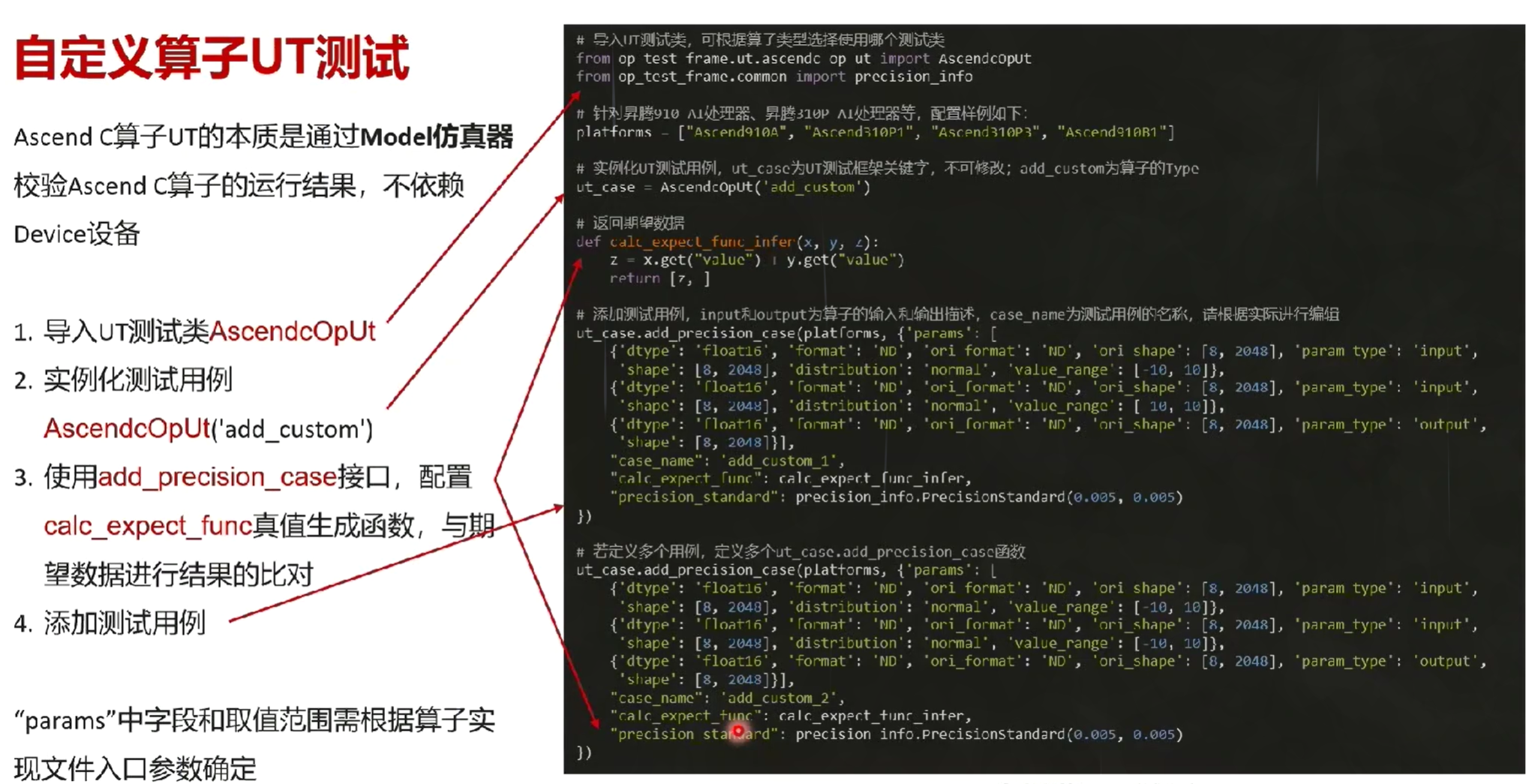
十二、算子测试

自定义算子UT测试
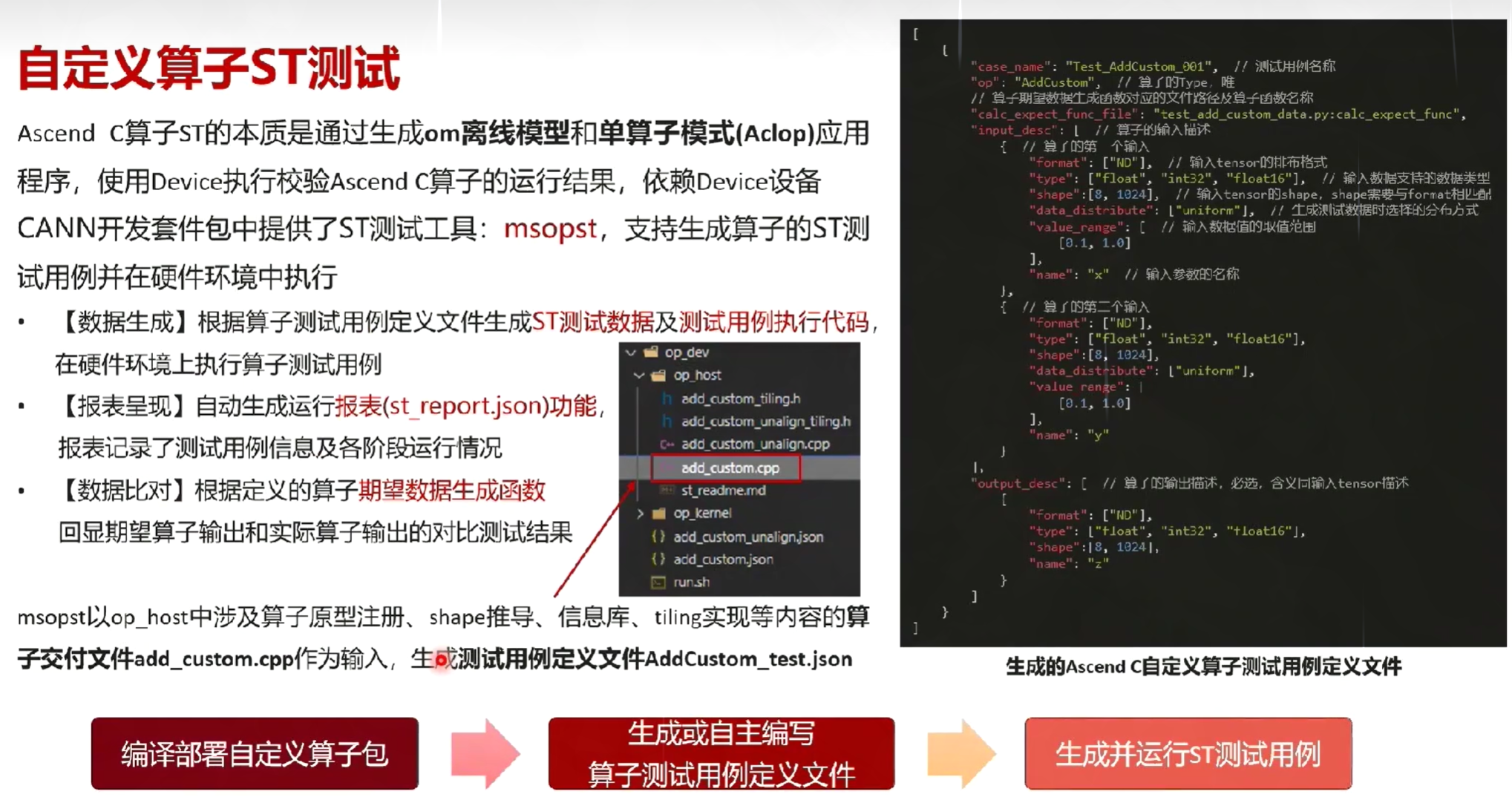
自定义算子ST测试
十三、PyTorch算子调试
十四、矩阵编程
基础知识
矩阵乘法概述
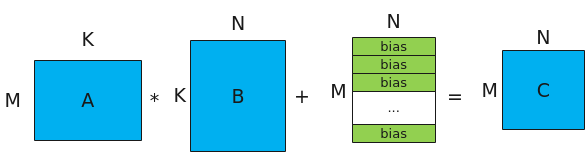
MatMul的计算公式为:C = A * B + bias,其示意图如下。
- A、B为源操作数,A为左矩阵,形状为[M, K];B为右矩阵,形状为[K, N]。
- C为目的操作数,存放矩阵乘结果的矩阵,形状为[M, N]。
- bias为矩阵乘偏置,形状为[1,N]。对A*B结果矩阵的每一行都采用该bias进行偏置。
矩阵乘法数据流
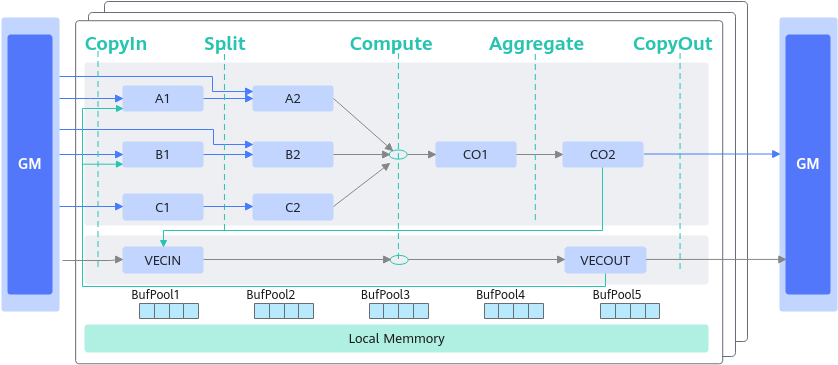
在了解矩阵乘法数据流之前,需要先回顾一下几个重要的存储逻辑位置的概念:
-
搬入数据的存放位置:A1,用于存放整块A矩阵,可类比CPU多级缓存中的二级缓存;
-
搬入数据的存放位置:B1,用于存放整块B矩阵,可类比CPU多级缓存中的二级缓存;
-
搬入数据的存放位置:A2,用于存放切分后的小块A矩阵,可类比CPU多级缓存中的一级缓存;
-
搬入数据的存放位置:B2,用于存放切分后的小块B矩阵,可类比CPU多级缓存中的一级缓存;
-
结果数据的存放位置:CO1,用于存放小块结果C矩阵,可理解为Cube Out;
-
结果数据的存放位置:CO2,用于存放整块结果C矩阵,可理解为Cube Out;
-
搬入数据的存放位置:VECCALC,一般在计算需要临时变量时使用此位置。
矩阵乘法数据流指矩阵乘的输入输出在各存储位置间的流向。逻辑位置的数据流向如下图所示(为了简化描述,没有列出bias): -
A矩阵从输入位置到A2的数据流如下(输入位置可以是GM或者VECOUT):GM->A2,GM->A1->A2;VECOUT->A1->A2。
-
B矩阵从输入位置到B2的数据流如下(输入位置可以是GM或者VECOUT):GM->B2,GM->B1->B2;VECOUT->B1->B2。
-
完成A2*B2=CO1计算。
-
CO1数据汇聚到CO2:CO1->CO2。
-
从CO2到输出位置(输出位置可以是GM或者VECIN):CO2->GM/CO2->VECIN。
数据格式
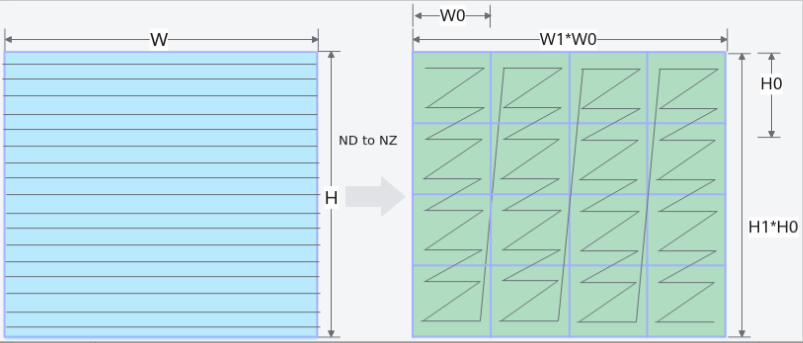
- 普通格式ND:N维张量
- 特殊格式NZ(增加矩阵乘的运算速度):为满足AICore中Cube计算单元高性能计算的需要,引入该特殊格式。
ND –> NZ的变换过程为:
(..., N,H, W )->pad->(..., N, H1*H0, W1*W0)->reshape->(..., N, H1, H0, W1, W0)->transpose->(..., N, W1, H1, H0, W0)
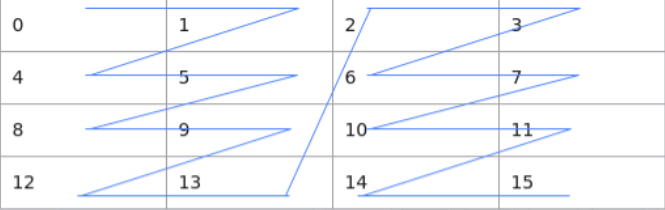
如下图所示 (W,H)大小的矩阵被分为(H1W1)个分形,按照column major排布,形状如N字形;每个分形内部有(H0W0)个元素,按照row major排布,形状如z字形。所以这种数据格式称为NZ(大N小Z)格式。
下面我们再通过一个具体的例子来深入理解ND和NZ格式的数据排布区别。假设分形格式为22,如下图所示44的矩阵,ND和NZ格式存储两种情况下,数据在内存中的排布格式分别为:
ND: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
NZ: 0, 1, 4, 5, 8, 9, 12, 13, 2, 3, 6, 7, 10, 11, 14, 15
TPosition
Ascend C管理不同层级的物理内存时,用一种抽象的逻辑位置(TPosition)来表达各级别的存储,代替了片上物理存储的概念,开发者无需感知硬件架构。
GM:ACore的外部存储
VECCALC:计算过程中中间变量的存储位置
TSCM
- 从L1上划分出一块内存,新增加了一个QuePosition类型TSCM。
- 用户可以提前将数据存放在TSCM中,在Matmul运算时可以减少搬运。
数据分块
-
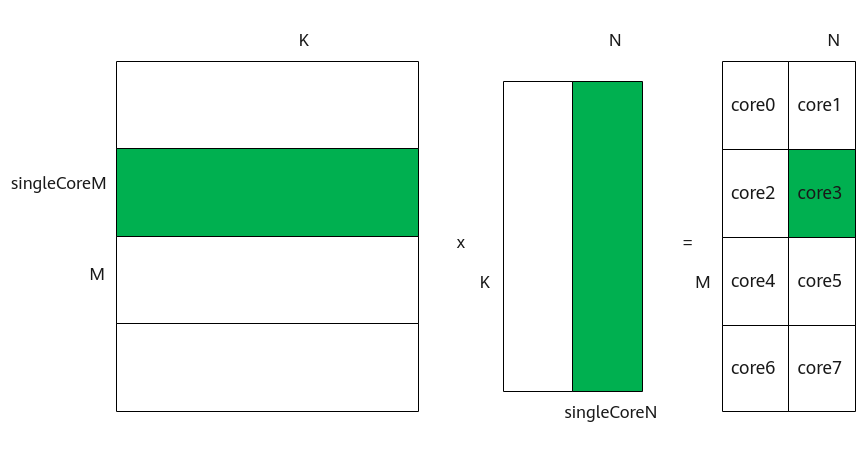
多核切分
为了实现多核并行,需要将矩阵数据进行切分,分配到不同的核上进行处理。切分策略如下图所示:- 对于A矩阵,沿着M轴进行切分,切分成多份的singleCoreM,单核上处理SingleCoreM * K大小的数据。
- 对于B矩阵,沿着N轴进行切分,切分成多份的singleCoreN,单核上处理K * SingleCoreN大小的数据。
- 对于C矩阵,SingleCoreM * K大小的A矩阵和K * SingleCoreN大小的B矩阵相乘得到SingleCoreM * SingleCoreN大小的C矩阵,即为单核上输出的C矩阵大小。
比如,下图中共有8个核参与计算,将A矩阵沿着M轴划分为4块,将B矩阵沿着N轴切分为两块,单核上仅处理某一分块(比如图中绿色部分为core3上参与计算的数据):SingleCoreM * K大小的A矩阵分块和SingleCoreN* K大小的B矩阵分块相乘得到SingleCoreM * SingleCoreN大小的C矩阵分块。
-
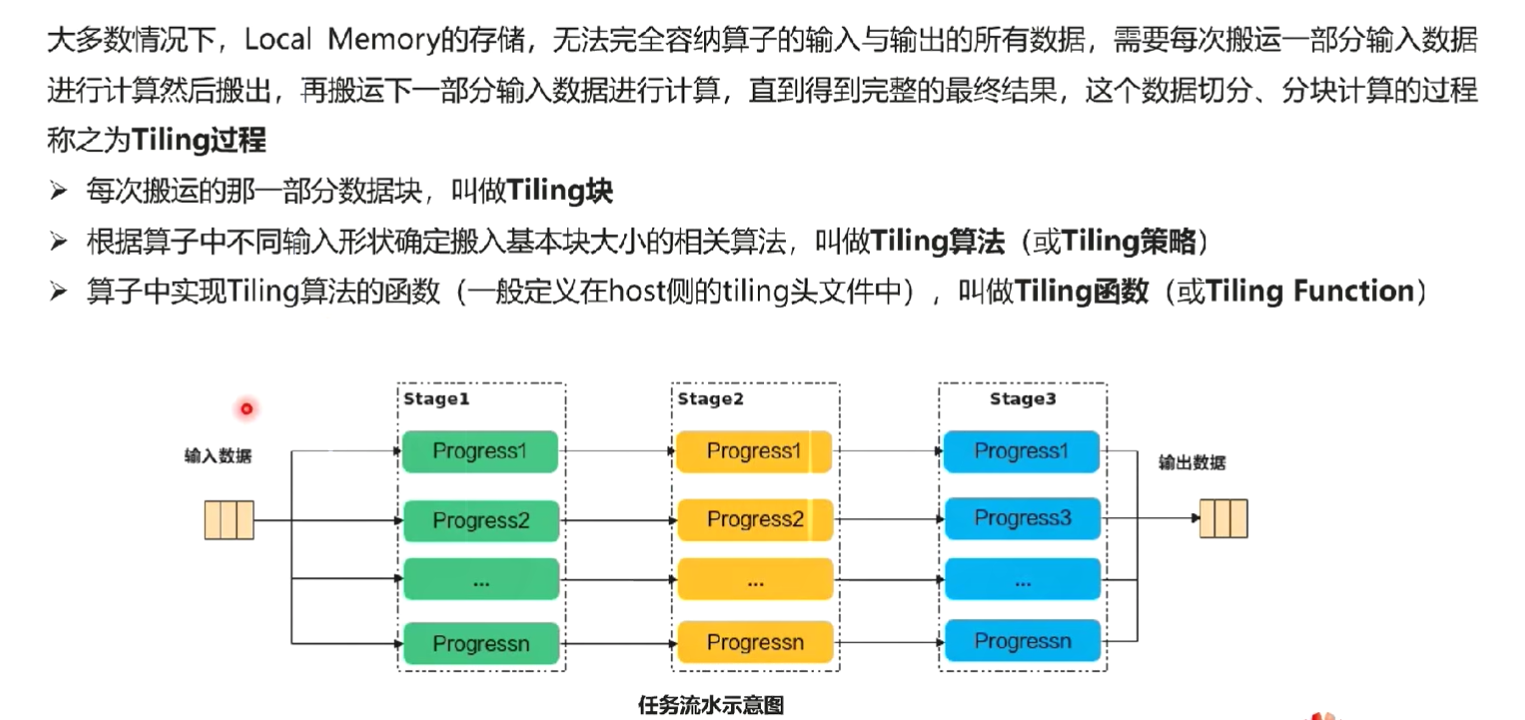
核内切分
大多数情况下,Local Memory的存储,无法完整的容纳算子的输入与输出,需要每次搬运一部分输入进行计算然后搬出,再搬运下一部分输入进行计算,直到得到完整的最终结果,也就是需要做核内的输入切分。切分的策略如下所示:-
对于A矩阵,沿M轴进行切分,切分成多份的\(baseM\);沿K轴进行切分,切分成多份的\(baseK\)。
-
对于B矩阵,沿N轴进行切分,切分成多份的\(baseN\),沿K轴进行切分,切分成多份的\(baseK\)。
-
对于C矩阵,A矩阵中\(baseM * baseK\)大小的分块和B矩阵中 \(baseK * base N\)大小的分块相乘并累加,得到C矩阵中对应位置\(baseM * base N\)大小的分块。比如,图中结果矩阵中的蓝色矩阵块5是通过如下的累加过程得到的:\(a*a+b*b+c*c+d*d+e*e+f*f\)。
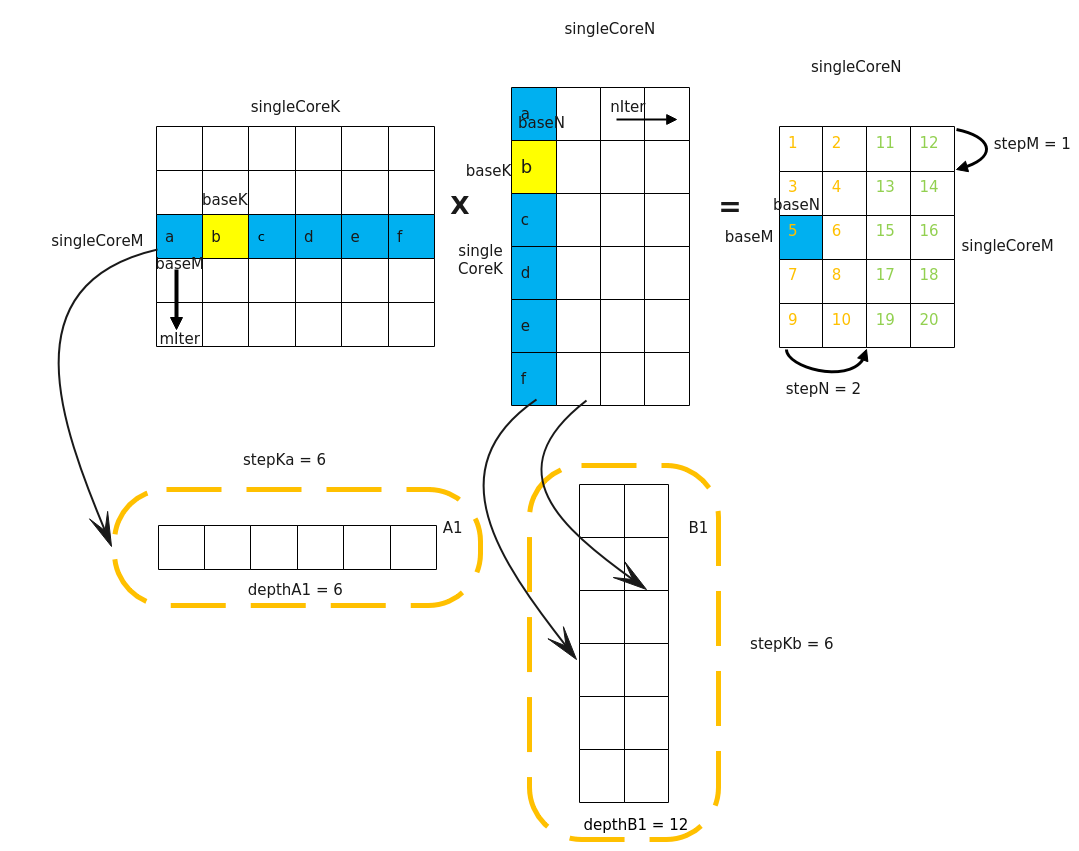
除了baseM, baseN, baseK外,还有一些常用的tiling参数,其含义如下: -
iterateOrder:一次Iterate迭代计算出[baseM, baseN]大小的C矩阵分片。Iterate完成后,Matmul会自动偏移下一次Iterate输出的C矩阵位置,iterOrder表示自动偏移的顺序。
- 0代表先往M轴方向偏移再往N轴方向偏移
- 1代表先往N轴方向偏移再往M轴方向偏移
-
depthA1,depthB1:A1、B1上存储的矩阵片全载A2/B2的份数,A2、B2存储大小分别是\(baseM * baseK\),\(baseN * baseK\)。
-
stepM,stepN:stepM为左矩阵在A1中缓存的bufferM方向上baseM的倍数。stepN为右矩阵在B1中缓存的bufferN方向上baseN的倍数。
-
stepKa,stepKb:stepKa为左矩阵在A1中缓存的buffer K方向上baseK的倍数,stepKb为右矩阵在B1中缓存的buffer K方向上baseK的倍数。
-
MatMul核函数开发
实现矩阵乘运算的具体步骤如下:
- 创建MatMul对象
- 初始化
- 设置左矩阵A、右矩阵B、Bias
- 完成矩阵乘操作
- 结束矩阵乘操作
// 1、创建MatMul对象
typedef MatmulType<TPosition:: GM,CubeFormat::ND,half> aType; //a矩阵内存逻辑位置为GM,数据格式为ND,数据类型为half
typedef MatmulType<TPosition:: GM,CubeFormat::ND,half> bType;
typedef MatmulType<TPosition:: GM,CubeFormat::ND,float> cType;
typedef MatmulType<TPosition:: GM,CubeFormat::ND,float> biasType;
Matmul<aType,bType,cType,biasType> mm;
mm.Init(&tiling,&tpipe); //初始化MatMul对象,传入tiling参数和tpipe对象
//2、设置左矩阵A、右矩阵B、Bias
mm.SetTensorA(gm_a); //设置矩阵乘的左矩阵A
mm.SetTensorB(gm_b); //设置矩阵乘的右矩阵B
mm.SetBias(gm_bias); //设置矩阵乘的Bias
//3、完成矩阵乘操作
while(mm.Iterate()){
mm.GetTensorC(gm_c);//配合Iterate使用,一次Iterate后,获取一块C矩阵片
}//每调用一次Iterate,会计算出一片baseM*baseN的C矩阵
//mm.IterateAll(gm_c); //调用IterateAll,会计算出singleCoreM*singleCoreN大小的C矩阵
//4、结束矩阵乘操作
mm.End();
十五、性能优化
算子计算流程优化
1.输入条件
- 芯片参数,包括通路带宽,buff大小,计算指令的cycle数数据
- 计算flops分析,计算的数据搬运量分析
2.分析过程
- 首先评估计算所需时间 tc
- 计算搬运数据所需时间 tb,通常包括tbln和tbOut ,比如VEC,但是如果是融合算子或者MM,则要计算
每个路径上的时间。 - Tc>tb,则计算bound,理论时间可以按照tc作为基准,通常可以要求算子达成tc*80%
- Tb>tc,则搬运bound,则可以考虑使用这个作为理论基准,通常可以要求算子达成tb*80%
3.注意事项
- 一个计算达成了某个执行单元的bound并不代表该算子已经达成了算子的性能可达上线;
- 如果是计算单元已经达成了bound,并且算法并没有重复计算过程,那么认为算子性能已经最优
- 如果搬运单元已经达成bound,并且算法已经达成了搬运量最小的算法,那么可以认为算子性能已经达成最优
- 部分bound是因为算法设计有问题,并没有找到搬运量最小算法来进行计算,而产生bound,这种情况通常出现在MM计算
tiling对性能的影响——影响系数-数倍的性能影响
硬件单元 Vector侧:UB Cube侧:L1和L0C
单核:核内流水并行,调tiling,减少循环次数
多核:多核切分数据
代码实现优化
API指令
Cache优化

层次化访存优化
Buffer优化措施

shape对齐亲和计算

计算资源利用优化
十六、个人见解
host侧tiling实现:core内部存储不够大,需要对输入数据进行切片,搬入搬出。
device侧kernel实现:
算子开发
常量介绍
TOTAL_LENGTH
USE_CORE_NUM
BLOCK_LENGTH
TILE_NUM:每个核上总计算数据分块个数
BUFFER_NUM:每个核上总计算数据大小
TILE_LENGTH:每个分块大小
1 矢量编程
1.1 算子实现
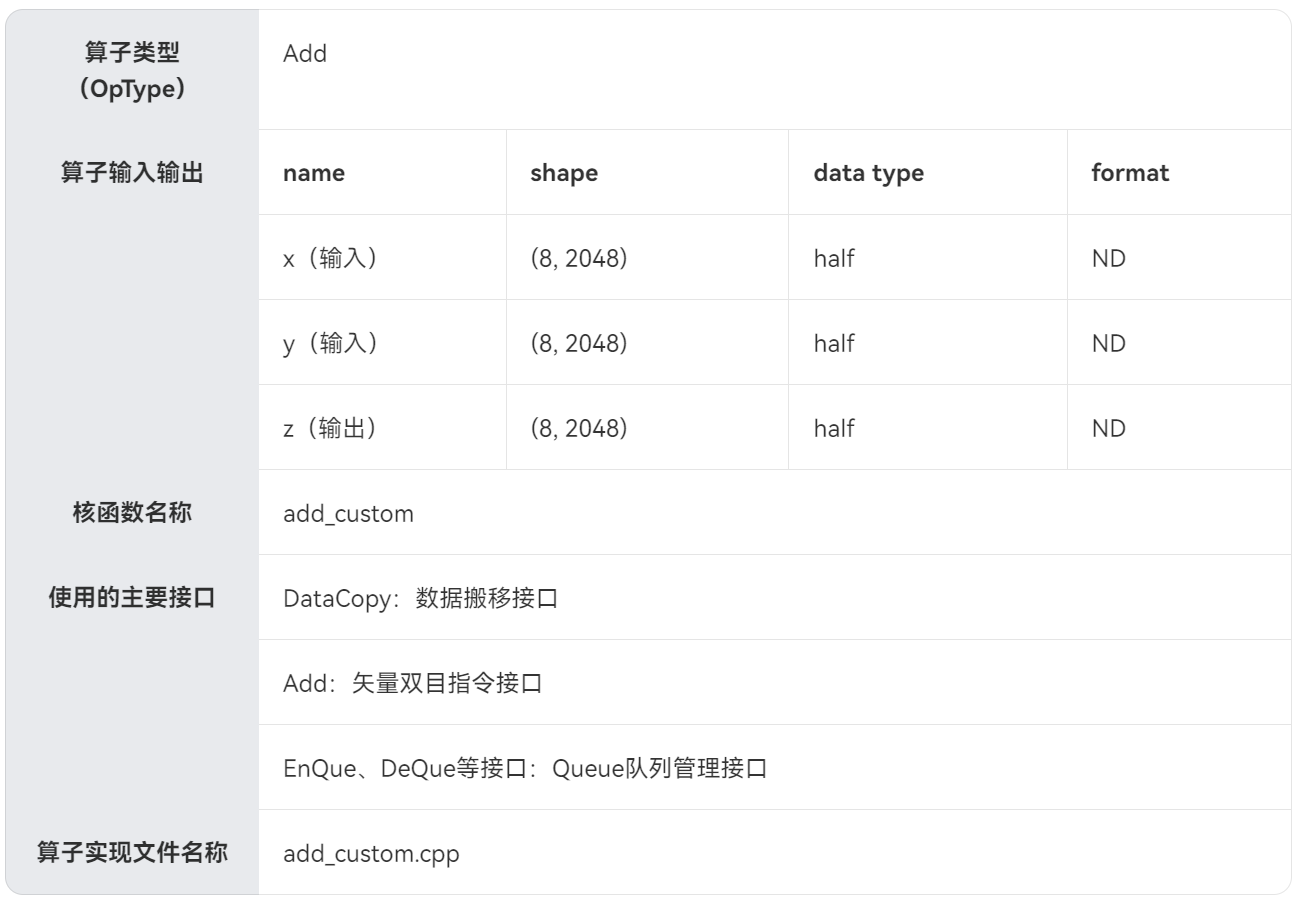
算子设计规格
核函数定义
extern "C" __global__ __aicore__ void add_custom(GM_ADDR x, GM_ADDR y, GM_ADDR z)
{
KernelAdd op;
op.Init(x, y, z); //完成内存初始化相关工作
op.Process(); //完成算子实现的核心逻辑
}
算子实现流程
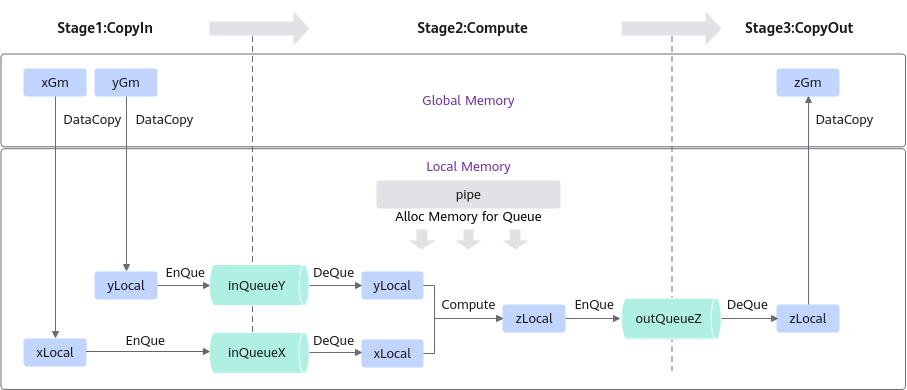
算子类中主要实现上述流程,包含对外开放的初始化Init函数和核心处理函数Process,Process函数中会对上图中的三个基本任务进行调用;同时包括一些算子实现中会用到的私有成员,比如上图中的Global Tensor和VECIN、VECOUT队列等。KernelAdd算子类具体成员如下:
class KernelAdd {
public:
constexpr int32_t TOTAL_LENGTH = 8 * 2048; // 数据整体长度
constexpr int32_t USE_CORE_NUM = 8; // 使用8个核
constexpr int32_t BLOCK_LENGTH = TOTAL_LENGTH / USE_CORE_NUM; // 每个核上处理的数据大小
constexpr int32_t TILE_NUM = 8; // split data into 8 tiles for each core
constexpr int32_t BUFFER_NUM = 2; // tensor num for each queue
constexpr int32_t TILE_LENGTH = BLOCK_LENGTH / TILE_NUM / BUFFER_NUM; // seperate to 2 parts, due to double buffer
__aicore__ inline KernelAdd() {}
// 初始化函数,完成内存初始化相关操作
__aicore__ inline void Init(GM_ADDR x, GM_ADDR y, GM_ADDR z)
{
// get start index for current core, core parallel
// 获取输入和输出在Global Memory上的内存偏移地址
xGm.SetGlobalBuffer((__gm__ half*)x + BLOCK_LENGTH * GetBlockIdx(), BLOCK_LENGTH);
yGm.SetGlobalBuffer((__gm__ half*)y + BLOCK_LENGTH * GetBlockIdx(), BLOCK_LENGTH);
zGm.SetGlobalBuffer((__gm__ half*)z + BLOCK_LENGTH * GetBlockIdx(), BLOCK_LENGTH);
// 通过Pipe内存管理对象为输入输出Queue分配内存,单位为Bytes
pipe.InitBuffer(inQueueX, BUFFER_NUM, TILE_LENGTH * sizeof(half));
pipe.InitBuffer(inQueueY, BUFFER_NUM, TILE_LENGTH * sizeof(half));
pipe.InitBuffer(outQueueZ, BUFFER_NUM, TILE_LENGTH * sizeof(half));
}
// 核心处理函数,实现算子逻辑,调用私有成员函数CopyIn、Compute、CopyOut完成矢量算子的三级流水操作
__aicore__ inline void Process()
{
// loop count need to be doubled, due to double buffer
constexpr int32_t loopCount = TILE_NUM * BUFFER_NUM;
// tiling strategy, pipeline parallel
for (int32_t i = 0; i < loopCount; i++) {
CopyIn(i);
Compute(i);
CopyOut(i);
}
}
private:
// 搬入函数,完成CopyIn阶段的处理,被核心Process函数调用
// a.使用DataCopy接口将GlobalTensor数据拷贝到LocalTensor
// b.使用EnQue将LocalTensor放入VecIn的Queue中
__aicore__ inline void CopyIn(int32_t progress)
{
// alloc tensor from queue memory
LocalTensor<half> xLocal = inQueueX.AllocTensor<half>();
LocalTensor<half> yLocal = inQueueY.AllocTensor<half>();
// copy progress_th tile from global tensor to local tensor
DataCopy(xLocal, xGm[progress * TILE_LENGTH], TILE_LENGTH);
DataCopy(yLocal, yGm[progress * TILE_LENGTH], TILE_LENGTH);
// enque input tensors to VECIN queue
inQueueX.EnQue(xLocal);
inQueueY.EnQue(yLocal);
}
// 计算函数,完成Compute阶段的处理,被核心Process函数调用
// a.使用DeQue从VecIn中取出LocalTensor
// b.使用Ascend C接口Add完成矢量计算
// c.使用EnQue将计算结果LocalTensor放入到VecOut的Queue中
// d.使用FreeTensor释放不再使用的LocalTensor
__aicore__ inline void Compute(int32_t progress)
{
// deque input tensors from VECIN queue
LocalTensor<half> xLocal = inQueueX.DeQue<half>();
LocalTensor<half> yLocal = inQueueY.DeQue<half>();
LocalTensor<half> zLocal = outQueueZ.AllocTensor<half>();
// call Add instr for computation
Add(zLocal, xLocal, yLocal, TILE_LENGTH);
// enque the output tensor to VECOUT queue
outQueueZ.EnQue<half>(zLocal);
// free input tensors for reuse
inQueueX.FreeTensor(xLocal);
inQueueY.FreeTensor(yLocal);
}
// 搬出函数,完成CopyOut阶段的处理,被核心Process函数调用
// a.使用DeQue接口从VecOut的Queue中取出LocalTensor
// b.使用DataCopy接口将LocalTensor拷贝到GlobalTensor上
// c.使用FreeTensor将不再使用的LocalTensor进行回收
__aicore__ inline void CopyOut(int32_t progress)
{
// deque output tensor from VECOUT queue
LocalTensor<half> zLocal = outQueueZ.DeQue<half>();
// copy progress_th tile from local tensor to global tensor
DataCopy(zGm[progress * TILE_LENGTH], zLocal, TILE_LENGTH);
// free output tensor for reuse
outQueueZ.FreeTensor(zLocal);
}
private:
TPipe pipe; //Pipe内存管理对象
TQue<QuePosition::VECIN, BUFFER_NUM> inQueueX, inQueueY; //输入数据Queue队列管理对象,QuePosition为VECIN
TQue<QuePosition::VECOUT, BUFFER_NUM> outQueueZ; //输出数据Queue队列管理对象,QuePosition为VECOUT
GlobalTensor<half> xGm, yGm, zGm; //管理输入输出Global Memory内存地址的对象,其中xGm, yGm为输入,zGm为输出
};
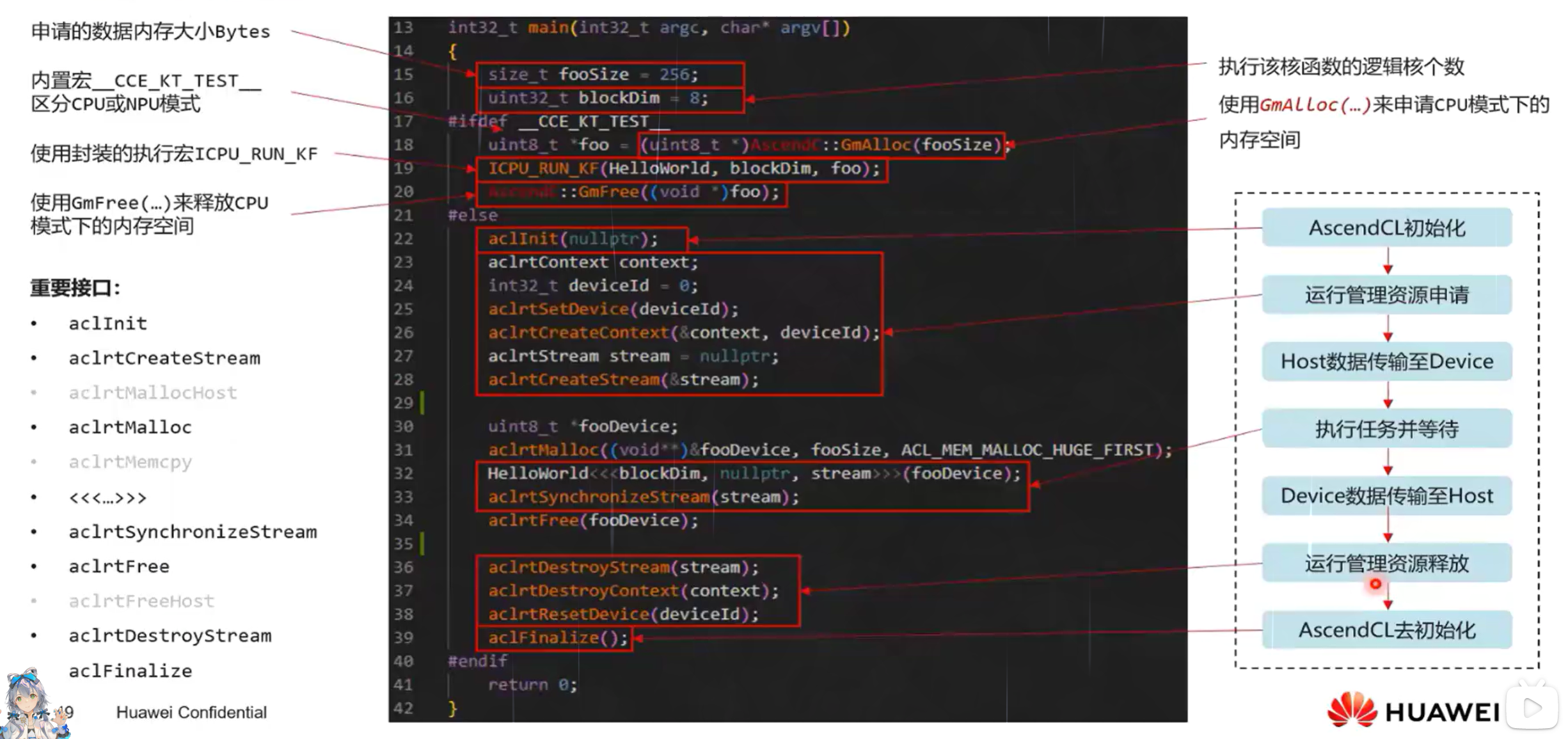
运行验证
核函数即算子kernel程序开发完成后,即可编写host侧的核函数调用程序,实现从host侧的APP程序调用算子,进行运行验证。包括CPU侧和NPU侧两种运行验证方法:
- CPU侧运行验证主要通过ICPU_RUN_KF CPU调测宏等CPU调测库提供的接口来完成;
- NPU侧运行验证主要通过使用<<<>>>内核调用符和AscendCL API提供的运行时接口来完成。
1.2 更多场景
1.2.1 固定shape场景
constexpr int32_t TOTAL_LENGTH = 8 * 2048; // total length of data
constexpr int32_t USE_CORE_NUM = 8; // num of core used
constexpr int32_t BLOCK_LENGTH = TOTAL_LENGTH / USE_CORE_NUM; // length computed of each core
constexpr int32_t TILE_NUM = 8; // split data into 8 tiles for each core
constexpr int32_t BUFFER_NUM = 2; // tensor num for each queue
constexpr int32_t TILE_LENGTH = BLOCK_LENGTH / TILE_NUM / BUFFER_NUM; // each tile length is seperated to 2 part, due to double buffer
1.2.2 动态shape场景
将上述代码转换为动态shape,需要在核函数定义中增加Tiling参数,在host侧计算Tiling参数并传入,然后基于Tiling参数计算得到singleCoreSize(每个核上总计算数据大小)、tileNum(每个核上总计算数据分块个数)、tileLength(每个分块大小)等变量。
__aicore__ inline void Init(GM_ADDR x, GM_ADDR y, GM_ADDR z, uint32_t totalLength, uint32_t tileNum)
{
ASSERT(GetBlockNum() != 0 && "block dim can not be zero!");
this->blockLength = totalLength / GetBlockNum();
this->tileNum = tileNum;
ASSERT(tileNum != 0 && "tile num can not be zero!");
this->tileLength = this->blockLength / tileNum / BUFFER_NUM;
// ...
}
extern "C" __global__ __aicore__ void add_custom(GM_ADDR x, GM_ADDR y, GM_ADDR z, GM_ADDR workspace, AddCustomTilingData tiling)
{
KernelAdd op;
op.Init(x, y, z, tiling.totalLength, tiling.tileNum);
op.Process();
}
1.2.3 shape非对齐场景
2 矩阵编程
3 融合算子编程
4 算子开发工程



success!

