考点总结
数字图像处理:利用计算机对图像进行去除噪声、增强、复原、分割、提取特征等的理论、方法和技术
基础知识
图像的分类
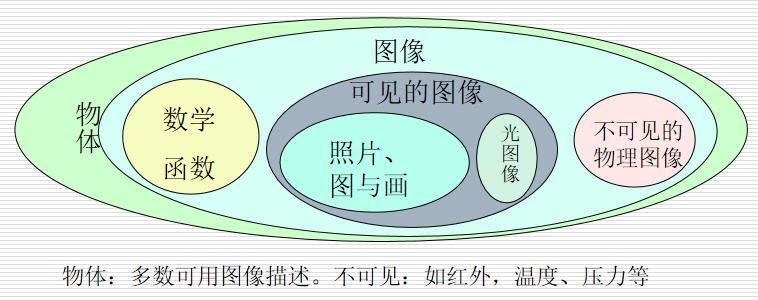
(1)从视觉特点,分为可见图像和不可见图像。
(2)从图像空间坐标和明暗程度的连续性,可分为模拟图像和数字图像。
分辨率
决定了图像的清晰度
分类:显示分辨率、图像分辨率
当显示分辨率大于图像分辨率时,会产生图像模糊的情况
当图像分辨率大于显示分辨率时,则只能显出图像的一部分
图像文件格式

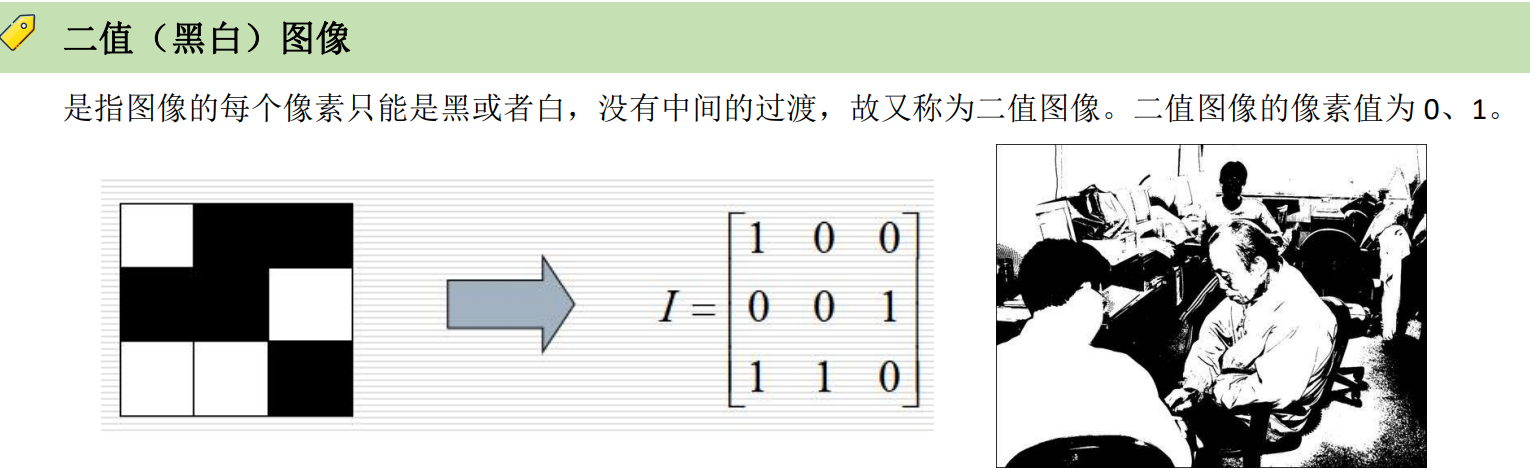
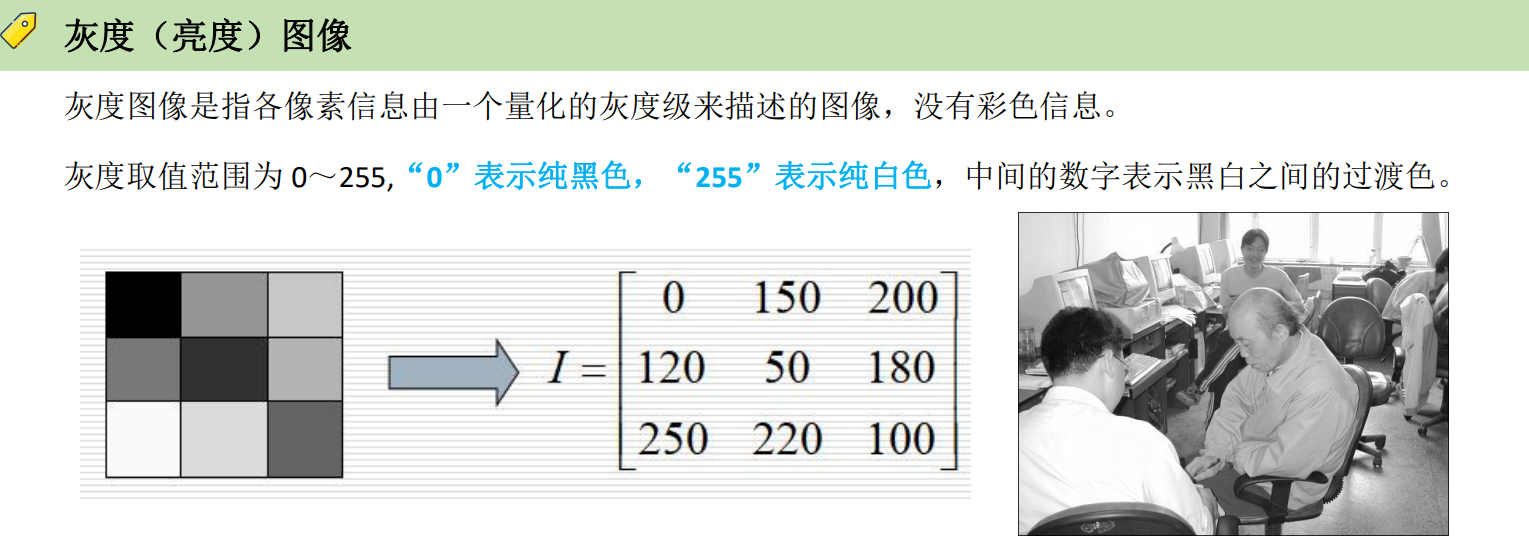
数字图像的基本类型

位图是通过许多像素点表示一幅图像,每个像素具有颜色属性和位置属性。位图分成如下 4 种:


数字图像处理的研究内容
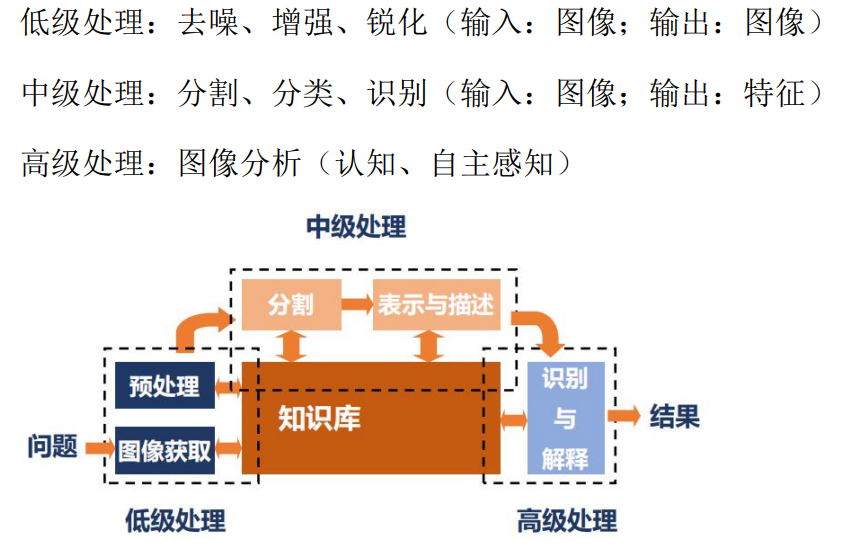
- 图像获取、表示和描述
- 原理:通过对图像中感兴趣的特征的定性和定量描述,从而赋予识别出的目标以符号标识和解释即将模拟图像信号转化为计算机所能接受的数字形式,以及将数字图像显示和表现出来(如打印)。这一过程包括摄取图像、光电转换、数字化
- 目的:
- 特点:
- 图像分析
- 原理:对图像中的不同对象进行分割、 特征提取和表示,从而有利于计算机对图像进行分类、 识别和理解。
- 目的:
- 特点:
- 图像复原
- 原理:
- 目的:
- 特点:
- 图像增强
- 原理:
- 目的:
- 特点:
- 图像重建
- 原理:
- 目的:
- 特点:
- 图像压缩编码
- 原理:
- 目的:①减少数据存储量;②降低数据率以减少传输带宽;③压缩信息量, 便于特征提取,为后续识别作准备。
- 特点:①充分考虑人的视觉特性; ②恰当地考虑对图像信号的分解与表述;③采用图像的合成与识别方案压缩数据。
- 图像变换
- 原理:
- 目的:简化图像处理过程和提高图像处理效果的基本技术
- 特点:傅里叶变换、 离散余弦变换和小波变换等
- 彩色图像处理
- 原理:
- 目的:
- 特点:
- 图像分割
- 原理:把一幅图像划分成背景和目标,从而提取感兴趣的目标来
- 目的:
- 特点:
数字图像处理的应用
- 医学应用:通过 CT 及核磁共振、超声波、 X 射线成像的分析等,可提供医学诊断依据。
- 气象预报:获取气象云图进行测绘、判读等
- 地球资源勘探
- 遥感:农、林等资源的调查,农作物长势监测,自然灾害监测、预报,地势、地貌测绘以及地质构造解译、找矿,环境污染检测等等。
- SPOT 图像用于监测土地变化
- 卫星影像用于土地动态监测
- 空间探索
- 工业生产:无损探伤,石油勘探,生产过程自动化(识别零件,装配质量检查),工业机器人研制等
- 军事:航空及卫星侦察照片的测绘、判读, 雷达、 声纳图像处理,导弹制导,军事仿真等
- 通信:图像传真,数字电视、网络可视聊天、可视电话网页动画等
- 生物特征识别
- 公安:指纹识别,印签、伪钞识别,安检,手迹、印记鉴别分析等
- 计算机合成图像
- 广告设计
- 计算机绘图
review

图像的统计特征
一维

多维

图像质量评价

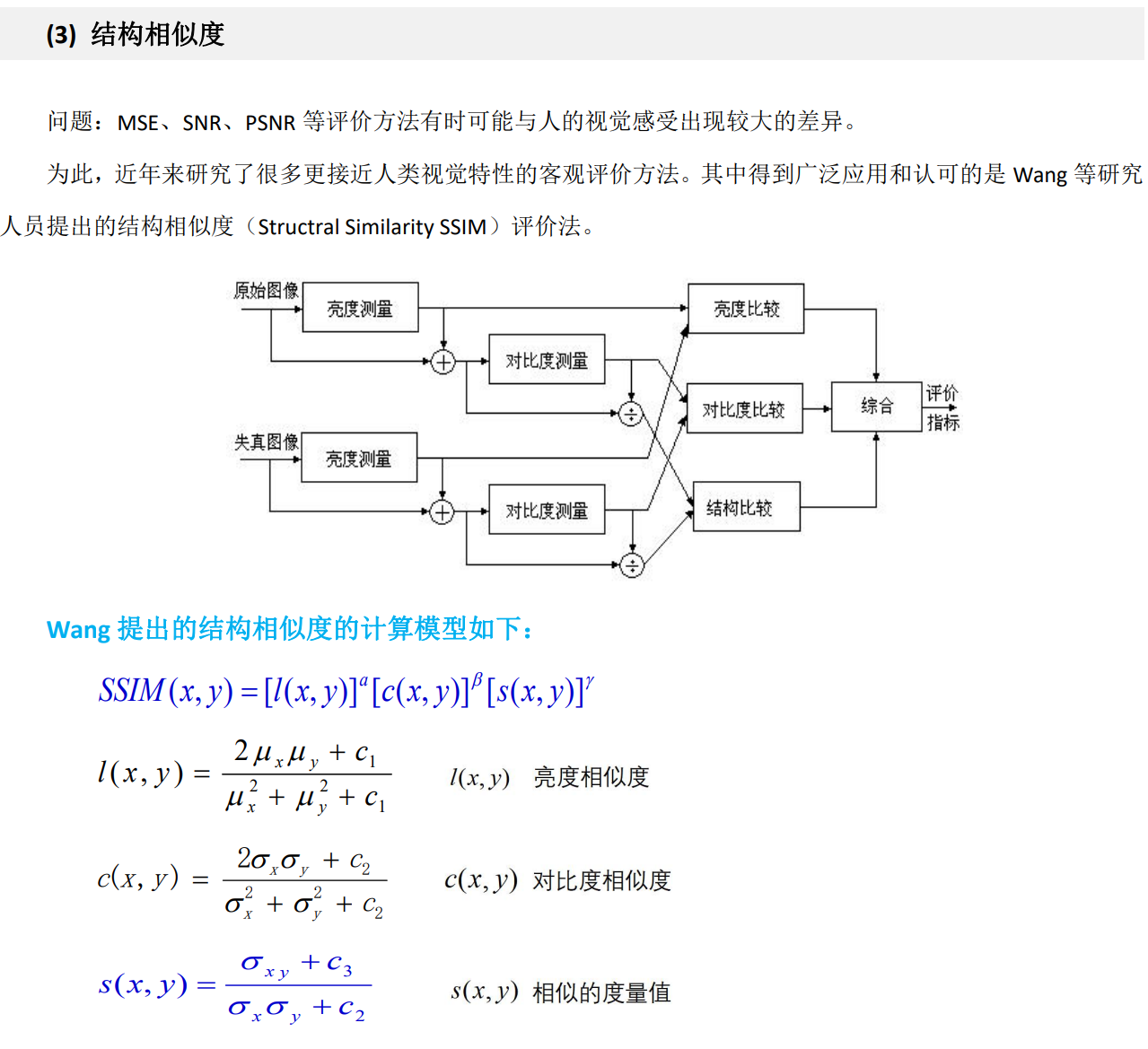

一、图的基本运算
1 数学基础
1.1 线性系统
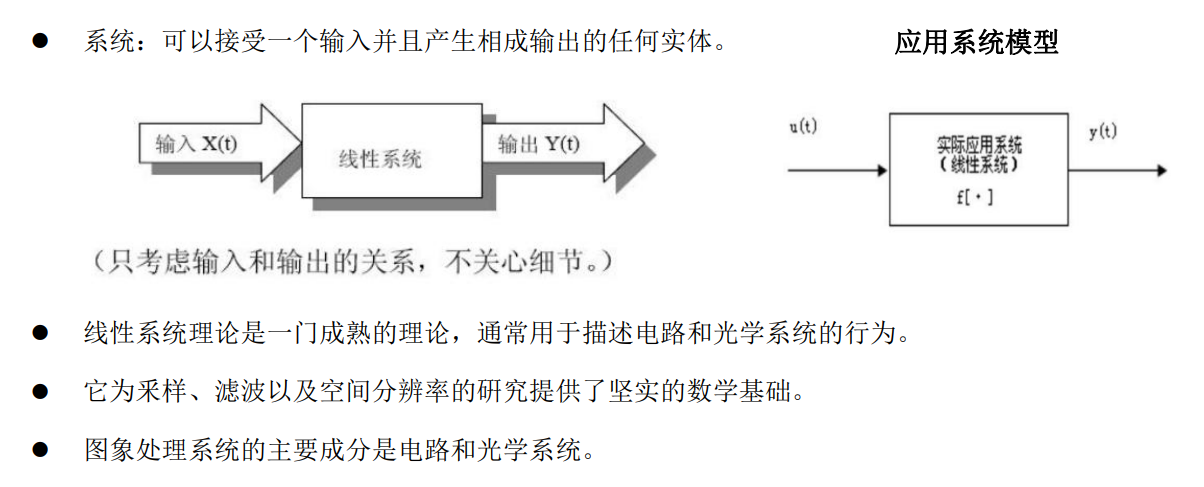
特性:

- 对于移不变系统,平移输入信号仅使输岀信号移动同样长度。重要的是输出信号的性质不变。
- 若输入图像相对于其原点有一平移,则输出图像除了相同的平移外其他不变。
1.2 调谐信号分析


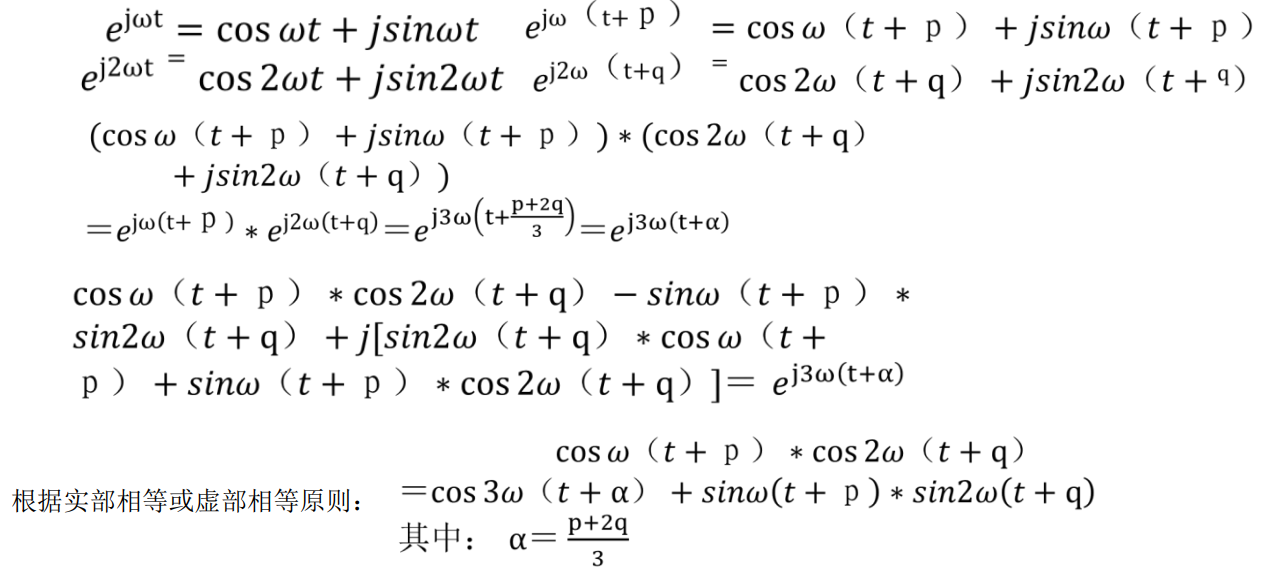


1.3 卷积和滤波
连续卷积
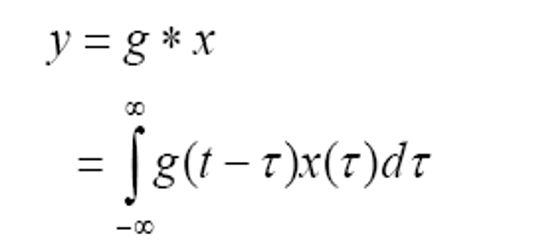 其中*用来表示两个函数的卷积
其中*用来表示两个函数的卷积
卷积运算的性质
- 交换性
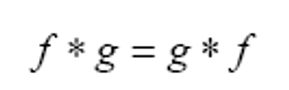
- 加法分配律
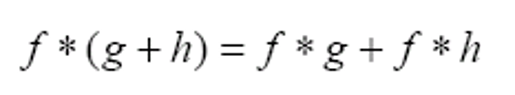
- 结合律
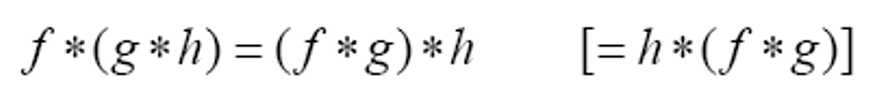
- 求导法则
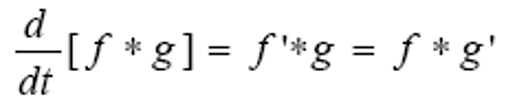
离散卷积
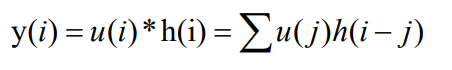
滤波
数学上的卷积运算在信号处理和图像处理学科上称为滤波

1.4 相关函数
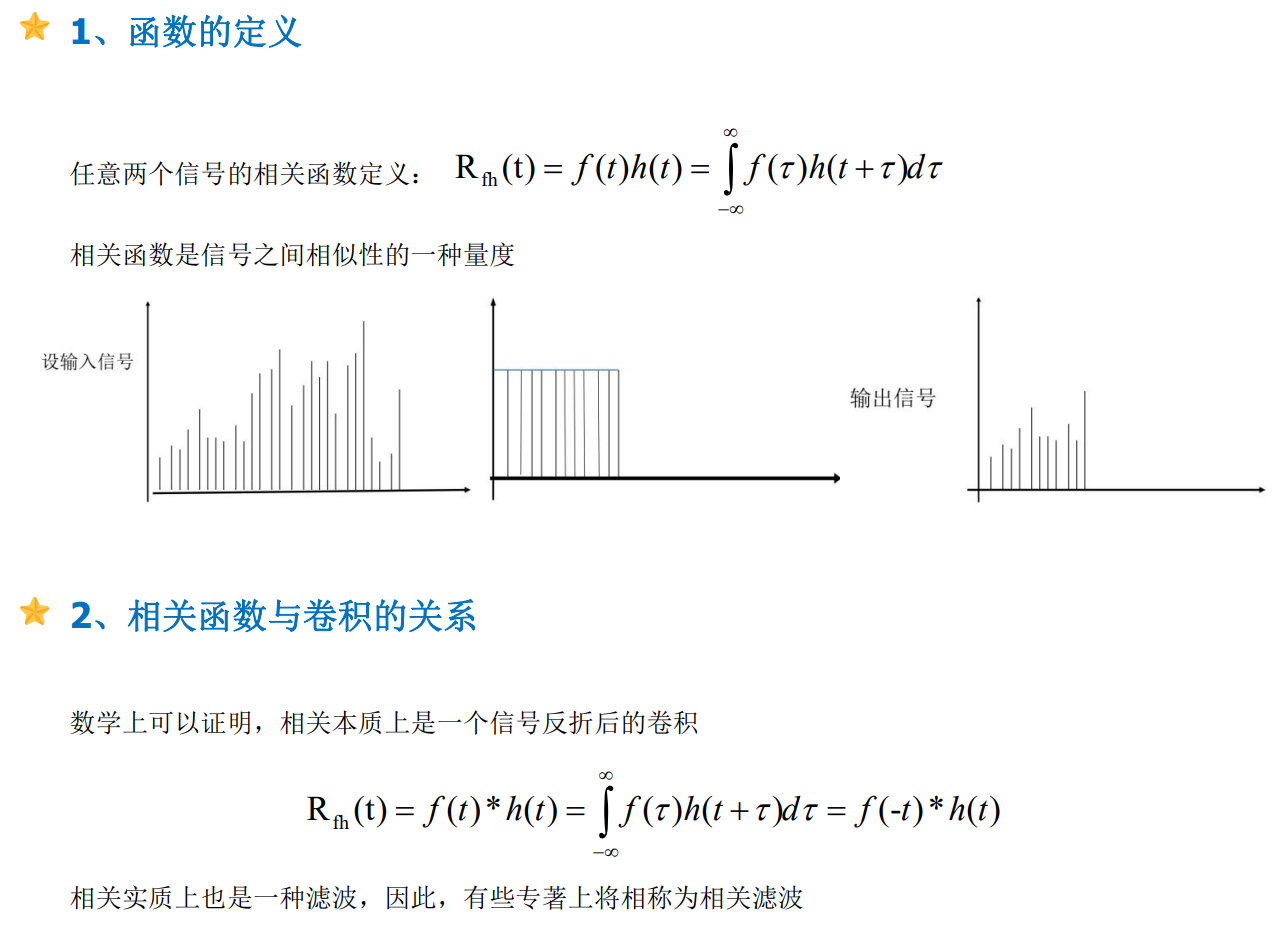
1.5 二维系统


2 基本运算类型

- 点运算:是指对一幅图像中每个像素点的灰度值进行计算的方法。
- 代数运算:是指将两幅或多幅图像通过对应像素之间的加、减、乘、除运算得到输出图像的方法。
- 逻辑运算:是指将两幅或多幅图像通过对应像素之间的逻辑与、或、非运算得到输出图像的方法。
- 几何运算:改变图像中物体对象(像素)之间的空间关系。
3 几何运算

几何变换可能改变图像中各物体之间的空间位置关系。
几何变换不改变像素值,而可能改变像素所在的位置。
1. 齐次坐标

2. 图像的平移

3. 图像的缩小
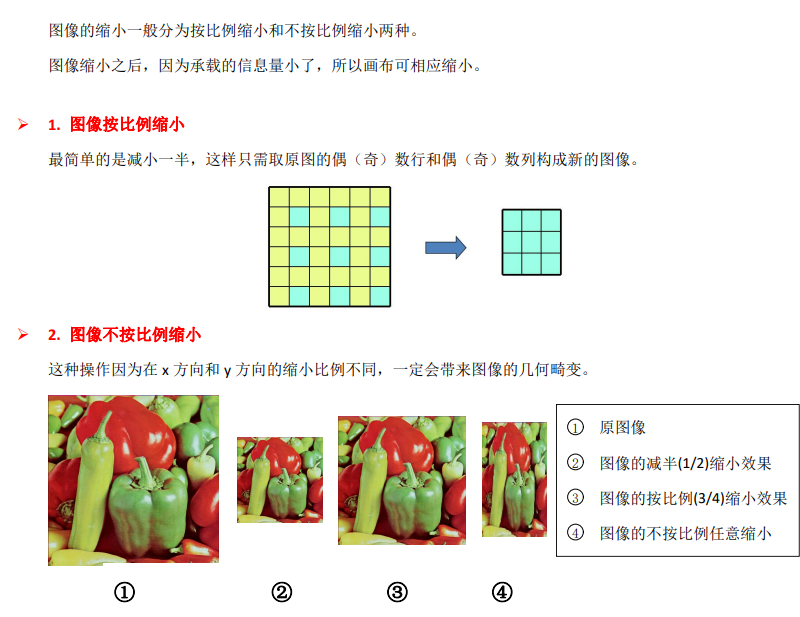
4. 图像的放大

5. 图像的镜像
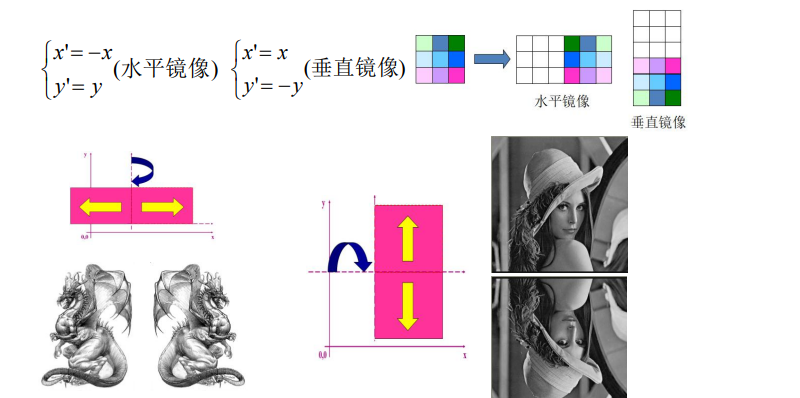
6. 图像的旋转
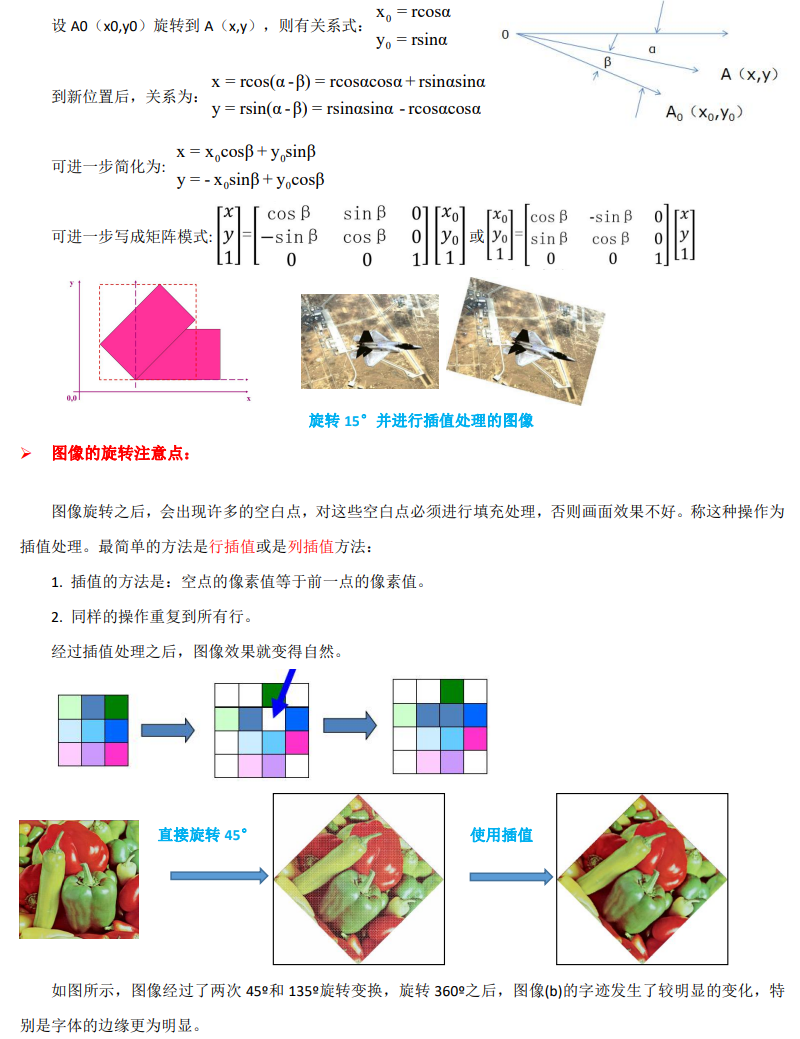
7. 灰度插值
图像的比例缩放、 旋转变换时等,变换过程需要两个独立的算法: 一个算法完成几何变换; 一个算法用于灰度级插值.
数字图像处理只能对坐标网格点(离散点)的值进行变换。而坐标变换后产生的新坐标值同网格点值往往不重合,因此需要通过内插的方法将非网格点的灰度值变换成网格点的灰度值,这种算法称为灰度内插。
最近邻插值法
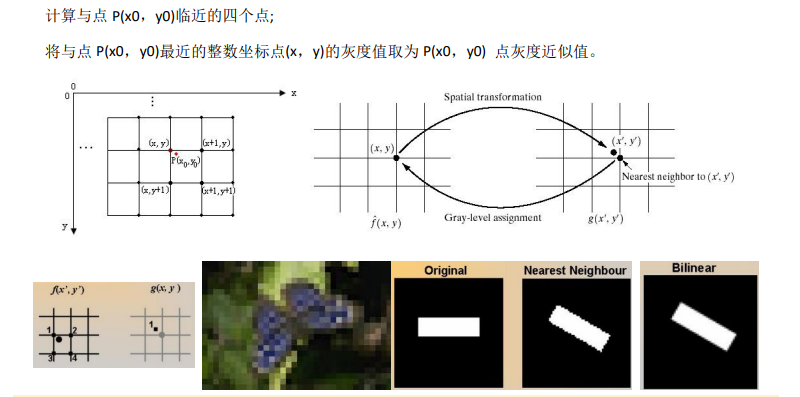
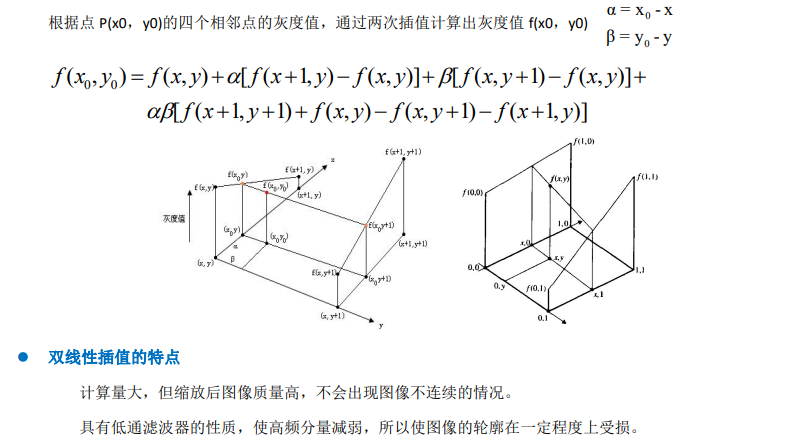
双线性插值法(一阶插值)
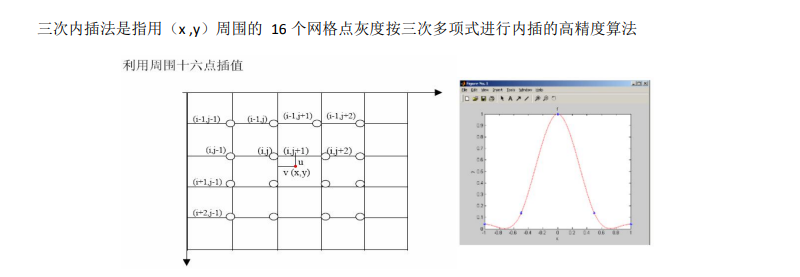
三阶插值
4 点运算


知识点:

5 代数运算
- 加运算:C(x,y) = A(x,y) + B(x,y),其中 C(x,y)为输出图像,A(x,y)、B(x,y)为输入图像。重要应用是对所获取的同一场景的多幅图像求平均,常常用来有效的削弱图像的加性随机噪声。
去除“叠加性”随机噪声,可以得到各种图像合成的效果,也可以用于两张图片的衔接
- 减运算:C(x,y) = A(x,y) - B(x,y),其中 C(x,y)为输出图像,A(x,y)、B(x,y)为输入图像。又称为减影技术,指对同一景物在不同时间拍摄的图像或同一景物在不同波段的图像进行相减。差值图像提供了图像间的差异信息,能用以指导动态监测,运动目标性检测和跟踪,图像背景消除及目标识别等工作。
消除背景影响(去除不需要的叠加性图案)
- 乘运算:C(x,y) = A(x,y) * B(x,y),其中 C(x,y)为输出图像,A(x,y)、B(x,y)为输入图像。可用来遮掉图像的某些部分。使用掩模图像(对需要被完整保留下来的区域,掩模图像上的值为 1,而对被抑制掉的区域则值为 0),去乘图像,可抹去图像的某些部分,即该部分值为 0。
图像的局部显示
- 除运算:C(x,y) = A(x,y) / B(x,y),其中 C(x,y)为输出图像,A(x,y)、B(x,y)为输入图像。图像相除又称比值处理,是遥感图像处理中常用的方法。可以利用比值图像使图像中各类地物均值拉开,方差缩小,从而易于区别各类,还能用于消除山影,云影及显示隐伏构造。
常用于遥感图像处理中
6 代数运算
- 非运算:g(x, y) = 255 - f(x, y)
应用:获得一个阴图像,获得一个子图像的补图像 - 与运算:g(x, y) = f(x, y)^ h(x, y)
应用:模板运算:提取感兴趣的子图像 - 或运算:g(x, y) = f(x, y)V h(x, y)
应用:合并子图像,模板运算:提取感兴趣的子图像 - 异或运算 g(x, y) = f(x, y) h(x, y)
应用:获得相交子图像
二、傅里叶变换、小波变换
1 傅里叶变换
(傅里叶变换的目的、作用、特点等,以及傅里叶变换后去掉频谱图中的高频、低频后的变化)


1.1 目的
- 简化计算,也即傅里叶变换可将空间域中复杂的卷积运算转化为频率域中简单的乘积运算;
- 对于某些在空间域中难以处理或处理起来比较复杂的问题,利用傅里叶变换把用空间域表示的图像映射到频率域,在利用频率域滤波或频域分析方法对其进行处理和分析,然后再把频域中处理和分析的结果变换回空间域,从而可达到简化处理和简化的目的
- 特殊目的的应用需求,比如通过某些频率域的处理方法,实现对图像的增强,特征提取,数据压缩,纹理分析,水印嵌入等,从而实现在空间域难以达到的效果。
1.2 作用
(1)可以得出信号在各个频率点上的强度。
(2)可以将卷积运算化为乘积运算。
(3)傅氏变换和线性系统理论是进行图像恢复和重构的重要手段。
(4)傅立叶变换能使我们从空间域与频率域两个不同的角度来看待图像的问题,有时在空间域无法解决的问题在频域却是显而易见的。
1.3 特点
概念:
也称作傅立叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。傅里叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅里叶变换用正弦波作为信号的成分。
优点:
傅立叶变换是将信号完全的放在频率域中分析,可以将一个时域信号转换成在不同频率下对应的振幅及相位,是连接时域与频域的桥梁。
缺点:
- 由于正弦波是无限宽度的,这使得被分析的信号也需要具有从负无穷大到正无穷大都有意义的特性,所以傅立叶变换不能很好的处理一些局部信号。比如,一个在局部范围内有非 0 值而其余所有地方都等于 0 的函数,它的频谱会呈现出一幅相当混乱的状况。这时,频域的信号反而不如时域的直观,频谱分析变得很艰难。
- 无法给出信号在每一个时间点的变化情况,并且对时间轴上任何点的突变都会影响整个频率的信号
1.4 频谱图


2 小波变换
(小波变换的应用)
概念:使用有限宽度基函数进行变换的方法。这些基函数不仅在频率上而且在位置上是变化的,这些有限宽度的波被称为 “小波”。基于它们的变换被称为 “小波变换” 。
特点:小波变换是以某些特定的函数为基(不止是一个),将数据信号展开成级数系列,它是时间和频率的局部变换,可同时在时域和频率中对数据进行多尺度联合分析,具有多尺度细化分析的功能。因此,我们可以在不同的分解层上和不同的小波基函数对信号进行有效的分析

3 联系与区别
联系:无论是傅立叶变换还是小波变换,其实质都是一样的,既:将信号在时间域和频率域之间相互转换,从看似复杂的数据中找出一些直观的信息,再对它进行分析。由于信号往往在频域有比在时域更加简单和直观的特性,所以,大部分信号分析的工作是在频域中进行的。
区别:
- 傅立叶变换作用在稳定信号上,小波变换对非稳定信号有很好的效果,这是 2 个变换的最根本的区别。
- 小波变换可以在频率上可以利用分解级数更细致的分辨率分析,傅立叶变换在固定的分辨率上进行分析的。
- 傅立叶变换提供了有关频率域的信息,但有关时间的局部化信息却基本丢失。与傅立叶变换不同,小波变换是通过缩放母小波的宽度来获得信号的频率特征, 通过平移母小波来获得信号的时间信息。对母小波的缩放和平移操作是为了计算小波系数,这些小波系数反映了小波和局部信号之间的相关程度。
三、图像增强、图像复原、图像退化
1 图像增强
1.1 概念
图像增强是数字图像处理的基本内容之一,其目的是根据应用需要突出图像中的某些“有用”信息,削弱或去除不需要的信息,以达到扩大图像中不同物体特征之间的差别。
图像增强算法并不能增加原始图像的信息,而是通过某种技术手段有选择地突出对某一具体应用有价值的信息。对于数字图像处理而言,噪声是指图像中的非本源信息。
因此,噪声会影响人的感官对所接收的信源信息的准确理解。
1.2 目的
- 改善图像的视觉效果。
- 突出图像的特征,便于计算机处理。
1.3 方法
法一:灰度变换
主要有空域处理法和频域处理法
(1)空域处理法:直接在图像所在的二维空间进行处理,即直接对每一像元的灰度值进行处理。
(2)频域处理法:将图像从空间域变换到频率域对图像进行处理。
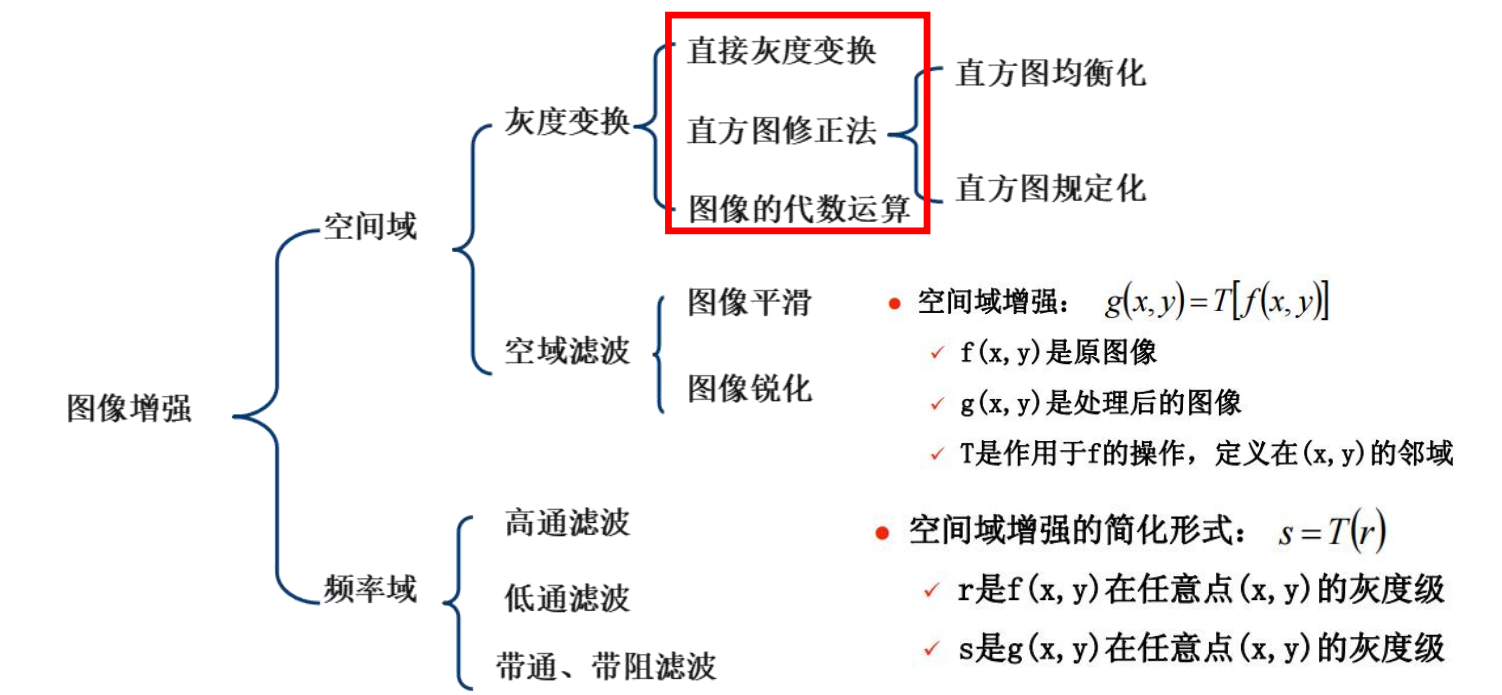
法二:空间域滤波增强
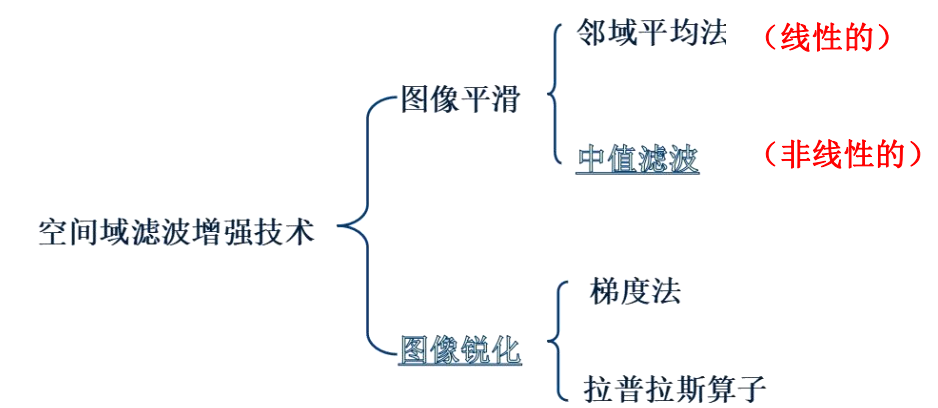
图像平滑:
均值滤波
中值滤波
图像锐化
一阶微分滤波器:梯度算子
二阶微分滤波器:拉普拉斯算子
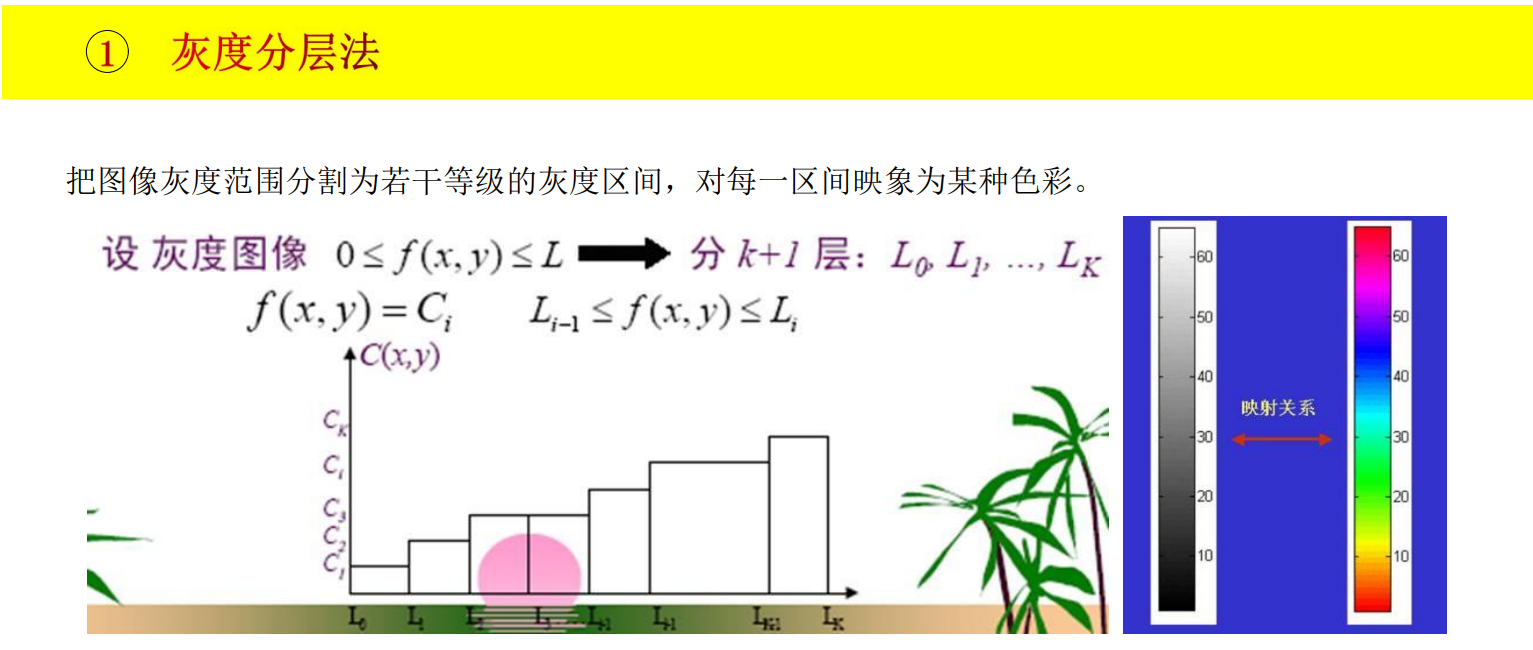
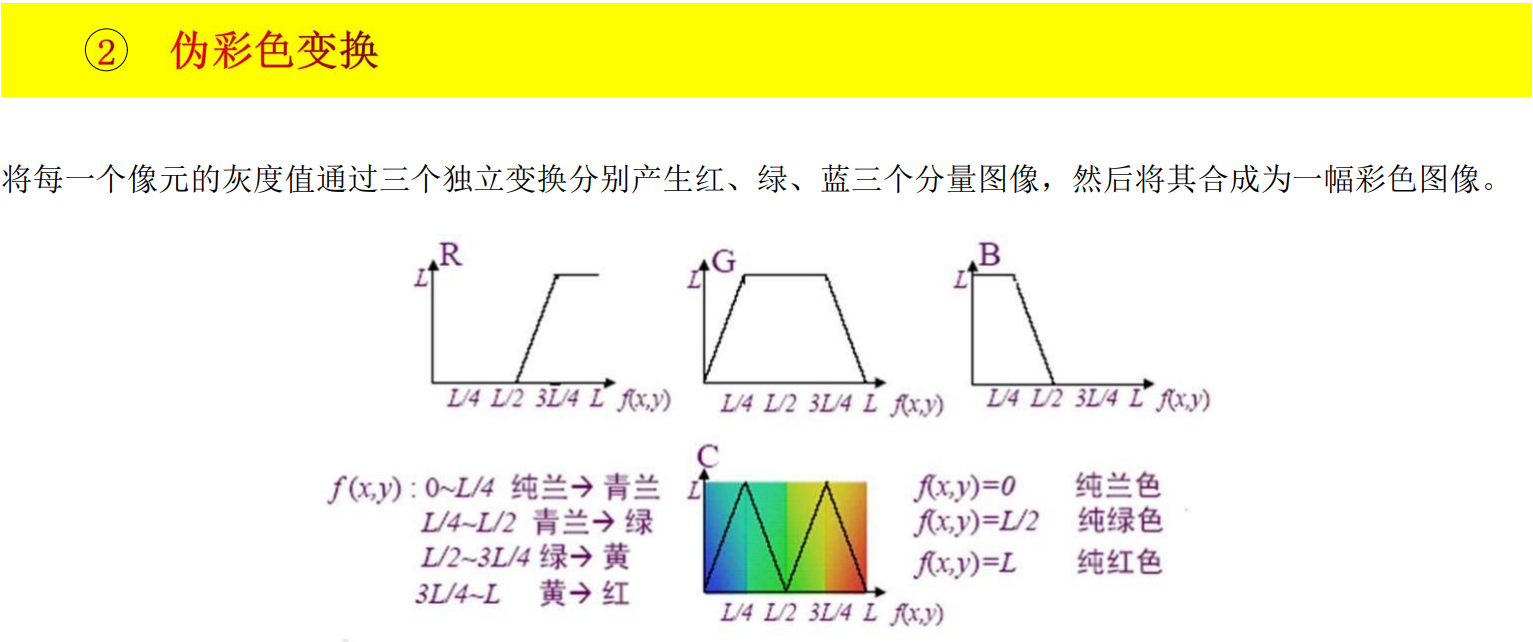
彩色增强

伪彩色增强法
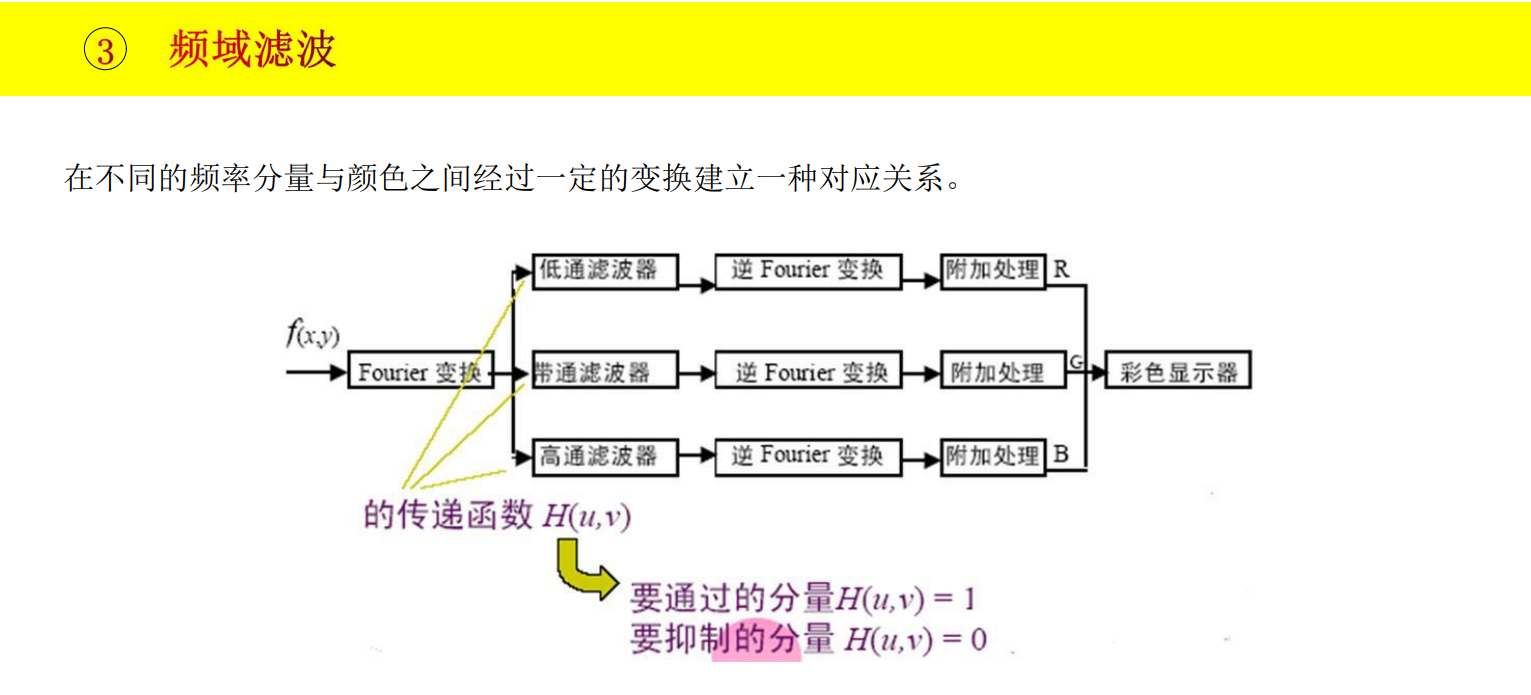

四、边缘检测算子
Roberts算子

Roberts 算子:边缘定位准,但是对噪声敏感。适用于边缘明显且噪声较少的图像分割。
Prewitt算子

Prewitt 算子:对噪声有抑制作用,抑制噪声的原理是通过像素平均,但是像素平均相当于对图像的低通滤波,所以 Prewitt 算子对边缘的定位不如 Roberts 算子。
Sobel算子
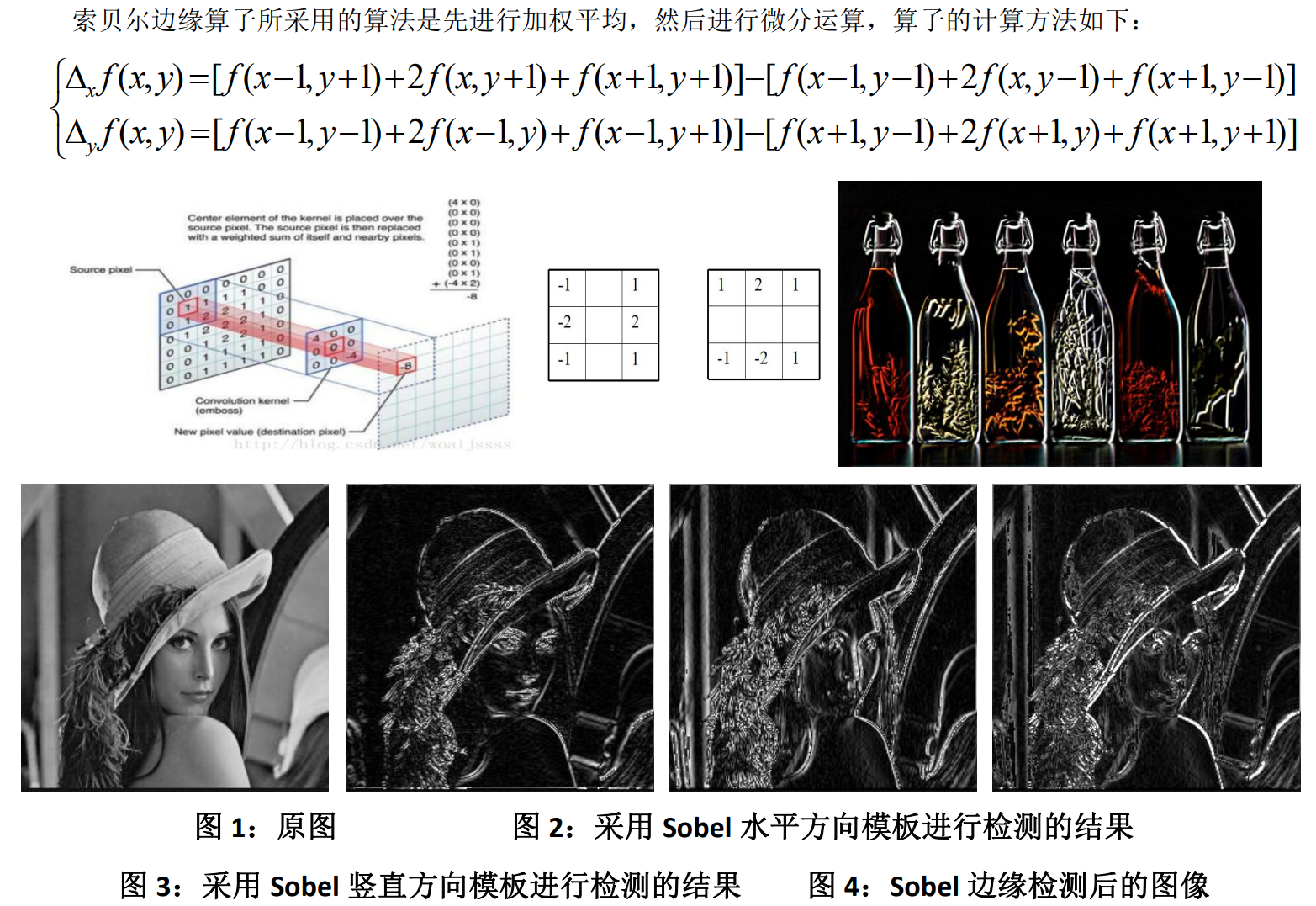
Sobel 算子:Sobel 算子和 Prewitt 算子都是加权平均,但是 Sobel 算子认为,邻域的像素对当前像素产生的影响不是等价的,所以距离不同的像素具有不同的权值,对算子结果产生的影响也不同。一般来说,距离越远,产生的影响越小
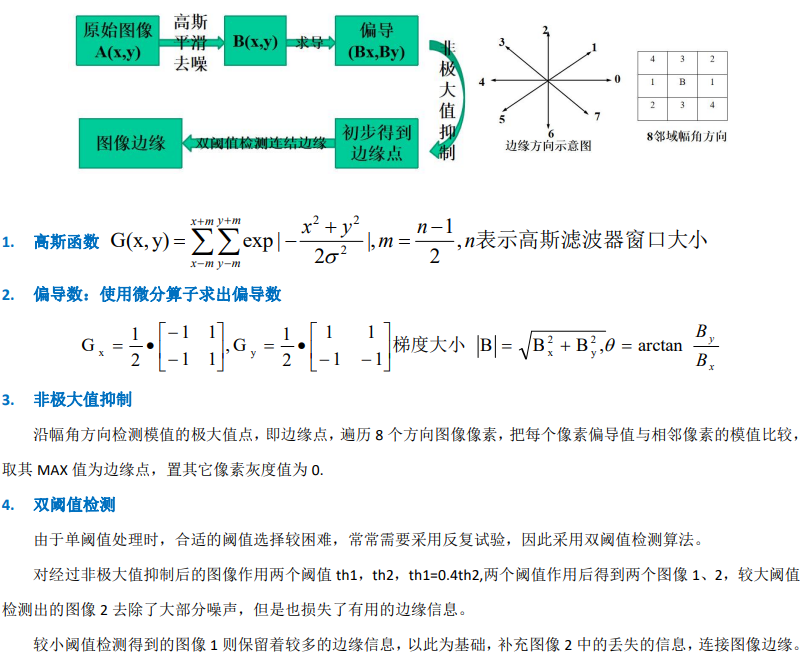
Canny算子
检测过程
Canny 边缘检测算子是 John F. Canny 于 1986 年开发出来的一个多级边缘检测算法。更为重要的是 Canny 创立了边缘检测计算理论(Computational theory of edge detection)解释这项技术如何工作,对边缘检测质量进行分析,提出三准则:低误判率、高定位精度、抑制虚假边缘
Canny 算子检测边缘的实质是求信号函数的极大值问题来判定图像边缘像素点。


五、计算题
灰度插值
直方图均衡化、直方图规定化
中值滤波、均值滤波
六、综合
1 什么是线性系统?线性系统具有哪些特征?

2 什么是线性移不变系统?它有哪些性质?移不变系统的物理意义是什么?

3 试写出调谐信号的函数形式?试写出传递函数的数学表达式?传递函数具有哪些重要性质?

4 什么是梯度?试写出二维连续系统与二维离散系统的梯度运算形式。

5 数字图像处理技术中,常见的梯度算子有哪些?

6 灰度变换主要分为哪几类?分别有什么作用?

7 代数运算可以分为哪几类?分别有什么特点?

8 简述如何将一幅 3×3 的图片放大 7/3 倍?如何将一幅 5×5 的图片缩小 3/5 倍?
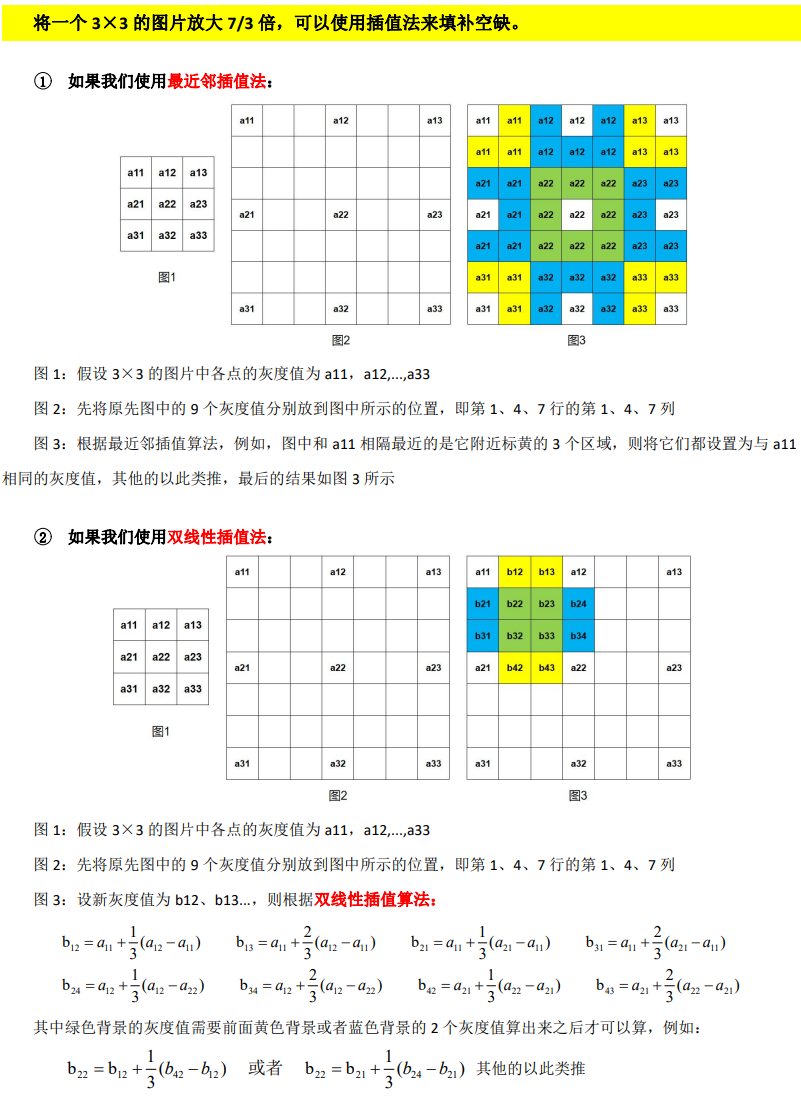
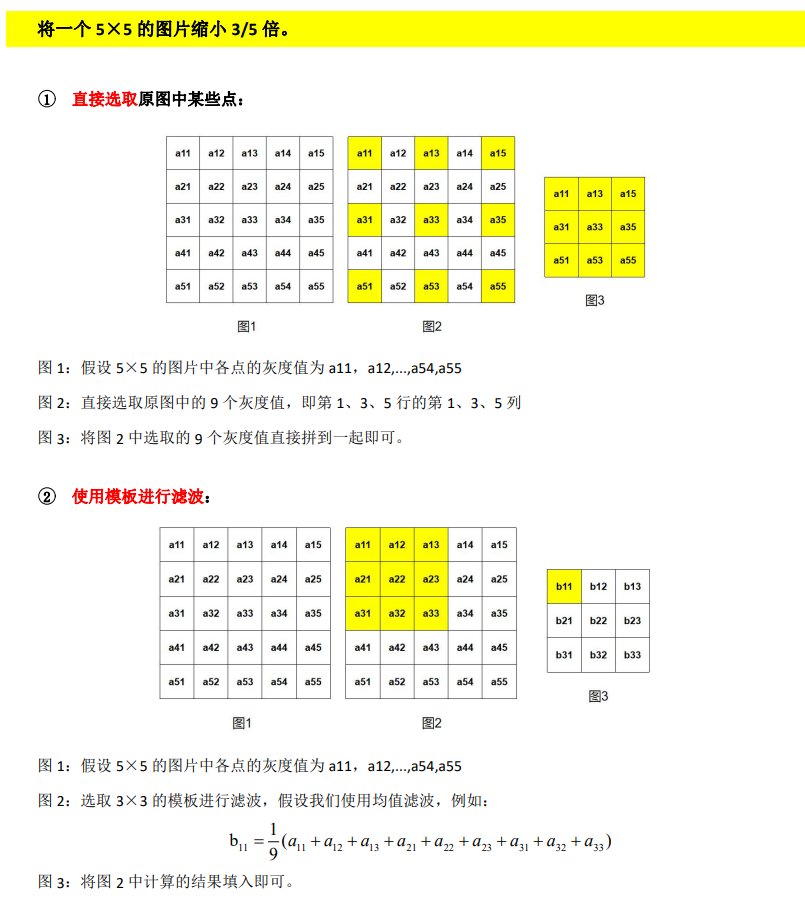
9 什么是傅里叶变换?傅立叶变换的作用有哪些?

10 傅里叶变换有哪些优缺点?有哪些应用?

11 什么是小波变换?它有什么特点?与傅里叶变换有什么区别?

12 傅里叶变换与小波变换有什么联系和区别?

13 一幅图像,经过傅里叶变换后,将高频/低频部分删除,再进行反变换,将会得到什么结果?为什么?
1)高频

2)低频

14 什么是图像增强?什么是图像退化?什么是图像复原?

15 图像增强的目的是什么?与图像复原有什么区别和联系?


16 图像复原的一般过程是什么?

17 比较 Laplacian 、Kirsch、Sobel 算子的不同?

18 比较 Roberts、Prewitt、Sobel 算子的不同?

19 简述 Canny 算子的检测过程?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号