【HNOI2016】树

题面

题解

这棵大树有\(10^{10}\)个点，光建出来就TLE + MLE，所以要谨慎打题。

发现每一次都是复制模板树的子树，所以这是一个真\(\cdot\)树套树。

构造大树的时候，令每一个大节点对应模板树的一整棵子树，然后对新树重新编号，就像这样：

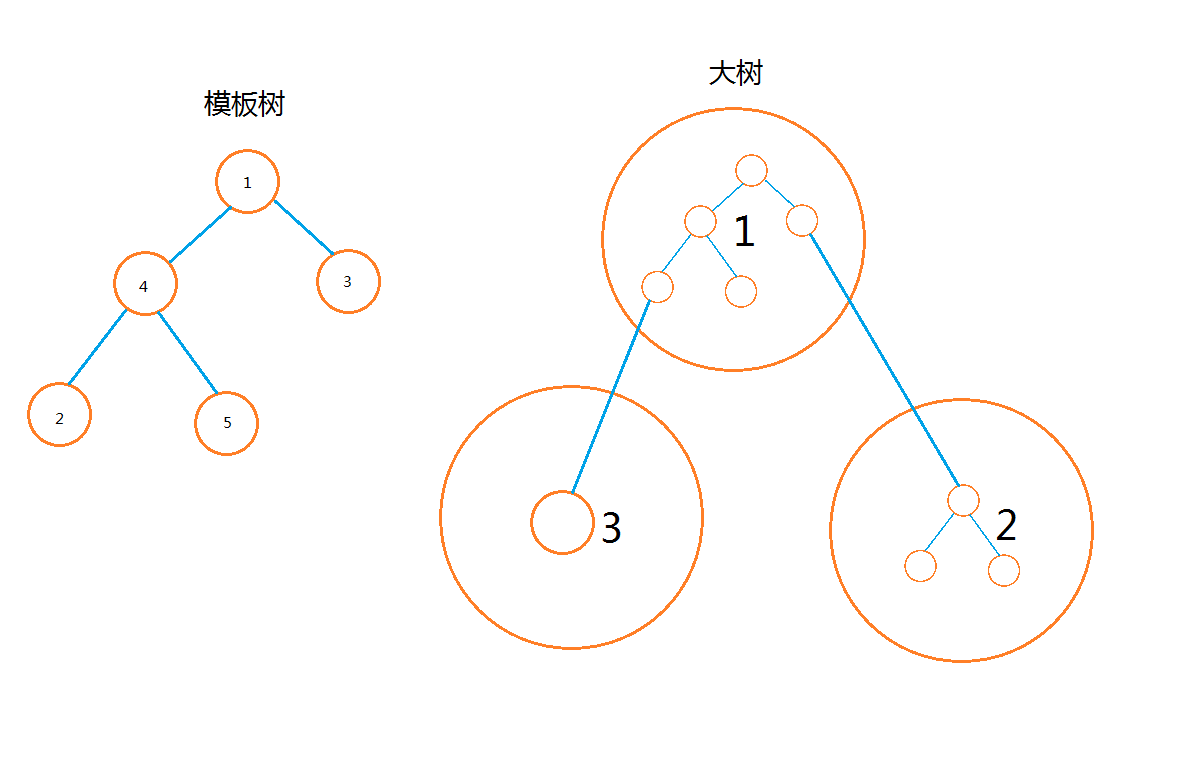
然后我们定义两个大节点之间的边的边权为两个大节点所包含的树的树根之间的距离。如上图中大节点\(1\)和\(2\)之间的边权为\(2,1\)与\(3\)之间的边权为\(3\)。

考虑如何计算答案。

我们可以在大树上用倍增求LCA，但是不能纯粹在大树上求LCA，需要注意很多的细节问题。

比如说再跳一步就重合时，要跳到上面那个节点的小模板树上面求LCA。

这道题目说起来挺简单，但是写起来就不一样了。

代码

不要在意x$这种变量名

#include<cstdio>
#include<cstring>
#include<cctype>
#include<algorithm>
#define RG register
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define clear(x, y) memset(x, y, sizeof(x))

inline int read()
{
	int data = 0, w = 1; char ch = getchar();
	while(ch != '-' && (!isdigit(ch))) ch = getchar();
	if(ch == '-') w = -1, ch = getchar();
	while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar();
	return data * w;
}

inline long long readl()
{
	long long data = 0, w = 1; char ch = getchar();
	while(ch != '-' && (!isdigit(ch))) ch = getchar();
	if(ch == '-') w = -1, ch = getchar();
	while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar();
	return data * w;
}

const int maxn(1e5 + 10), LogN(20);
int n, m, Q, Log[maxn];
namespace Ptree
{
	int root[maxn], lson[maxn * LogN], cur;
	int rson[maxn * LogN], size[maxn * LogN];
	void build(int &x, int l = 1, int r = ::n)
	{
		x = ++cur; if(l == r) return;
		int mid = (l + r) >> 1;
		build(lson[x], l, mid);
		build(rson[x], mid + 1, r);
	}

	void insert(int &x, int v, int l = 1, int r = ::n)
	{
		int x$ = ++cur; lson[x$] = lson[x], rson[x$] = rson[x];
		size[x$] = size[x] + 1; x = x$; if(l == r) return;
		int mid = (l + r) >> 1;
		if(v <= mid) insert(lson[x], v, l, mid);
		else insert(rson[x], v, mid + 1, r);
	}

	int query(int x, int y, int k, int l = 1, int r = ::n)
	{
		if(l == r) return l;
		int mid = (l + r) >> 1, s = size[lson[y]] - size[lson[x]];
		if(k <= s) return query(lson[x], lson[y], k, l, mid);
		else return query(rson[x], rson[y], k - s, mid + 1, r);
	}
}

namespace Template
{
	int fa[LogN][maxn], dep[maxn], pos[maxn], end_pos[maxn], cnt, cnt_pos[maxn];
	struct edge { int next, to; } e[maxn << 1];
	int head[maxn], e_num;
	inline void add_edge(int from, int to)
	{
		e[++e_num] = (edge) {head[from], to};
		head[from] = e_num;
	}

	void dfs(int x, int f)
	{
		cnt_pos[pos[x] = ++cnt] = x; fa[0][x] = f; dep[x] = dep[f] + 1;
		for(RG int i = 1; i < LogN; i++) fa[i][x] = fa[i - 1][fa[i - 1][x]];
		for(RG int i = head[x]; i; i = e[i].next)
			if(e[i].to != f) dfs(e[i].to, x);
		end_pos[x] = cnt;
	}

	int Dis(int x, int y)
	{
		if(dep[x] < dep[y]) std::swap(x, y);
		int ret = dep[x] - dep[y];
		for(RG int i = LogN - 1; ~i; i--)
			if(dep[fa[i][x]] >= dep[y]) x = fa[i][x];
		if(x == y) return ret;
		for(RG int i = LogN - 1; ~i; i--) if(fa[i][x] != fa[i][y])
			ret += 1 << (i + 1), x = fa[i][x], y = fa[i][y];
		return ret + 2;
	}
}

namespace BigTree
{
	int n, fa[LogN][maxn], dep[maxn], pre[maxn];
	long long dis[LogN][maxn], pos[maxn], end_pos[maxn], cur, link[maxn];
	int getRoot(long long x)
	{
		int l = 1, r = n;
		while(l <= r)
		{
			int mid = (l + r) >> 1;
			if(pos[mid] <= x) l = mid + 1;
			else r = mid - 1;
		}
		return r;
	}

	int getPre(long long x)
	{
		int rt = getRoot(x);
		return Ptree::query(Ptree::root[Template::pos[pre[rt]] - 1],
				Ptree::root[Template::end_pos[pre[rt]]], x - pos[rt] + 1);
	}

	void Init()
	{
		pos[1] = n = dep[1] = pre[1] = 1; cur = end_pos[1] = ::n;
		int x; long long to;
		for(RG int i = 1; i <= m; i++)
		{
			x = read(), to = readl(); int rt = getRoot(to);
			++n, dep[n] = dep[rt] + 1, link[n] = to, pre[n] = x;
			pos[n] = cur + 1, end_pos[n] = cur + Template::end_pos[x]
				- Template::pos[x] + 1; cur = end_pos[n];
			fa[0][n] = rt; dis[0][n] = Template::dep[getPre(to)] -
				Template::dep[pre[rt]] + 1;
			for(RG int j = 1; j < LogN; j++)
				fa[j][n] = fa[j - 1][fa[j - 1][n]],
				dis[j][n] = dis[j - 1][n] + dis[j - 1][fa[j - 1][n]];
		}
	}

	long long Dis(long long x, long long y)
	{
		long long ans = 0; int fx = getRoot(x), fy = getRoot(y);
		if(fx == fy) return Template::Dis(getPre(x), getPre(y));
		if(dep[fx] < dep[fy]) std::swap(x, y), std::swap(fx, fy);
		ans += Template::dep[getPre(x)] - Template::dep[pre[fx]], x = fx;
		for(RG int i = LogN - 1; ~i; i--) if(dep[fa[i][x]] > dep[fy])
			ans += dis[i][x], x = fa[i][x];
		if(getRoot(link[x]) == fy)
			return ans + 1 + Template::Dis(getPre(link[x]), getPre(y));
		ans += Template::dep[getPre(y)] - Template::dep[pre[fy]], y = fy;
		if(dep[x] > dep[y]) ans += dis[0][x], x = fa[0][x];
		for(RG int i = LogN - 1; ~i; i--) if(fa[i][x] != fa[i][y])
			ans += dis[i][x] + dis[i][y], x = fa[i][x], y = fa[i][y];
		x = link[x], y = link[y]; ans += 2;
		return ans + Template::Dis(getPre(x), getPre(y));
	}
}

int main()
{
	n = read(), m = read(), Q = read(); Log[0] = -1;
	for(RG int i = 1; i <= n; i++) Log[i] = Log[i >> 1] + 1;
	for(RG int i = 1, a, b; i < n; i++)
		a = read(), b = read(),
		Template::add_edge(a, b),
		Template::add_edge(b, a);
	Template::dfs(1, 0); Ptree::build(Ptree::root[0]);
	for(RG int i = 1; i <= n; i++)
		Ptree::root[i] = Ptree::root[i - 1],
		Ptree::insert(Ptree::root[i],
			Template::cnt_pos[i]);
	BigTree::Init(); long long x, y;
	while(Q--) x = readl(), y = readl(), printf("%lld\n", BigTree::Dis(x, y));
	return 0;
}