【HNOI2014】米特运输
题面
题解
首先我们需要看懂题目
然后我们需要发现一个结论
只要有一个节点的权值确定,那么整棵树的权值就确定了
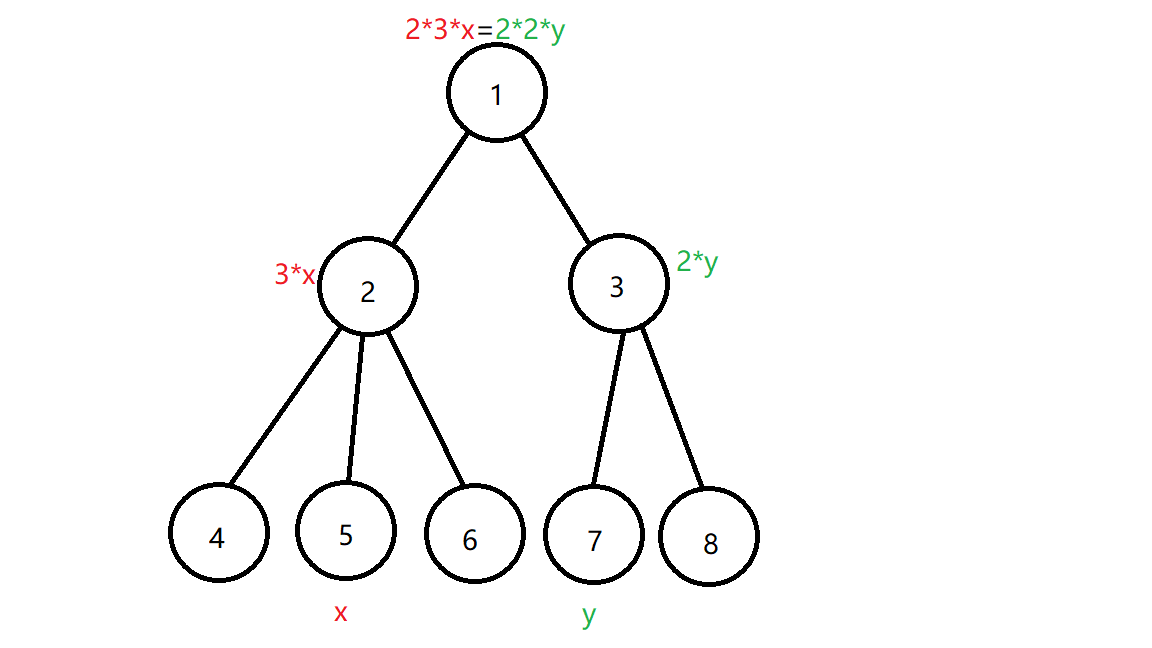
就像这样:(图片来源于网络,侵删)
然后我们根据这张图片,可以设\(f[i] = a[i] \cdot \prod_f \mathrm{son}[f]\)
其中\(f\)是\(i\)的祖先,\(\mathrm{son}[f]\)表示\(f\)的子节点的个数,\(a[i]\)表示\(i\)的权值
于是我们可以用显然法证明当\(f[i] = f[j]\)时,\(i\)和\(j\)的权值肯定在一种方案中都不用修改
于是算出最多有多少点的\(f\)值相等
然后你愉快地打了上去,oho了
\(f[]\)会爆long long,于是考虑取对数就可以了
普及公式:\(\log_c a + \log_c b = \log_c (ab)\)
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cctype>
#include<algorithm>
#define RG register
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define clear(x, y) memset(x, y, sizeof(x))
inline int read()
{
int data = 0, w = 1; char ch = getchar();
while(ch != '-' && (!isdigit(ch))) ch = getchar();
if(ch == '-') w = -1, ch = getchar();
while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar();
return data * w;
}
const double eps(1e-8);
const int maxn(500010);
struct edge { int next, to; } e[maxn];
int head[maxn], e_num, n, a[maxn], deg[maxn];
double f[maxn];
inline void add_edge(int from, int to)
{
e[++e_num] = (edge) {head[from], to};
head[from] = e_num;
}
void dfs(int x, double s)
{
f[x] = s + log(a[x]);
for(RG int i = head[x]; i; i = e[i].next)
dfs(e[i].to, s + log(deg[x]));
}
int main()
{
n = read();
for(RG int i = 1; i <= n; i++) a[i] = read();
for(RG int i = 1, a, b; i < n; i++)
a = read(), b = read(), ++deg[a], add_edge(a, b);
dfs(1, 0); std::sort(f + 1, f + n + 1); int ans = 1;
for(RG int i = 2, cnt = 1; i <= n; i++)
{
if(f[i] - f[i - 1] <= eps) ans = std::max(ans, ++cnt);
else cnt = 1;
}
printf("%d\n", n - ans);
return 0;
}