15C++循环结构-while循环(2)
一、while语句的应用
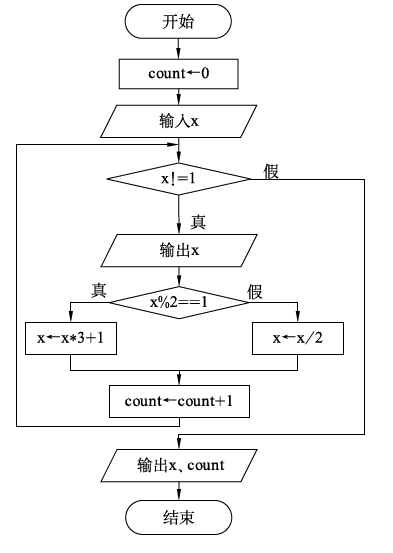
问题:对于每一个正整数,如果它是奇数,则对它乘3再加1,如果它是偶数,则对它除以2,如此循环,最终都能够得到1,这就是由日本数学家角谷静夫发现的角谷猜想,又称为3n+1猜想。如取一个数字6,根据上述公式,得出6→3→10→5→16→8→4→2→1。试编一程序,验证角谷猜想。
流程图:
#include <iostream>
using namespace std;
int main()
{
long long x,count=0;
cout<<"x=";
cin>>x;
while(x!=1)
{
cout<<x<<"---->";
if(x%2==1) x=x*3+1;
else x/=2;
count++;
}
cout<<x<<endl;
cout<<"步数:"<<count<<endl;
return 0;
}
练习:
(1)格莱尔在参加信息学社团的学习过程中,想在因特网上与他人行即时讨论、交流,则下列工具中最适合的是()。
A.E-mail(电子邮件) B.BBS(电子公告栏) C.QQ D.博客
(2)阅读程序写结果。
#include <iostream>
using namespace std;
int main()
{
int n, x, s=0;
cin>>n;
x=n;
while(x>=1)
{
if(n%x==0)++s;
--x;
cout <<s<< endl;
return 0;
}
输入:8
n,x,s输出:_____________
3.完善程序。
计算2020-1+2-3+4-5+··±n的值(n为奇数时减,偶数时加)。
#include <iostream>
using namespace std;
int main()
{
int i, sum, n;
_______________;
cout <<"n=";
cin>>n;
i=l;
while(i<=n)
{
if(_____)
sum-=i;
else
sum+=i;
i++;
}
cout << sum << endl;
return 0;
}
二、双精度实数double及科学计数法
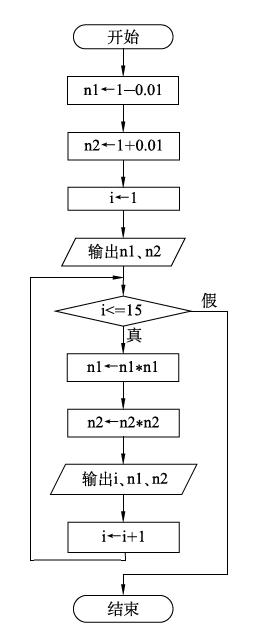
一只蝴蝶在巴西轻拍翅膀,可以导致一个月后美国得克萨斯州的一场龙卷风,一只海鸥扇动翅膀足以改变天气,这是美国气象学家爱德华·诺顿·罗伦兹在1963年提出的蝴蝶效应,表明初始条件的极小偏差,将会引起结果的极大差异。n的初始值设为1,让它产生极小偏差。减0.01后得到的值是0.99,加0.01后得到的值是1.01,以后每次得到的值都是自己乘自己。试编一程序算一算,第15次后分别是多少?
流程图如图:
#include <iostream>
using namespace std;
int main()
{
int n,i;
double n1,n2;
n=1;
n1=n-0.01;
n2=n+0.01;
cout<<" "<<n1;
cout<<" "<<n2<<endl;
i=1;
while(i<=15)
{
n1*=n1;
n2*=n2;
cout<<i<<" "<<n1<<" "<<n2<<endl;
i++;
}
return 0;
}
运行结果:
1 0.9801 1.0201
2 0.960596 1.0406
........
14 3.06922e-072 6.32977e+070
15 9.42012e-144 4.0066e+141
其中1.15048e-009、7.08229e+008等数字是什么意思啊?
实数又称为浮点数,类型包括正实数、负实数、实数零,如12.8、-6.3、0.0都是实数。其中0.0是实数零,而0是整数零。实数有两种表示方法,一种是日常表示法,如3.14159、-0.6等;另一种是科学计数法,如7.9e+2、6.18e-1等。
科学计数法是采用指数形式表示实数,每个数由只含一位整数的数和指数两部分组成。如:
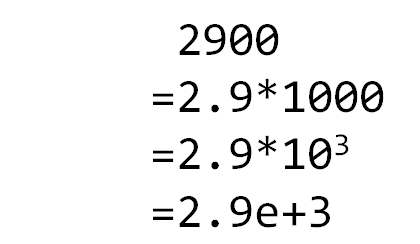
1.15048e-009=0.00000000115048(小数点向左移动9位)
7.08229e+008=708229000(小数点向右移动8位)
double为双精度实数(双精度浮点数),可表示的范围为-1.79e308~1.79e308。
练习:
(1)用科学计数法表示2600,以下( )是正确的。
A.2.6e+2 B.2.6e+3 C.2.6e-2 D.2.6e-3
(2)阅读程序写结果。
#include <iostream>
using namespace std;
int main()
{
int n, x, s=0;
cin>>n;
x=1;
while(x<=n)
{
if(x%3==1)s+=x;
++x;
}
cout <<s<< endl;
return 0;
}
输入:20
n,x,s输出:_____________
(3)完善程序。
韩信带1500名士兵打仗,战死四五百人,幸存的士兵站3人一排,多出2人;站5人一排,多出4人;站7人一排,多出6人,算一算幸存的兵至少有多少人?
#include <iostream>
using namespace std;
int main()
{
int i;
i=1000;
while(true)
{
if(i%3==2&&i%5==4&&i%7==6) _____________;
i++;
}
cout <<___________<<endl;
return 0;
}
三、分数化为小数
问题:在科学研究的领域,对数据的精度求非高,有时需计算到小数点后10位,甚至小数点后100位,做到精益求精。
试编一程序,把分数1/7转化成小数的形式,要求计算结果精确到小数点100位。
先看下尼克初学时编写的程序:
#include<iostream>
using mamespace sid;
int main()
{
cout<<1/7<<endl;
cout<< 1.0/7<endl;
reurn 0;
}
其中(double)1/7。运用了强制类型转换运算符,将结果转换成双精度浮点数,但还不能输出小数点后100位,要解决此问题,我们先来研究一下1/7的运算过程。
1÷7=0·········1
1×10÷7=1······3(商1,小数点后第1位上的数字)
3×10÷7-4······2(商4,小数点后第2位上的数字)
2×10÷7=2······6(商2,小数点后第3位上的数字)
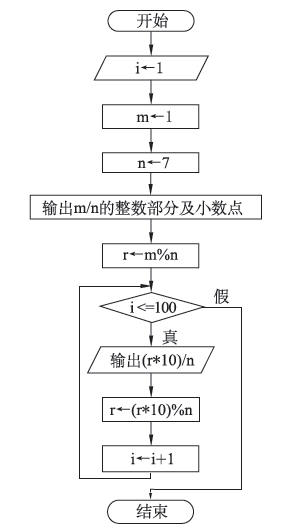
把上一次产生的余数扩大10倍,再除以7,得到的商就是当前数位上的数字。流程图如图:
#include <iostream>
using namespace std;
int main()
{
int m,n,r,i=1;
m=1;
n=7;
cout<<m/n<<'.';
r=m%n;
while(i<=100)
{
cout<<(r*10)/n;
r=(r*10)%n;
i++;
}
return 0;
}
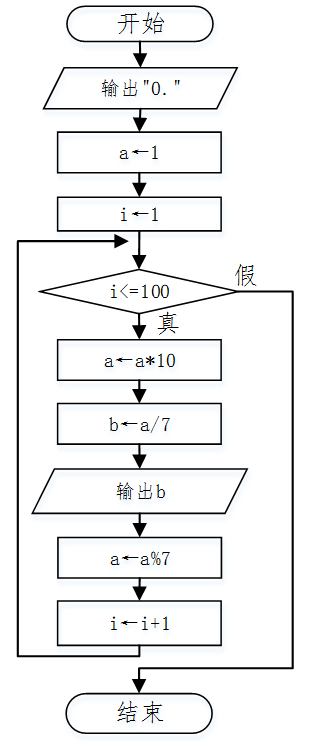
#include <iostream>
using namespace std;
int main()
{
int a,b,i;
cout<<"0.";
i=1;
a=1;
while(i<=100)
{
a*=10;
b=a/7;
cout<<b;
a%=7;
i++;
}
return 0;
}
练习:
(1)在计算机内部,一切信息存取、处理和传递的形式都是( )。
A.ASCII码 B.BCD码 C.二进制 D.十六进制
(2)阅读程序写结果:
#include<iostream>
using namespace std;
int main()
{
int a, b, n, num=0;
cin>>a>>b>>n;
while(a<=b)
{
if(a%n==0)num++;
a++;
b=-10;
}
cout << num <<endl;
return 0 ;
}
输入:1 100 5
a,b,n,num输出:_______________
(3)完善程序。
输入三个正数a、b、n,输出a÷b的值,要求计算结果精确到小数点后n(1≤n≤200)位。如输人1 3 4,出0.33;输入2017 27 10,输出74.7037037037。
#include<iostream>
using namespace std;
int main()
{
int a,b,n,ans,i;
cout<<"a b n=";
cin>>a>>b>>n;
____________;
cout<<ans;
cont<<'.';
a%=b;
for(i=1;i<=n;i++)
{
ans=(a*10)/b;
cout<<ans;
_________;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号