08-01集合运算
集合运算
交集运算
存在集合A和B, 对于集合C, 如果C的每个元素即是A的元素, 又是B的元素, 并且A和B所有相同的元素都在C找到, 那么C是A和B的交集。具体请参考如下实例。
交集运算方法:
- s1.intersection(s2)
- s1.intersection_update(s2):_update版本, 原地修改, 返回None
- &:s1 & s2,也叫交集运算符重载
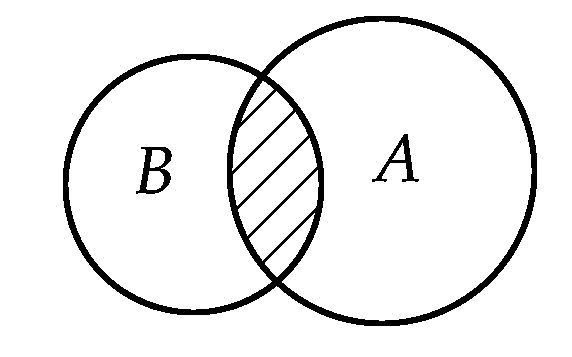
实例1:s1.intersection(s2)
In [82]: s1 = {1, 2, 3}
In [83]: s2 = {2, 3, 4}
In [84]: s1.intersection(s2) # 交集
Out[84]: {2, 3}
In [85]: s2.intersection(s1) # 不修改原来的两个集合, 返回新的集合
Out[85]: {2, 3}
In [86]: s1
Out[86]: {1, 2, 3}
In [87]: s2
Out[87]: {2, 3, 4}
实例2:s1.intersection_update(s2)
In [88]: s1.intersection_update(s2) # _update版本, 原地修改, 返回None, 等效于s1 = s1.intersection(s2)
实例3:s1 & s2
In [89]: s1
Out[89]: {2, 3}
In [90]: s2
Out[90]: {2, 3, 4}
In [91]: s1 = {1, 2, 3}
In [92]: s1 & s2 # set重载按位与运算符为求交集运算, 等效于s1.intersection(s2)
Out[92]: {2, 3}
In [93]: s2 & s1
Out[93]: {2, 3}
差集运算
结合A和B, 当集合C的元素仅存于A中, 但不存在B中, 并且A中存在B中不存在的元素全部存在C中, 那么C是A和B的差集。
差集运算方法:
- s1.difference(s2):求s1和s2的差集部分
- s1.difference_update(s2):_update版本原地修改, 返回None
- -:s1 - s2或者s2 - s1,也叫差集运算符重载
差集没有交换律
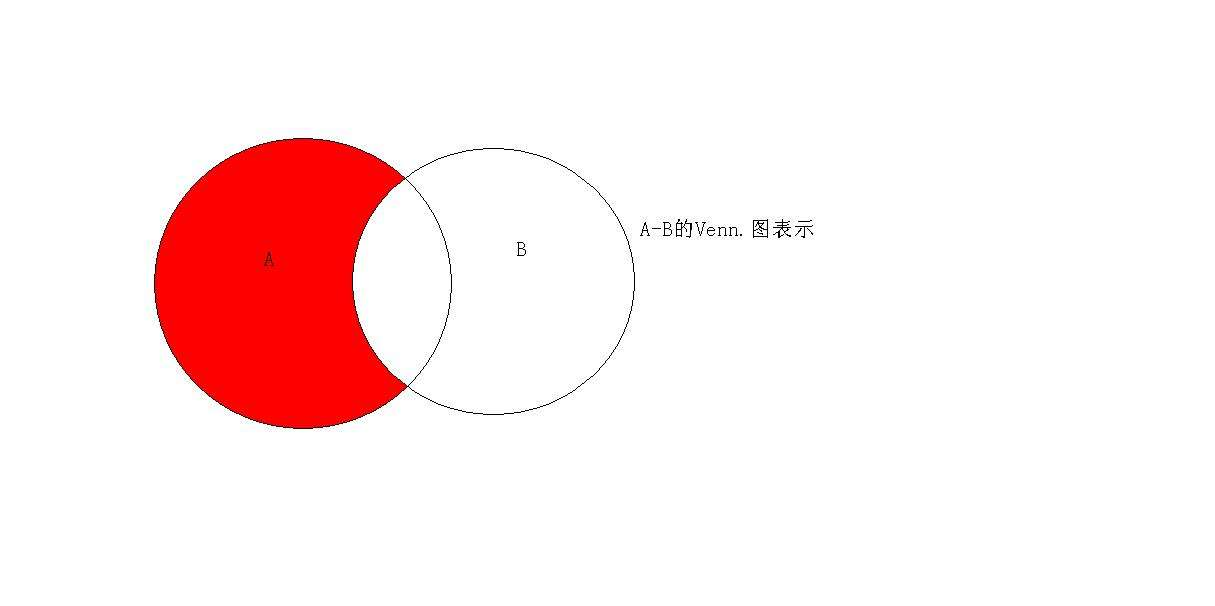
实例1:s1.difference(s2)
In [86]: s1
Out[86]: {1, 2, 3}
In [87]: s2
Out[87]: {2, 3, 4}
In [94]: s1.difference(s2) # 差集,求s1和s2的差集部分,意思是s1和s2对比,返回s1在s2没有的部分
Out[94]: {1}
结合A和B, 当集合C的元素仅存于A中, 但不存在B中, 并且A中存在B中不存在的元素全部存在C中, 那么C是A和B的差集。
实例2:s2.difference(s1)
In [95]: s2.difference(s1) # 差集没有交换律,求s2和s1的差集部分
Out[95]: {4}
实例3:s1.difference_update(s2)
In [96]: s1.difference_update(s2) # _update版本原地修改, 返回None, 相当于s1 = s1.difference(s2)
In [97]: s1
Out[97]: {1}
In [98]: s2
Out[98]: {2, 3, 4}
In [99]: s1 = {1, 2, 3}
实例4:s1 - s2
In [100]: s1 - s2 # set重载了运算符"-"执行差集计算, 相当于s1.difference(s2)
Out[100]: {1}
In [101]: s2 - s1
Out[101]: {4}
补集计算
如果把两个集合A和B看成是一个全集, 对称差集是交集的补集。
补集也叫对称差集。
补集运算方法:
- s1.symmetric_difference(s2)对称差集
- s1.symmetric_difference_update(s2),原地修改, 返回None
- ^:s1 ^ s2:补集的运算符重载
对称差集具有交换律
如下图:集合A和集合B不相交的部分

In [102]: s1.symmetric_difference(s2) # 对称差集
Out[102]: {1, 4}
In [103]: s2.symmetric_difference(s1) # 对称差集具有交换律
Out[103]: {1, 4}
In [104]: s1.symmetric_difference_update(s2) 原地修改, 返回None, 相当于None s1 = s1.symmetric_difference(s2)
In [105]: s1 = {1, 2, 3}
In [106]: s1 ^ s2 # set重载了异或运算符, 执行对称差集运算, 相当于s1.symmetric_difference(s2)
Out[106]: {1, 4}
并集计算
给定两个集合A,B,把他们所有的元素合并在一起组成的集合,叫做集合A与集合B的并集
并集运算方法:
- s1.union(s2)
- s1.update(s2)并集的update版本
- |:并集的运算符重载
In [107]: s1.union(s2) # 并集计算
Out[107]: {1, 2, 3, 4}
In [108]: s2.union(s1) # 有交换律
Out[108]: {1, 2, 3, 4}
In [109]: s1.update(s2) # 并集的update版本
In [110]: s1
Out[110]: {1, 2, 3, 4}
In [111]: s1 + s2 # 集合并没有重载加法运算符
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-111-1659087814e1> in <module>()
----> 1 s1 + s2
TypeError: unsupported operand type(s) for +: 'set' and 'set'
In [112]: s1 | s2 # set重载了按位或运算符, 用于并集计算
Out[112]: {1, 2, 3, 4}
集合的四种运算
补集的定义依赖于全集, python没有全集, 自然没有补集。
全集不是运算, 全集是定义出来的。

本图片来自于:https://blog.csdn.net/sxingming/article/details/51922776
集合相关的判断
- s2.issubset(s1):判断s2是否是s1的子集
- s1.issuperset(s2):判断s1是否是s2的超集
- 元素一样, 即是子集, 又是超集。比如这样s1.issuperset(s1)
- s1.isdisjoint(s2):判断两个集合是否有交集, 如果有交集返回False, 没有交集返回True
In [113]: s1 = {1, 2, 3, 4}
In [114]: s2 = {2, 3}
集合A里的所有元素都能在集合B里找到, 那么A是B的子集, B是A的超集
In [115]: s2.issubset(s1) # 判断s2是否是s1的子集
Out[115]: True
In [116]: s1.issubset(s2)
Out[116]: False
In [117]: s1.issuperset(s2) # 判断s1是否是s2的超集
Out[117]: True
In [118]: s1.issubset(s1) # 元素一样, 即是子集, 又是超集
Out[118]: True
In [119]: s1.issuperset(s1)
Out[119]: True
issubset的实现
In [120]: def issubset(s1, s2):
...: for x in s1:
...: if x not in s2:
...: return False
...: return True
...:
issuperset的实现
In [3]: def issuperset(s1, s2):
...: for x in s2:
...: if x not in s1:
...: return False
...: return True
...:
In [3]: s1.isdisjoint(s2) # 判断两个集合是否有交集, 如果有交集返回False, 没有交集返回True
Out[3]: False
In [4]: s3 = {1, 2}
In [5]: s4 = {3, 4}
In [6]: s3.isdisjoint(s4)
Out[6]: True
集合的应用
- 场景1:有一个api, 它需要认证, 并且有一定的权限才可以访问, 例如要求满足权限A, B, C中任意一项, 有一个用户具有权限B, C, D, 那么此用户是否有权限访问此API。
- 场景2:有一个任务列表, 存储全部的任务, 有一个列表, 存储已经完成的任务, 找出未完成的任务。
集合的限制
集合的特性, 元素不会重复
哪些数据结构对元素有限制?
- 集合能输入str、int、元组、bytes等
- 集合不能输入列表、bytearray、集合
In [7]: {'a', 'b', 'c'} # 集合能输入文本
Out[7]: {'a', 'b', 'c'}
In [8]: {1, 'b'} # 集合能输入数字及文本
Out[8]: {'b', 1}
In [9]: {1, 2, 3} # 集合能输入数字
Out[9]: {1, 2, 3}
In [10]: {[1, 2, 3], [2, 3, 4]} # 列表不能是集合的元素
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-10-7ca6f92cfb85> in <module>()
----> 1 {[1, 2, 3], [2, 3, 4]}
TypeError: unhashable type: 'list'
In [11]: {bytearray(b'abc')} # bytearray不能是集合的元素
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-11-62b530a8195b> in <module>()
----> 1 {bytearray(b'abc')}
TypeError: unhashable type: 'bytearray'
In [12]: {{3}} # 集合不能是集合的元素
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-12-dbb470487147> in <module>()
----> 1 {{3}}
TypeError: unhashable type: 'set'
In [13]: {(1, 2)} # 元组可以做为集合的元素
Out[13]: {(1, 2)}
In [14]: {b'abc'} # bytes可以做为集合的元素
Out[14]: {b'abc'}
In [16]: hash(b'abc') # bytes是可hash的
Out[16]: 7310675750012804621
In [17]: hash(1) # 数字是可hash
Out[17]: 1
In [18]: hash([1, 2, 3]) # 列表是不可hash的
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-18-0b995650570c> in <module>()
----> 1 hash([1, 2, 3])
TypeError: unhashable type: 'list'
目前我们所知道的所有的可变类型都是不可hash的, 所有的不可变类型都是可hash
hash是调用了元素的方法:
In [20]: 1.__hash__()
集合和集合操作总结
增加:
add
update
删除:
remove
discard
pop
clear
集合判断:
超集:
issuperset
子集:
isubset
交集:
isdisjoint
集合运算
交:
intersection
intersection_update
&
并:
union
update
|
差:
difference
difference_update
-
对称差集
symmetric_difference
symmetric_difference_update


