散列表解决冲突的方式

1. 开放定址法

开放定址法就是一旦发生冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

H_i = (H(key) + d_i) MOD m, i=1,2,…, k(k<=m-1)，其中H(key)为散列函数，m为散列表长，d_i为增量序列。d_i可有下列三种取法：

（1）d_i=1,2,3,…, m-1，称为线性探测再散列；

　　缺点：造成大量元素在相邻的散列地址上“聚集”，大大降低查找效率。

（2）d_i=1^2, -(1^2), 2^2, -(2^2), 3^2, …, ±(k^2),(k<=m/2)，称为二次探测再散列；

　　优点：避免出现“堆积”问题。

　　缺点：不能探测到散列表上的所有单元，但至少能探测到一半单元。

（3）d_i=伪随机数序列，称为伪随机探测再散列。

　　缺点：用同样的随机种子，将得到相同的数列。

 

缺点：

①存储记录的数目不能超过桶数组的长度，如果超过就需要扩容，而扩容会导致某次操作的时间成本飙升，这在实时或者交互式应用中可能会是一个严重的缺陷

②使用探测序列，有可能其计算的时间成本过高，导致哈希表的处理性能降低

③由于记录是存放在桶数组中的，而桶数组必然存在空槽，所以当记录本身尺寸（size）很大并且记录总数规模很大时，空槽占用的空间会导致明显的内存浪费

④删除记录时，比较麻烦。比如需要删除记录a，记录b是在a之后插入桶数组的，但是和记录a有冲突，是通过探测序列再次跳转找到的地址，所以如果直接删除a，a的位置变为空槽，而空槽是查询记录失败的终止条件，这样会导致记录b在a的位置重新插入数据前不可见，所以不能直接删除a，而是设置删除标记。这就需要额外的空间和操作。

 

2. 再散列函数法

H_i=RH_i(key), i=1,2,…,k RH_i均是不同的散列函数（比如除留余数、折叠、平方取中），在同义词产生地址冲突时就换用另一个散列函数计算散列地址，直到碰撞不再发生。

优点：不易产生“聚集”。

缺点：增加了计算时间。

3. 链地址法

将所有关键字为同义词的记录存储在一个单链表中，称这种表为同义词子表，在散列表中只存储所有同义词子表的头指针。

 

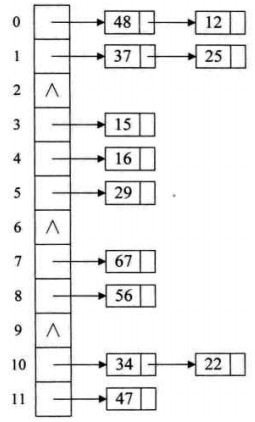
优点：

①对于记录总数频繁可变的情况，处理的比较好（也就是避免了动态调整的开销）

②由于记录存储在结点中，而结点是动态分配，不会造成内存的浪费，所以尤其适合那种记录本身尺寸（size）很大的情况，因为此时指针的开销可以忽略不计了

③删除记录时，比较方便，直接通过指针操作即可

缺点：

①存储的记录是随机分布在内存中的，这样在查询记录时，相比结构紧凑的数据类型（比如数组），哈希表的跳转访问会带来额外的时间开销

②如果所有的 key-value 对是可以提前预知，并之后不会发生变化时（即不允许插入和删除），可以人为创建一个不会产生冲突的完美哈希函数（perfect hash function），此时封闭散列的性能将远高于开放散列

 

相对于开放定址法的优点：

①拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；
②由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；
③开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间；
④在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表，删除结点不能简单地将被删结 点的空间置为空，否则将截断在它之后填人散列表的同义词结点的查找路径。这是因为各种开放地址法中，空地址单元(即开放地址)都是查找失败的条件。因此在 用开放地址法处理冲突的散列表上执行删除操作，只能在被删结点上做删除标记，而不能真正删除结点。

相对于开放定址法的缺点：

指针需要额外的空间，故当结点规模较小时，开放定址法较为节省空间，而若将节省的指针空间用来扩大散列表的规模，可使装填因子变小，这又减少了开放定址法中的冲突，从而提高平均查找速度。

 

总结：

元素少，用开放定址，冲突少，速度快；元素多，用链地址。

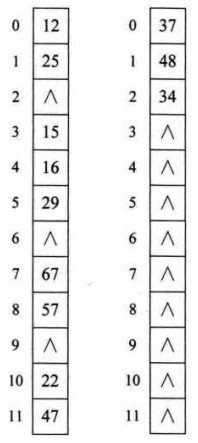
4. 公共溢出区法

为所有冲突的关键字记录建立一个公共的溢出区来存放。在查找时，对给定关键字通过散列函数计算出散列地址后，先与基本表的相应位置进行比对，如果相等，则查找成功；如果不相等，则到溢出表进行顺序查找。如果相对于基本表而言，在有冲突的数据很少的情况下，公共溢出区的结构对查找性能来说还是非常高的。