密码工程-扩展欧几里得算法

#include <stdio.h>

//这里用了int类型，所支持的整数范围较小且本程序仅支持非负整数，可能缺乏实际用途，仅供演示。
struct EX_GCD { //s,t是裴蜀等式中的系数，gcd是a,b的最大公约数
    int s;
    int t;
    int gcd;
};

struct EX_GCD extended_euclidean(int a, int b) {
    struct EX_GCD ex_gcd;
    if (b == 0) { //b等于0时直接结束求解
        ex_gcd.s = 1;
        ex_gcd.t = 0;
        ex_gcd.gcd = 0;
        return ex_gcd;
    }
    int old_r = a, r = b;
    int old_s = 1, s = 0;
    int old_t = 0, t = 1;
    while (r != 0) { //按扩展欧几里得算法进行循环
        int q = old_r / r;
        int temp = old_r;
        old_r = r;
        r = temp - q * r;
        temp = old_s;
        old_s = s;
        s = temp - q * s;
        temp = old_t;
        old_t = t;
        t = temp - q * t;
    }
    ex_gcd.s = old_s;
    ex_gcd.t = old_t;
    ex_gcd.gcd = old_r;
    return ex_gcd;
    }

int main(void) {
    int a, b;
    printf("Please input two integers divided by a space.\n");
    scanf("%d%d", &a, &b);
    if (a < b) { //如果a小于b，则交换a和b以便后续求解
        int temp = a;
        a = b;
        b = temp;
    }
    struct EX_GCD solution = extended_euclidean(a, b);
    printf("%d*%d+%d*%d=%d\n", solution.s, a, solution.t, b, solution.gcd);
    
    return 0;
}

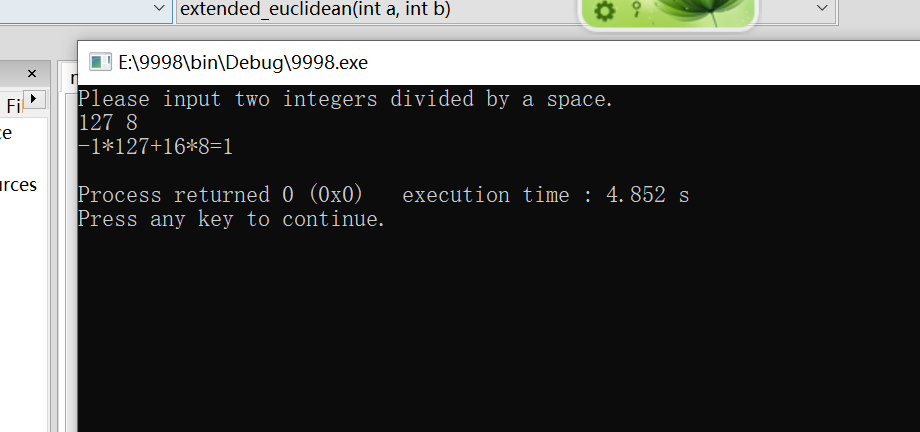
华为云实现：

 

 

计算74模167的逆 

 

 

 

 可知是79