CSAPP 并发编程

前置知识
进程
逻辑控制流(简称逻辑流) CSAPP P508: 一系列的程序计数器PC的值唯一地对应于包含在程序的可执目标文件中的指令或包含在运行时动态链接到程序的共享对象指令。这个PC值的序列叫逻辑控制流。
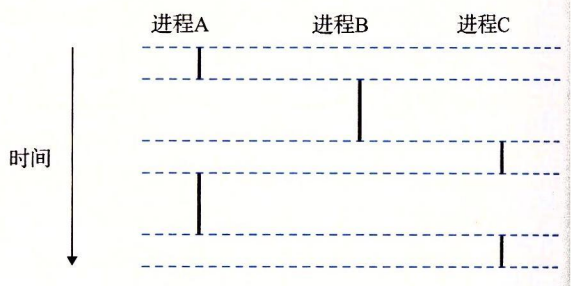
一个逻辑流的执行在时间上与另一个流重叠,称为并发流,这两个流被称为并发地运行。多个流并发地执行的现象也称为并发。
上图的关键点在于进程是轮流使用处理器的。每个进程执行它的流的一部分,然后被抢占(preempted)(暂时挂起),然后轮到其他进程。
并行流是并发流的真子集。如果两个流并发地运行在不同的处理器核或计算机上,那么我们称它们为并行流,这两个流被称为并行地运行。多个流并行地执行的现象也称为并行
系统中的每个程序都运行在某个进程的上下文中。上下文是由程序正确运行所需的状态组成的,这个状态包括存放在内存中的代码和数据,它的栈,通用目的寄存器,程序计数器,环境变量,打开文件描述符的集合。
当若干程序运行在同一个上下文下,依旧可以是同一个进程。即不一定要一个程序开一个进程。
进程提供给应用程序的关键抽象:
- 一个独立的逻辑控制流
- 一个私有的地址空间
进程是按照严格的父子层来组织的,如:父进程调用fork函数创建新的进程,这个进程被称为子进程。
子进程和父进程并不是对等的,具体可体现在:父进程可以杀死子进程,但是子进程杀不死父进程;父进程可以等待子进程,但是子进程并不会等待父进程。
信号:一种更高层的软件形式的异常,称为Linux信号,允许进程或内核中断其他进程。
一个发出而没有被接收的信号叫做待处理信号(pending signal)。在任何时刻,一种类型至多只会有一个待处理信号。如果一个进程有一个类型为上的待处理信号,那么任何接下来发送到这个进程的类型为左的信号都不会排队等待;它们只是被简单地丢弃。
内核为每个进程在 pending 位向量中维护着待处理信号的集合。只要传送了一个类型为 k 的信号,内核就会设置 pending 中的第 k 位。
个进程可以有选择性地阻塞接收某种信号。当一种信号被阻塞时,它仍可以被发送,但是产生的待处理信号不会被接收,直到进程取消对这种信号的阻塞
内核为每个进程在blocked位向量中维护着被阻塞的信号集合。
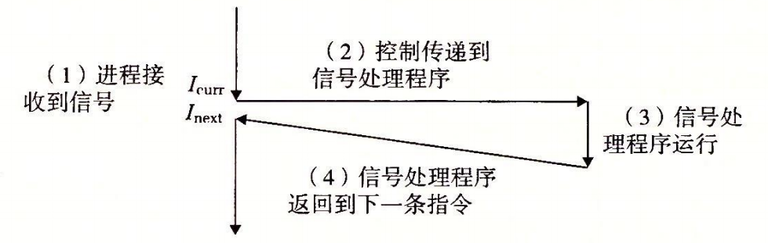
当内核把进程 p 从内核模式切换到用户模式时(例如,从系统调用返回或是完成了一次上下文切换),它会检查进程 p 的未被阻塞的待处理信号的集合(pending &~blocked)。
如果这个集合为空(通常情况下),那么内核将控制传递到 p 的逻辑控制流中的下一条指令。
然而,如果集合是非空的,那么内核选择集合中的某个信号 k (通常是最小的 k),并且强制 p 接收信号 k。收到这个信号会触发进程采取某种行为。一旦进程完成了这个行为,那么控制就传递回 p 的逻辑控制流中的下一条指令
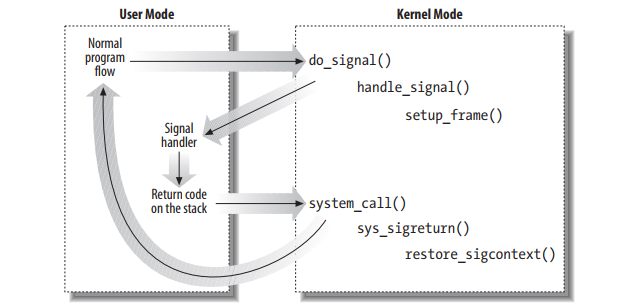
Linux 为每个进程维护了一个单独的虚拟地址空间
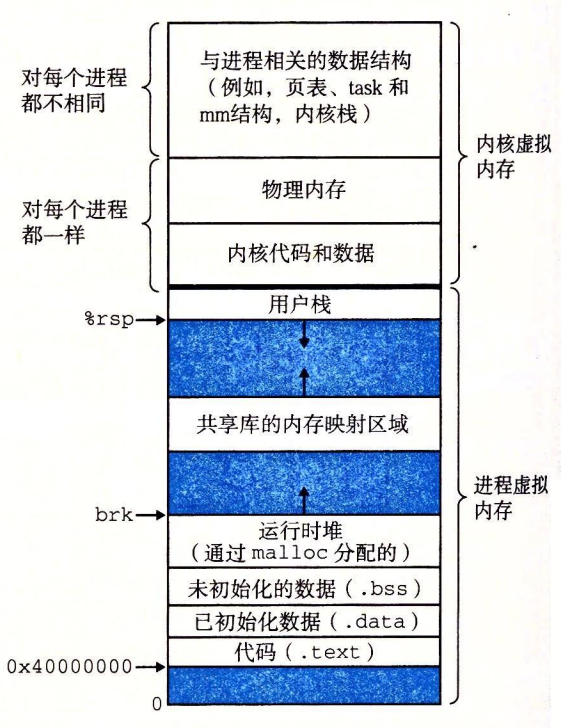
内核虚拟内存包含内核中的代码和数据结构。内核虚拟内存的某些区域被映射到所有进程共享的物理页面。(某些区域其实就是上图的物理内存,内核代码和数据)
有趣的是,Linux 也将一组连续的虚拟页面(大小等于系统中 DRAM 的总量)映射到相应的一组连续的物理页面。这就为内核提供了一种便利的方法来访问物理内存中任何特定的位置(如设备使用MMIO时)
内核虚拟内存的其他区域包含每个进程都不相同的数据。比如说,页表、内核在进程的上下文中执行代码时使用的栈,以及记录虚拟地址空间当前组织的各种数据结构。
内核为系统中的每个进程维护一个单独的任务结构(源代码中的 task_struct)。
任务结构中的元素包含或者指向内核运行该进程所需要的所有信息(例如,PID、指向用户栈的指针、可执行目标文件的名字,以及程序计数器)。
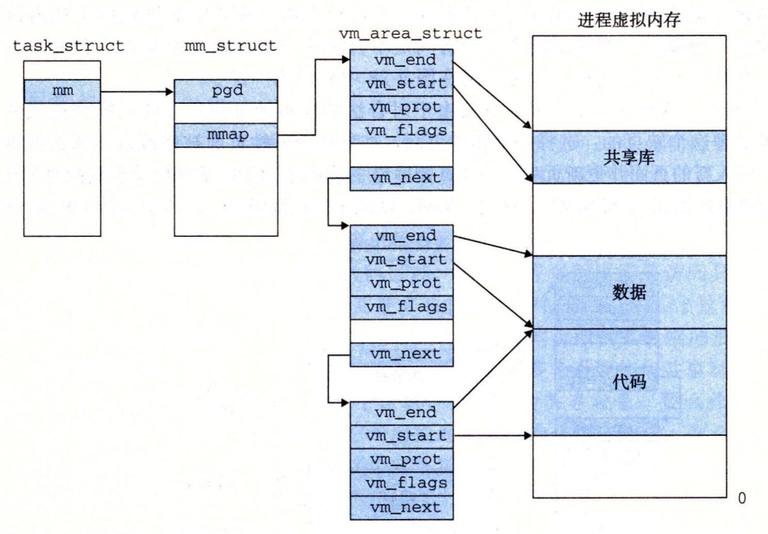
任务结构中的一个条目指向 mm_struct,它描述了虚拟内存的当前状态。
- 其中 pgd 指向第一级页表(页全局目录)的基址
- mmap 指向一个 vm_area_structs(区域结构)的链表,其中每个 vm_area_structs 都描述了当前虚拟地址空间的一个区域。当内核运行这个进程时,就将 pgd 存放在 CR3 控制寄存器中。
Linux 将虚拟内存组织成一些区域(也叫做段)的集合。一个区域(area)就是已经存在着的(已分配的)虚拟内存的连续片(chunk),这些页是以某种方式相关联的。例如,代码段、数据段、堆、共享库段,以及用户栈都是不同的区域。
每个存在的虚拟页面都保存在某个区域中,而不属于某个区域的虚拟页是不存在的,并且不能被进程引用。
所以要注意区别下页表和vm_area_struct作用的区别。
页表的作用简单来说是将VA转化为PA。
依据"每个存在的虚拟页面都保存在某个区域中,而不属于某个区域的虚拟页是不存在的,并且不能被进程引用。"的特性,vm_area_struct的作用可以进行缺页异常处理:
线程
基于进程的并发编程和基于 I/O 多路复用的并发编程
- 基于进程的并发编程
构造并发程序最简单的方法就是用进程,使用那些大家都很熟悉的函数,像 fork、exec 和 waitpid。
对于在父、子进程间共享状态信息,进程有一个非常清晰的模型:共享文件表,但是不共享用户地址空间。进程有独立的地址空间既是优点也是缺点。
另一方面,独立的地址空间使得进程共享状态信息变得更加困难。为了共享信息,它们必须使用显式的 IPC(进程间通信)机制。
Unix IPC:第 8 章中的 waitpid 函数和信号是基本的 IPC 机制,它们允许进程发送小消息到同一主机上的其他进程。第 11 章的套接字接口是 IPC 的一种重要形式,它允许不同主机上的进程交换任意的字节流。
- 基于 I/O 多路复用的并发编程
I/O 多路复用(I/O multiplexing)技术。基本的思路就是使用 select 函数,要求内核挂起进程,只有在一个或多个I/O 事件发生后,才将控制返回给应用程序
一个基于 I/O 多路复用是运行在单一进程上下文中的,因此每个逻辑流都能访问该进程的全部地址空间。这使得在流之间共享数据变得很容易。但是明显缺点是不能充分利用多核处理器。只要某个逻辑流正忙于读一个文本行,其他逻辑流就不可能有进展。
基于线程的并发编程
线程定义和特性
线程(thread)就是运行在进程上下文中的逻辑流。在本书里迄今为止,程序都是由每个进程中一个线程组成的。但是现代系统也允许我们编写一个进程里同时运行多个线程的程序。
线程由内核自动调度。每个线程都有它自己的线程上下文(thread context),包括一个唯一的整数线程 ID(Thread ID,TID)、栈、栈指针、程序计数器、通用目的寄存器和条件码。所有的运行在一个进程里的线程共享该进程的整个虚拟地址空间。
基于线程的逻辑流结合了基于进程和基于 I/O 多路复用的流的特性:
-
同进程一样,线程由内核自动调度,并且内核通过一个整数 ID 来识别线程。
-
同基于 I/O 多路复用的流一样,多个线程运行在单一进程的上下文中,因此共享这个进程虚拟地址空间的所有内容,包括它的代码、数据、堆、共享库和打开的文件。
多线程的执行模型在某些方面和多进程的执行模型是相似的。但是线程不像进程那样,不是按照严格的父子层次来组织的。和一个进程相关的线程组成一个对等(线程)池,独立于其他线程创建的线程。
主线程和其他线程的区别仅在于它总是进程中第一个运行的线程。对等(线程)池概念的主要影响是,一个线程可以杀死它的任何对等线程,或者等待它的任意对等线程终止。另外,每个对等线程都能读写相同的共享数据。
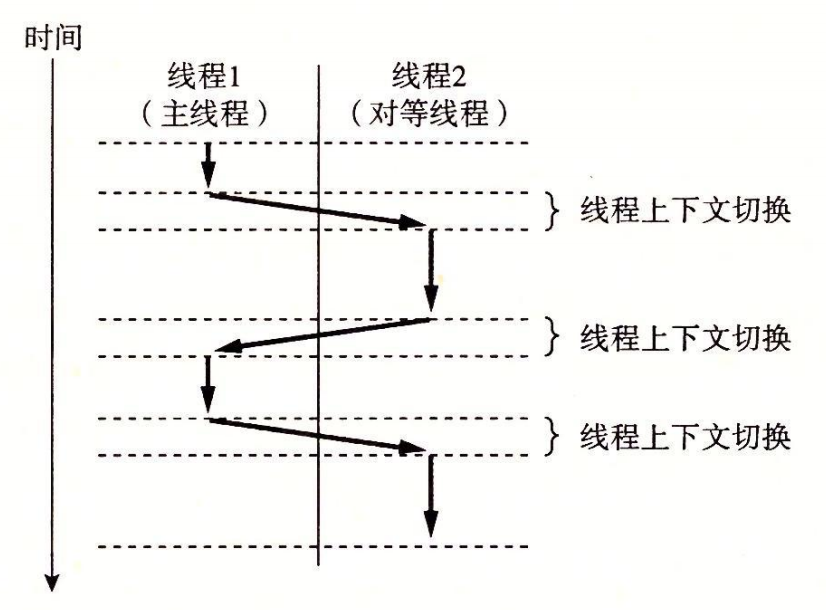
线程内存模型
一组并发线程运行在一个进程的上下文中,对于各个线程来说
-
自己独立的上下文有:线程 ID、栈、栈指针、程序计数器、条件码和通用目的寄存器值。每个线程和其他线程一起共享进程上下文的剩余部分。
-
共享进程的上下文有:整个用户虚拟地址空间,它是由只读文本(代码)、读/写数据、堆以及所有的共享库代码和数据区域组成的。线程也共享相同的打开文件的集合。
如让一个线程去读或写另一个线程的寄存器值是不可能的。但是如果某个线程修改了一个内存位置,那么其他每个线程最终都能在它读这个位置时发现这个变化。
多线程的 C 程序中变量根据它们的存储类型被映射到虚拟内存:
-
全局变量。全局变量是定义在函数之外的变量。在运行时,虚拟内存的读/写区域只包含每个全局变量的一个实例,任何线程都可以引用。
-
本地静态变量。本地静态变量是定义在函数内部并有 static 属性的变量。和全局变量一样,虚拟内存的读/写区域只包含在程序中声明的每个本地静态变量的一个实例。
可以理解为本地静态变量为作用域只位于函数内的全局变量。
-
本地自动变量。本地自动变量就是定义在函数内部但是没有 static 属性的变量。在运行时,每个线程的栈都包含它自己的所有本地自动变量的实例。即使多个线程执行同一个线程例程时也是如此。
Posix线程API 和 Posix信号量
对于其中一个API我想说明一下:
pthread_once 函数允许你初始化与线程例程相关的状态。
#include <pthread.h>
pthread_once_t once_control = PTHREAD_ONCE_INIT;
int pthread_once(pthread_once_t *once_control,
void (*init_routine)(void));
once_control 变量是一个全局或者静态变量,总是被初始化为 PTHREAD_ONCE_INIT。当你第一次用参数 once_control 调用 pthread_once 时,它调用 init_routine,这是一个没有输入参数、也不返回什么的函数。接下来的以 once_control 为参数的 pthread_once 调用不做任何事情。
注意这个once_control 变量名字我们可以任意取,变成flag,ifonce等等都行。
注意是第一次用参数once_control 调用 pthread_once 时,会调用 init_routine 执行一次初始化操作,再用就不进行初始化了!
实际实现
psum
#include "csapp.h"
long nelems_per_thread;
long *sum_per_thread;
double cpu_time_used;
void *psum_thread(void *vargp)
{
long idx = *(long *)vargp;
long start = idx * nelems_per_thread;
long end = start + nelems_per_thread;
long localsum = 0;
for (long i = start; i < end; i++) localsum += i;
sum_per_thread[idx] = localsum;
return NULL;
}
/*
* 并行地对一列整数 0,⋯,n−1求和
* 传入参数为nelems 和 nthreads,要求nelems是nthreads的倍数。
*/
void psum(long nelems, long nthreads)
{
nelems_per_thread = nelems / nthreads;
sum_per_thread = (long *)malloc(sizeof(long) * nthreads);
long *idxArr = (long *)malloc(sizeof(long) * nthreads);
pthread_t *pthreadIdArr = (pthread_t *)malloc(sizeof(pthread_t) * nthreads);
long sum = 0, rightSum = (nelems - 1) * nelems / 2;
struct timeval start, end;
long seconds, useconds;
double total_time;
gettimeofday(&start, NULL); // 开始计时
for (long i = 0; i < nthreads; i++) {
idxArr[i] = i;
Pthread_create(&pthreadIdArr[i], NULL, psum_thread, &idxArr[i]);
}
for (long i = 0; i < nthreads; i++) Pthread_join(pthreadIdArr[i], NULL);
gettimeofday(&end, NULL); // 结束计时
seconds = end.tv_sec - start.tv_sec;
useconds = end.tv_usec - start.tv_usec;
total_time = seconds + useconds / 1e6;
for (long i = 0; i < nthreads; i++) {
printf("sum_per_thread[%ld]: %ld\n", i, sum_per_thread[i]);
sum += sum_per_thread[i];
}
if (sum != rightSum) printf("Threads sum Error:");
else printf("Threads sum Success:");
printf("\nsum: %ld vs rightSum: %ld\n",sum, rightSum);
printf("nelems:%ld nthreads:%ld time: %lf seconds\n", nelems, nthreads, total_time);
}
int main(int argc, char **argv)
{
assert(argc > 1);
if (strcmp(argv[1], "psum") == 0){
assert(argc > 3);
long nelems = (1L << atoi(argv[2]));
long nthreads = atoi(argv[3]);
psum(nelems, nthreads);
}
return 0;
}
时间打印出来确实有点像CSAPP下面的这幅图:
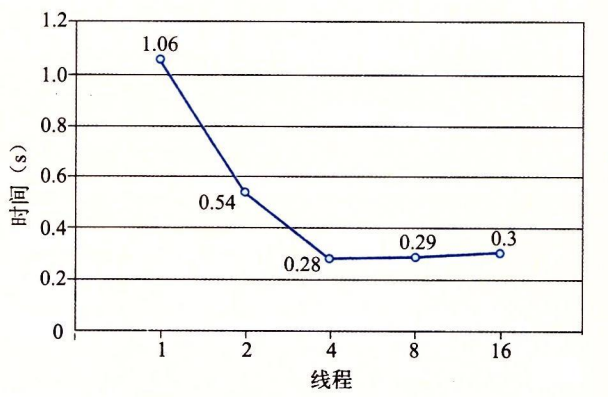
为何线程变多后运行时间还会变多呢?可能是如下原因:
这是由于在一个核上多个线程上下文切换的开销。由于这个原因,并行程序常常被写为每个核上只运行一个线程。
PLCS
总得来说这道题目的思考解决方法为:
Brent's Theorem
布伦特定理(Brent's Theorem),又称为工作-深度定理,是并行计算中的一个重要理论。它描述了并行算法中总工作量、计算深度和可用处理器数量之间的关系。该定理由理查德·布伦特(Richard Brent)于1974年提出。
对于一个并行计算:
- 设 \(T_1\) 为总工作量(即单个处理器完成整个计算所需的时间)。
- 设 \(T_\infty\) 为计算深度(即使用无限处理器时的计算时间,也称为最长的顺序依赖路径)。
- 设 \(P\) 为可用处理器的数量。
计算在 \(P\) 个处理器上的运行时间 \(T_P\) 满足以下不等式:
\( \frac{T_1}{P} \leq T_P \leq \frac{T_1}{P} + T_\infty \)

- 阿姆达尔定律(Amdahl's Law)与布伦特定理互为补充,描述了计算中的顺序部分对加速比的限制。
- 布伦特定理为并行算法的设计和分析提供了实际指导,突出工作量、计算深度和处理器数量之间的权衡关系。
一个性能极差的实现
/*
* 并行地求最长公共子序列
* 传入参数为字符串A和B,以及线程数nthreads
*/
#define CELL_MAX 20004
#define STRLEN_MAX 10004
#define THREADNUM_MAX 18
struct {
int y;
int x;
} cellLine[CELL_MAX];
int cellCount = 0;
int dp[STRLEN_MAX][STRLEN_MAX];
typedef struct {
int sta;
int fin;
} cellRange;
const char *strA;
const char *strB;
void *plcs_thread(void *vargp)
{
cellRange cell_range_thread = *(cellRange *)vargp;
int sta = cell_range_thread.sta;
int fin = cell_range_thread.fin;
int y, x;
while (sta <= fin) {
y = cellLine[sta].y; x = cellLine[sta].x;
if (strB[y - 1] == strA[x - 1]) dp[y][x] = dp[y - 1][x - 1] + 1;
else dp[y][x] = dp[y - 1][x] > dp[y][x - 1] ? dp[y - 1][x] : dp[y][x - 1];
sta++;
}
return NULL;
}
int plcs(char *A, char *B, int nthreads)
{
strA = A; strB = B;
int lenA = strlen(A);
int lenB = strlen(B);
int roundMax = lenA + lenB - 1;
pthread_t pthreadIds[THREADNUM_MAX];
cellRange cell_range_threads[THREADNUM_MAX];
//初始化
for (int i = 0; i <= lenA; i++) dp[0][i] = 0;
for (int i = 0; i <= lenB; i++) dp[i][0] = 0;
cellLine[cellCount].y = 1; cellLine[cellCount].x = 1; cellCount++;
// 开始计时
struct timeval start, end;
long seconds, useconds;
double total_time;
gettimeofday(&start, NULL);
// 并行计算
for (int round = 0; round < roundMax; round++) {
// 将任务分配给线程执行
int sta, fin, cell_per_thread_num;
if (cellCount <= nthreads) cell_per_thread_num = 1;
else cell_per_thread_num = cellCount / nthreads;
for (int i = 0; i < nthreads; i++) {
sta = i * cell_per_thread_num; fin = sta + cell_per_thread_num - 1;
if (i == nthreads - 1) fin = cellCount - 1;
cell_range_threads[i].sta = sta;
cell_range_threads[i].fin = fin;
Pthread_create(&pthreadIds[i], NULL, plcs_thread, &cell_range_threads[i]);
}
// 等待线程执行完毕
for (int i = 0; i < nthreads; i++) Pthread_join(pthreadIds[i], NULL);
//计算出下一轮能够并行计算的单元格
int t_cellCount = 0, ny, nx, y, x;
for (int cellidx = 0; cellidx < cellCount; cellidx++) {
y = cellLine[cellidx].y; x = cellLine[cellidx].x;
ny = y + 1;
nx = x;
if (ny <= lenB) {
cellLine[t_cellCount].y = ny;
cellLine[t_cellCount].x = nx;
t_cellCount++;
}
if (cellidx == cellCount - 1){
ny = y;
nx = x + 1;
if (nx <= lenA) {
cellLine[t_cellCount].y = ny;
cellLine[t_cellCount].x = nx;
t_cellCount++;
}
}
}
cellCount = t_cellCount;
}
// 结束计时
gettimeofday(&end, NULL);
seconds = end.tv_sec - start.tv_sec;
useconds = end.tv_usec - start.tv_usec;
total_time = seconds + useconds / 1e6;
printf("Threads: %d and PLCS time: %lf seconds\n", nthreads, total_time);
return dp[lenB][lenA];
}
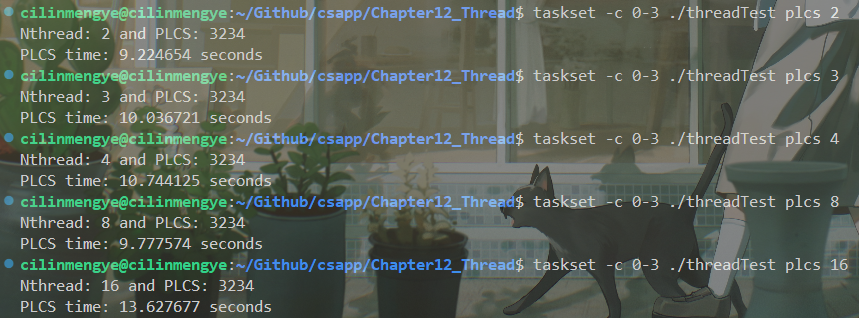
上述代码正确性可以保证,能够正确求出LCS,但是性能实在堪忧,在两个字符串都是10000长度的情况下,普通LCS和基于线实现的PLCS运行时间如下:

简直没眼看了
一个我自认为改进得不错的写法
void *plcs_thread(void *vargp)
{
cellRange cellRangeThread = *(cellRange *)vargp;
int stay = cellRangeThread.sta.y; int stax = cellRangeThread.sta.x;
int finy = cellRangeThread.fin.y;
while (stay >= finy) {
if (strB[stay - 1] == strA[stax - 1]) dp[stay][stax] = dp[stay - 1][stax - 1] + 1;
else dp[stay][stax] = dp[stay - 1][stax] > dp[stay][stax - 1] ? dp[stay - 1][stax] : dp[stay][stax- 1];
stay--; stax++;
}
return NULL;
}
int plcs(char *A, char *B, int nthreads)
{
strA = A; strB = B;
int lenA = strlen(A); int lenB = strlen(B);
int roundMax = lenA + lenB - 1, i, round;
pthread_t pthreadIds[THREADNUM_MAX];
cellRange cellRangeThreads[THREADNUM_MAX];
//初始化
for (i = 0; i <= lenA; i++) dp[0][i] = 0;
for (i = 0; i <= lenB; i++) dp[i][0] = 0;
cell dw, tp; // 右对角线上底点和顶点
dw.y = 1, dw.x = 1;
tp.y = 1, tp.x = 1;
// 开始计时
struct timeval start, end;
long seconds, useconds;
double total_time;
gettimeofday(&start, NULL);
// 并行计算
int cellCount, threadNum, cellPerThread;
int stay, stax, finy, finx;
for (round = 0; round < roundMax; round++) {
// 将任务分配给线程执行
//assert((dw.y - tp.y) == (tp.x - dw.x));
cellCount = dw.y - tp.y + 1; // 本轮需要计算的单元格数量
threadNum = nthreads; // 真正需要用到的线程数
cellPerThread = cellCount / nthreads; // 每个线程需要计算的单元格数
// 性能瓶颈1:线程的开销和竞争,需要设置合理的线程数。
if (cellPerThread < CELLPERTHREAD_MIN) { // 当每个线程计算的单元格数太少就没有意义了。
threadNum = cellCount / CELLPERTHREAD_MIN; // 合理需要的线程数。
if (threadNum <= 0) { // 说明本来需要计算的单元格数太少,少于CELLPERTHREAD_MIN,那么交给一个线程进行计算就行了。
threadNum = 1;
cellPerThread = cellCount;
} else cellPerThread = CELLPERTHREAD_MIN; // 说明这轮需要计算的单元数起码大于CELLPERTHREAD_MIN
}
for (i = 0; i < threadNum; i++) {
stay = dw.y - i * cellPerThread; stax = dw.x + i * cellPerThread;
finy = stay - cellPerThread + 1; finx = stax + cellPerThread - 1;
if (i == threadNum - 1) { // 处理cellCount和nthreads(或者是CELLPERTHREAD_MIN)非倍数关系时的情况。
finy = tp.y;
finx = tp.x;
}
cellRangeThreads[i].sta.y = stay; cellRangeThreads[i].sta.x = stax;
cellRangeThreads[i].fin.y = finy; cellRangeThreads[i].fin.x = finx;
Pthread_create(&pthreadIds[i], NULL, plcs_thread, &cellRangeThreads[i]);
}
// 等待线程执行完毕
for (i = 0; i < threadNum; i++) Pthread_join(pthreadIds[i], NULL);
// 计算出下一轮能够并行计算的单元格, 即计算出单元格所在的对角线。
// 性能瓶颈2: 合理地得出需要计算的单元格
if (dw.y + 1 <= lenB) dw.y += 1, dw.x = dw.x;
else dw.y = lenB, dw.x += 1;
if (tp.x + 1 <= lenA) tp.y = tp.y, tp.x += 1;
else tp.y += 1, tp.x = lenA;
}
// 结束计时
gettimeofday(&end, NULL);
seconds = end.tv_sec - start.tv_sec;
useconds = end.tv_usec - start.tv_usec;
total_time = seconds + useconds / 1e6;
printf("Threads: %d and PLCS time: %lf seconds\n", nthreads, total_time);
return dp[lenB][lenA];
}
总得来说,相较于前一种写法,我改进后省去每轮需要保存每个单元格的操作。并且对于每轮若总单元格需要计算的量少的话会动态线程数,避免线程开销比计算开销还大。
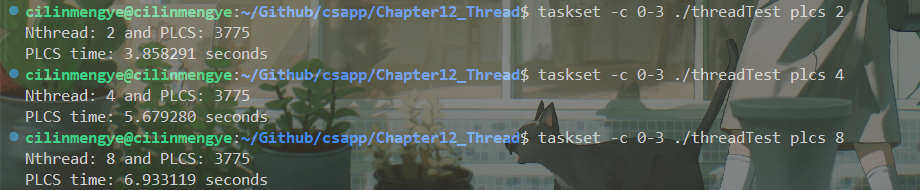
然后好像并没有什么进步:

但是如果将线程数开到2,有点进步,且相较于上个版本开2个线程效果好多了:

但是后面线程数开多后反而退步了。
进一步的改进
我觉得我大方向错误了,以下为搜集的资料,日后再解决:
我回来了,果然大方向错误了,我上述代码有明显的问题就是我对每个对角线都开了T个线程进行计算。本来要求只能用T个进程,现在我总共使用了\(T * round\)个线程...
现在优化的方向就清楚了:
- 在
main函数中预处理出每一轮round,每一个线程需要计算的单元格范围 - 对
T == 1的情况特殊处理,因为main函数中有预处理,这些预处理对T == 1是不必要的 - 开T个线程,每个线程执行如下伪代码:
但是现在有可能会发生如下情况:一个线程\(i\)运行到\(round_k\),而另一个线程\(j\)已经运行到\(round_{k+1}\), 下一次还是线程\(j\)运行,这个时候线程\(j\)的单元格计算可能需要依赖线程\(i\)在\(round_{k+1}\)中计算的单元格,所以线程\(j\)需要等待。for (int round = 0; round < 2 * n - 1; round++) { // 1. 计算出本轮能够计算的单元格 // 2. 将任务分配给线程执行 // 3. 等待线程执行完毕 }
对dp访问缓存局部性的优化,若按照普通情况访问dp是以对角线进行访问的,这个时候缓存局部性极差
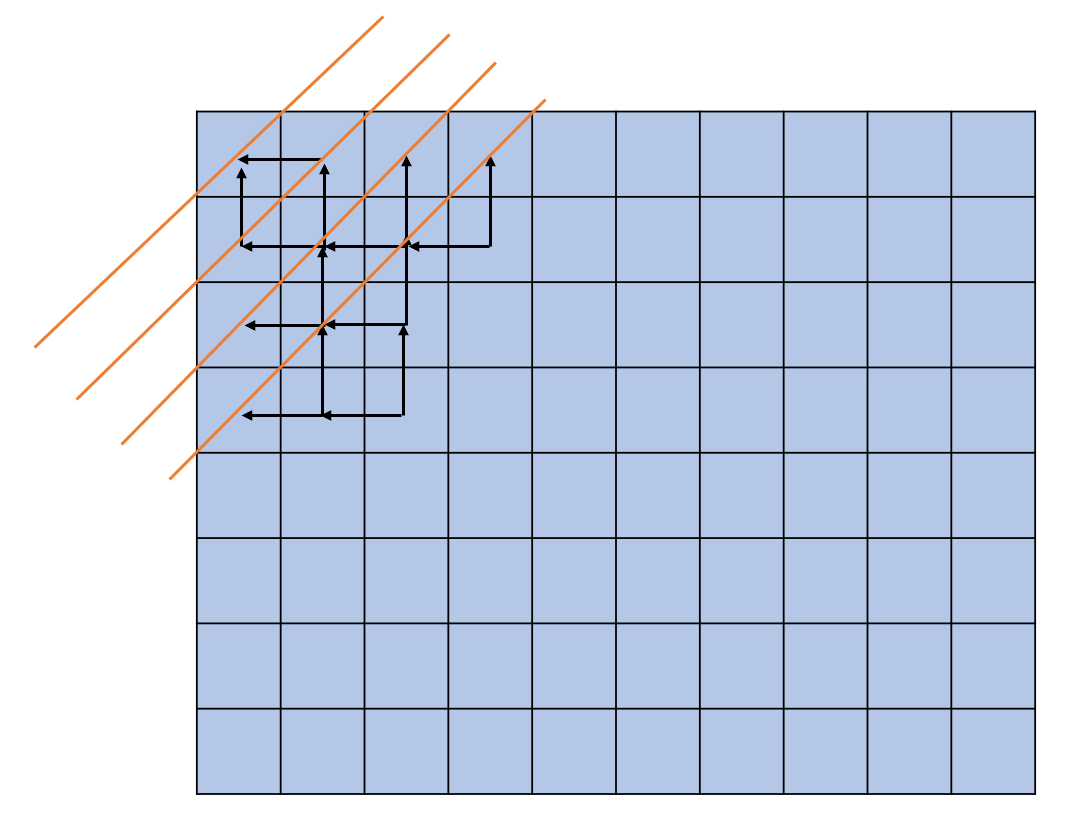
箭头指向表示依赖
那么其实可以这样旋转下就有可以以按行访问了
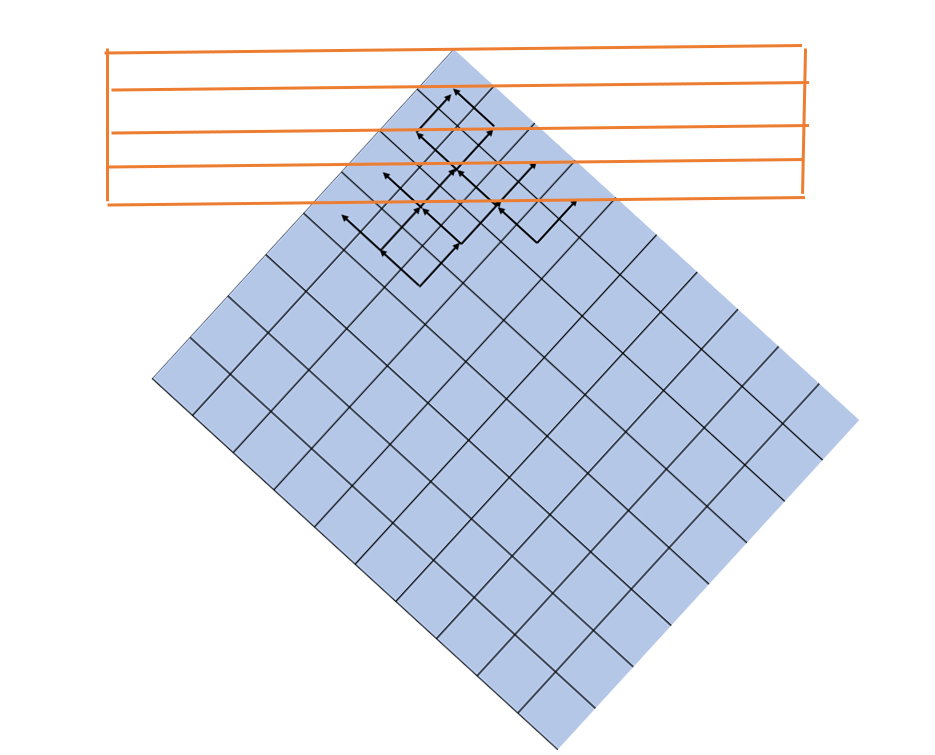
一个正确的实现,但是性能不太好
/*
* 并行地求最长公共子序列
* 传入参数为字符串A和B,以及线程数nthreads
*/
#define CELL_MAX 20004
#define STRLEN_MAX 10004
#define THREADNUM_MAX 18
const char *strA, *strB;
int roundNum, dp[STRLEN_MAX][STRLEN_MAX];
typedef struct { // 表示对角线上底点和定点
int y, x;
} cell;
struct { // 每个线程在对角线上处理单元格的开始点和结束点
cell sta, fin;
} cellRangeThreads[STRLEN_MAX + STRLEN_MAX][THREADNUM_MAX];
int roundThreadNum[STRLEN_MAX + STRLEN_MAX], T, waitThreadNum; // T值为传入的nthread,表示总的线程数
sem_t threadMutexs[THREADNUM_MAX], mutex;
//当只有一个线程就运行普通的LCS
void olcs(int lenA, int lenB)
{
for (int i = 1; i <= lenB; i++) {
for (int j = 1; j <= lenA; j++){
if (strA[j - 1] == strB[i - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i - 1][j] > dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1];
}
}
}
void *plcs_thread(void *vargp)
{
int threadId = *(int *)vargp, round, stay, stax, finy;
for (round = 0; round < roundNum; round++) {
if (threadId >= roundThreadNum[round]) { // 说明线程threadId在这轮round中未启动
P(&mutex);
//printf("thread_%d not start up in round %d and roundThreadNum[%d] is %d\n", threadId, round, round, roundThreadNum[round]);
waitThreadNum++;
if (waitThreadNum < T) {
V(&mutex);
P(&threadMutexs[threadId]);
} else {
assert(waitThreadNum == T);
for (int i = 0; i < T; i++) if (i != threadId) V(&threadMutexs[i]);
waitThreadNum = 0;
V(&mutex);
}
continue; // 直接进入下一轮round
}
// 计算单元格
stay = cellRangeThreads[round][threadId].sta.y, stax = cellRangeThreads[round][threadId].sta.x;
finy = cellRangeThreads[round][threadId].fin.y;
while (stay >= finy) {
if (strB[stay - 1] == strA[stax - 1]) dp[stay][stax] = dp[stay - 1][stax - 1] + 1;
else dp[stay][stax] = dp[stay - 1][stax] > dp[stay][stax - 1] ? dp[stay - 1][stax] : dp[stay][stax- 1];
stay--; stax++;
}
// 等待其余线程,一起进入下一轮round。
P(&mutex);
//printf("thread_%d finish in round %d\n", threadId, round);
waitThreadNum++;
if (waitThreadNum < T) {
V(&mutex);
P(&threadMutexs[threadId]);
} else {
assert(waitThreadNum == T);
for (int i = 0; i < T; i++) if (i != threadId) V(&threadMutexs[i]);
waitThreadNum = 0;
V(&mutex);
}
}
return NULL;
}
int plcs(char *A, char *B, int nthreads)
{
strA = A; strB = B;
int lenA = strlen(A); int lenB = strlen(B);
// 初始化dp的边界数值
for (int i = 0; i <= lenA; i++) dp[0][i] = 0;
for (int i = 0; i <= lenB; i++) dp[i][0] = 0;
if (nthreads == 1) {
olcs(lenA, lenB);
// for (int i = 0; i <= lenB; i++) {
// for (int j = 0; j <= lenA; j++) printf("%d ", dp[i][j]);
// printf("\n");
// }
return dp[lenB][lenA];
}
T = nthreads;
waitThreadNum = 0;
roundNum = lenA + lenB - 1;
int threadIds[THREADNUM_MAX];
pthread_t pthreadIds[THREADNUM_MAX];
// 预处理出每轮每个线程需要计算的单元格
cell dw, tp;
dw.y = 1, dw.x = 1;
tp.y = 1, tp.x = 1;
int round, stay, stax, finy, finx, cellCount, threadNum, cellPerThread;
for (round = 0; round < roundNum; round++) {
cellCount = dw.y - tp.y + 1; // 本轮需要计算的单元格数量
if (cellCount < nthreads) threadNum = cellCount; // 真正需要用到的线程数
else threadNum = nthreads;
cellPerThread = cellCount / threadNum; // 每个线程需要计算的单元格数
roundThreadNum[round] = threadNum;
for (int i = 0; i < threadNum; i++) {
stay = dw.y - i * cellPerThread; stax = dw.x + i * cellPerThread;
finy = stay - cellPerThread + 1; finx = stax + cellPerThread - 1;
if (i == threadNum - 1) { // 处理cellCount和nthreads(或者是CELLPERTHREAD_MIN)非倍数关系时的情况。
finy = tp.y;
finx = tp.x;
}
cellRangeThreads[round][i].sta.y = stay; cellRangeThreads[round][i].sta.x = stax;
cellRangeThreads[round][i].fin.y = finy; cellRangeThreads[round][i].fin.x = finx;
}
// 计算出下一轮能够并行计算的单元格, 即计算出单元格所在的对角线。
if (dw.y + 1 <= lenB) dw.y += 1, dw.x = dw.x;
else dw.y = lenB, dw.x += 1;
if (tp.x + 1 <= lenA) tp.y = tp.y, tp.x += 1;
else tp.y += 1, tp.x = lenA;
}
// 初始化下信号量
for (int i = 0; i < nthreads; i++) sem_init(&threadMutexs[i], 0, 0);
sem_init(&mutex, 0, 1);
// 创建并执行线程
for (int i = 0; i < nthreads; i++) {
threadIds[i] = i;
Pthread_create(&pthreadIds[i], NULL, plcs_thread, &threadIds[i]);
}
// 等待线程执行完毕
for (int i = 0; i < nthreads; i++) Pthread_join(pthreadIds[i], NULL);
// for (int i = 0; i <= lenB; i++) {
// for (int j = 0; j <= lenA; j++) printf("%d ", dp[i][j]);
// printf("\n");
// }
return dp[lenB][lenA];
}
考虑上缓存问题,但是实现错误
/*
* 并行地求最长公共子序列
* 传入参数为字符串A和B,以及线程数nthreads
*/
#define CELL_MAX 20004
#define STRLEN_MAX 10004
#define THREADNUM_MAX 18
const char *strA, *strB;
int roundNum, dp[STRLEN_MAX][STRLEN_MAX], dpCache[STRLEN_MAX + STRLEN_MAX][STRLEN_MAX];
typedef struct { // 表示对角线上底点和定点
int y, x;
} cell;
cell roundDW[STRLEN_MAX + STRLEN_MAX];
struct { // 每个线程在对角线上处理单元格的开始点和结束点
cell sta, fin;
} cellRangeThreads[STRLEN_MAX + STRLEN_MAX][THREADNUM_MAX];
int roundThreadNum[STRLEN_MAX + STRLEN_MAX], T, waitThreadNum; // T值为传入的nthread,表示总的线程数
sem_t threadMutexs[THREADNUM_MAX], mutex;
//当只有一个线程就运行普通的LCS
void olcs(int lenA, int lenB)
{
for (int i = 1; i <= lenB; i++) {
for (int j = 1; j <= lenA; j++){
if (strA[j - 1] == strB[i - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i - 1][j] > dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1];
}
}
}
cell dpPos2CachePos(int y, int x, int round)
{
cell res;
if (y == 0 || x == 0 || round < 0) { // 这些是到原dp边界的情况,直接让其映射到dpCache的(0,0)位置,这里的值一直都是0
res.y = 0;
res.x = 0;
} else {
res.y = round + 1;
res.x = roundDW[round].y - y;
}
return res;
}
void *plcs_thread(void *vargp)
{
int threadId = *(int *)vargp, round, stay, stax, finy;
for (round = 0; round < roundNum; round++) {
if (threadId >= roundThreadNum[round]) { // 说明线程threadId在这轮round中未启动
P(&mutex);
//printf("thread_%d not start up in round %d and roundThreadNum[%d] is %d\n", threadId, round, round, roundThreadNum[round]);
waitThreadNum++;
if (waitThreadNum < T) {
V(&mutex);
P(&threadMutexs[threadId]);
} else {
assert(waitThreadNum == T);
for (int i = 0; i < T; i++) if (i != threadId) V(&threadMutexs[i]);
waitThreadNum = 0;
V(&mutex);
}
continue; // 直接进入下一轮round
}
// 计算单元格
stay = cellRangeThreads[round][threadId].sta.y, stax = cellRangeThreads[round][threadId].sta.x;
finy = cellRangeThreads[round][threadId].fin.y;
cell cachePosSource, cachePosTarget;
while (stay >= finy) {
cachePosSource = dpPos2CachePos(stay, stax, round);
if (strB[stay - 1] == strA[stax - 1]) {
cachePosTarget = dpPos2CachePos(stay - 1, stax - 1, round - 1);
dpCache[cachePosSource.y][cachePosSource.x] = dpCache[cachePosTarget.y][cachePosTarget.x] + 1;
} else {
cachePosTarget = dpPos2CachePos(stay - 1, stax, round - 1);
if (dpCache[cachePosTarget.y][cachePosTarget.x] > dpCache[cachePosSource.y][cachePosSource.x])
dpCache[cachePosSource.y][cachePosSource.x] = dpCache[cachePosTarget.y][cachePosTarget.x];
cachePosTarget = dpPos2CachePos(stay, stax - 1, round - 1);
if (dpCache[cachePosTarget.y][cachePosTarget.x] > dpCache[cachePosSource.y][cachePosSource.x])
dpCache[cachePosSource.y][cachePosSource.x] = dpCache[cachePosTarget.y][cachePosTarget.x];
}
stay--; stax++;
}
// 等待其余线程,一起进入下一轮round。
P(&mutex);
//printf("thread_%d finish in round %d\n", threadId, round);
waitThreadNum++;
if (waitThreadNum < T) {
V(&mutex);
P(&threadMutexs[threadId]);
} else {
assert(waitThreadNum == T);
for (int i = 0; i < T; i++) if (i != threadId) V(&threadMutexs[i]);
waitThreadNum = 0;
V(&mutex);
}
}
return NULL;
}
int plcs(char *A, char *B, int nthreads)
{
strA = A; strB = B;
int lenA = strlen(A); int lenB = strlen(B);
// 初始化dp的边界数值
if (nthreads == 1) {
for (int i = 0; i <= lenA; i++) dp[0][i] = 0;
for (int i = 0; i <= lenB; i++) dp[i][0] = 0;
olcs(lenA, lenB);
// for (int i = 0; i <= lenB; i++) {
// for (int j = 0; j <= lenA; j++) printf("%d ", dp[i][j]);
// printf("\n");
// }
return dp[lenB][lenA];
} else dpCache[0][0] = 0;
T = nthreads;
waitThreadNum = 0;
roundNum = lenA + lenB - 1;
int threadIds[THREADNUM_MAX];
pthread_t pthreadIds[THREADNUM_MAX];
// 预处理出每轮每个线程需要计算的单元格
cell dw, tp;
dw.y = 1, dw.x = 1;
tp.y = 1, tp.x = 1;
roundDW[0] = dw;
int round, stay, stax, finy, finx, cellCount, threadNum, cellPerThread;
for (round = 0; round < roundNum; round++) {
cellCount = dw.y - tp.y + 1; // 本轮需要计算的单元格数量
if (cellCount < nthreads) threadNum = cellCount; // 真正需要用到的线程数
else threadNum = nthreads;
cellPerThread = cellCount / threadNum; // 每个线程需要计算的单元格数
roundThreadNum[round] = threadNum;
for (int i = 0; i < threadNum; i++) {
stay = dw.y - i * cellPerThread; stax = dw.x + i * cellPerThread;
finy = stay - cellPerThread + 1; finx = stax + cellPerThread - 1;
if (i == threadNum - 1) { // 处理cellCount和nthreads(或者是CELLPERTHREAD_MIN)非倍数关系时的情况。
finy = tp.y;
finx = tp.x;
}
cellRangeThreads[round][i].sta.y = stay; cellRangeThreads[round][i].sta.x = stax;
cellRangeThreads[round][i].fin.y = finy; cellRangeThreads[round][i].fin.x = finx;
}
// 计算出下一轮能够并行计算的单元格, 即计算出单元格所在的对角线。
if (dw.y + 1 <= lenB) dw.y += 1, dw.x = dw.x;
else dw.y = lenB, dw.x += 1;
roundDW[round + 1] = dw;
if (tp.x + 1 <= lenA) tp.y = tp.y, tp.x += 1;
else tp.y += 1, tp.x = lenA;
}
// 初始化下信号量
for (int i = 0; i < nthreads; i++) sem_init(&threadMutexs[i], 0, 0);
sem_init(&mutex, 0, 1);
// 创建并执行线程
for (int i = 0; i < nthreads; i++) {
threadIds[i] = i;
Pthread_create(&pthreadIds[i], NULL, plcs_thread, &threadIds[i]);
}
// 等待线程执行完毕
for (int i = 0; i < nthreads; i++) Pthread_join(pthreadIds[i], NULL);
cell finPos = dpPos2CachePos(lenB, lenA, roundNum - 1);
// int maxj = lenA > lenB ? lenA : lenB;
// for (int i = 0; i <= roundNum; i++){
// for (int j = 0; j <= maxj; j++)
// printf("%d ", dpCache[i][j]);
// printf("\n");
// }
return dpCache[finPos.y][finPos.x];
}
提升巨大,但是得到的是错误的答案...且还是远远比普通lcs开销大。
但是我实际上去测试了一下上述链接中那位老哥的实现:
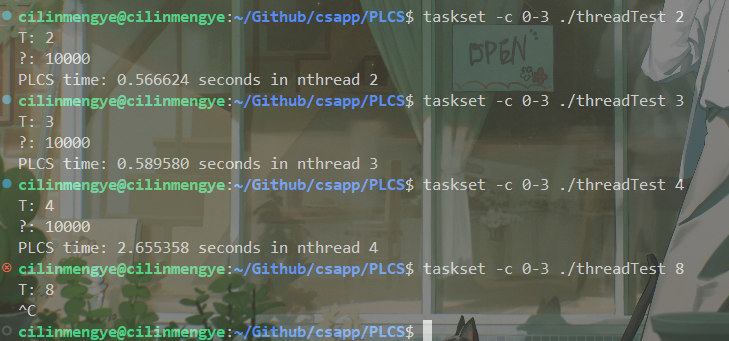
当线程数开到8以上会很慢很慢,而且也没有比当用1个线程快。不知道是我测试的方法有问题,还是plcs的实现有问题...
自旋锁
上面链接中老哥用的是自旋锁。
在并发程序中主要有三种常见的同步机制:
- 互斥锁(Mutex)
- 条件变量(Condition Variable)
- 信号量(Semaphore)。
自旋锁是锁的一种,对于自旋锁有对应的评价:
简单的笨方法可能更好 (Hill定律)---- Operating System Tree Easy Pieces P273
一般复杂意味着慢(如读者-写者锁等),某些时候简单的自旋锁反而是最有效的,因为他容易实现且高效。因此,总是优先尝试简单的笨方法。
评价一把锁从三个角度考虑:
- 正确性
- 性能
- 公平性
从性能角度,自旋锁在多处理器运行的情况下有着不错的效率。但是在单CPU上开销巨大(Operating System Tree Easy Pieces P225)


