CSAPP Data Lab

from pixiv

---

实验官方地址

环境配置

问题

当我按照官网Lab1中的WriteUp对项目进行make时，出现如下错误：

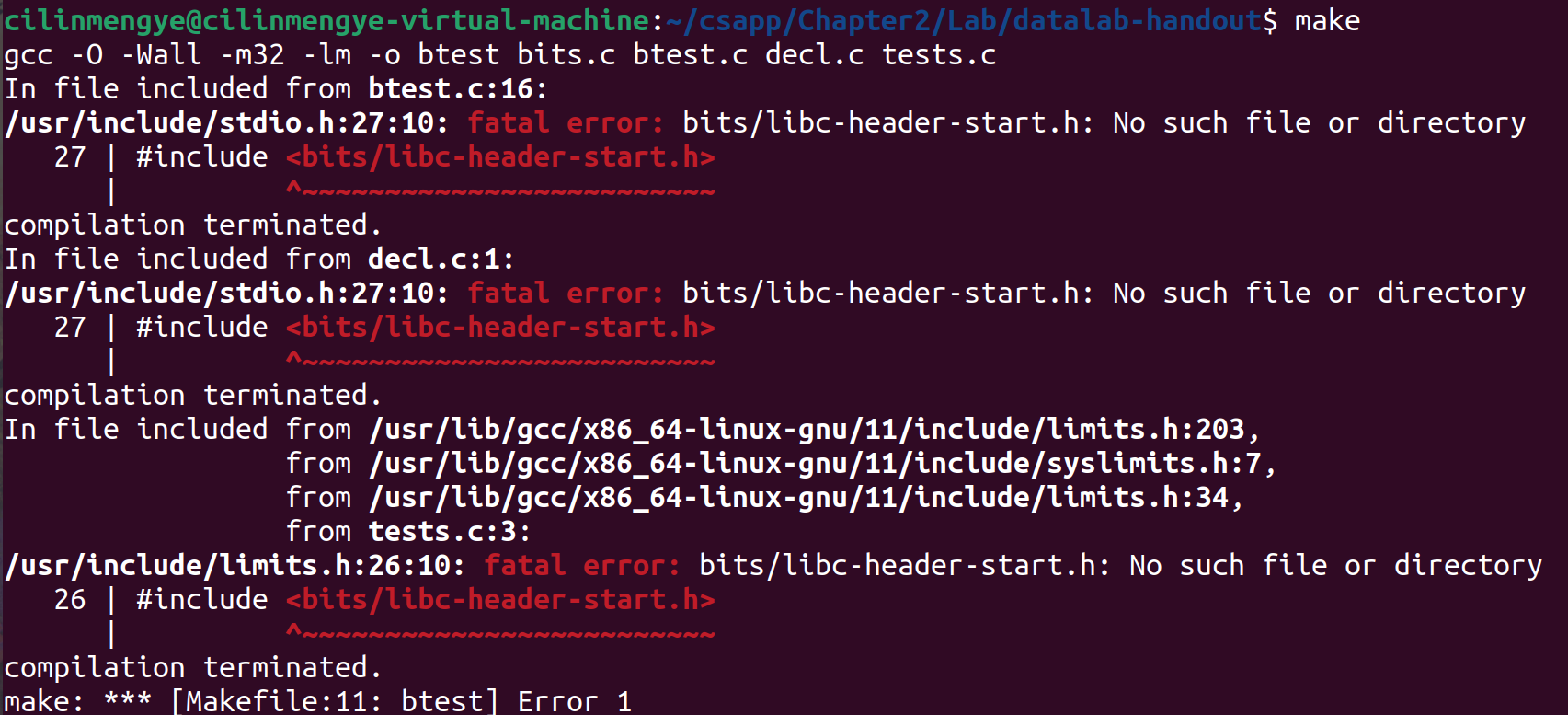
很快我找到了问题的原因：

• 
• from there

但是在apt install时又出现了问题：

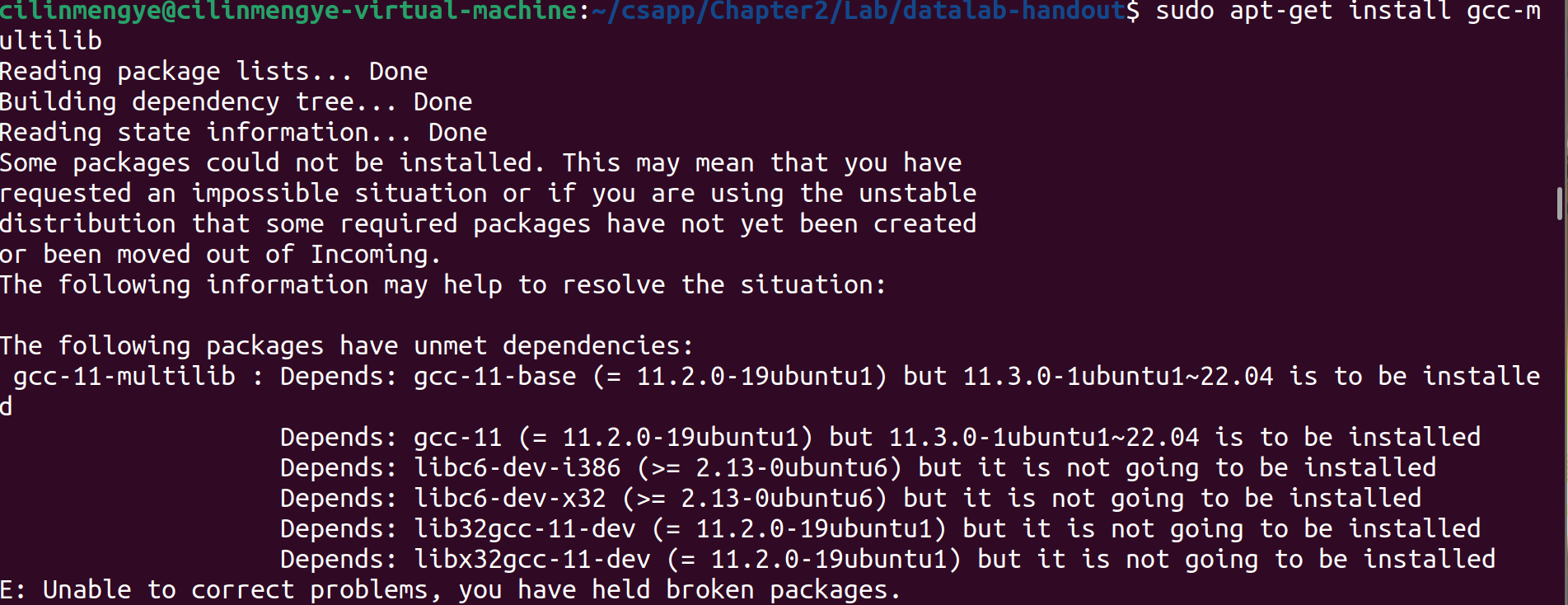
查找网络，说是Ubuntu版本太高，但是apt的源太低，要apt update

但是在apt update时又出现问题：

• 
• 解决方法
  
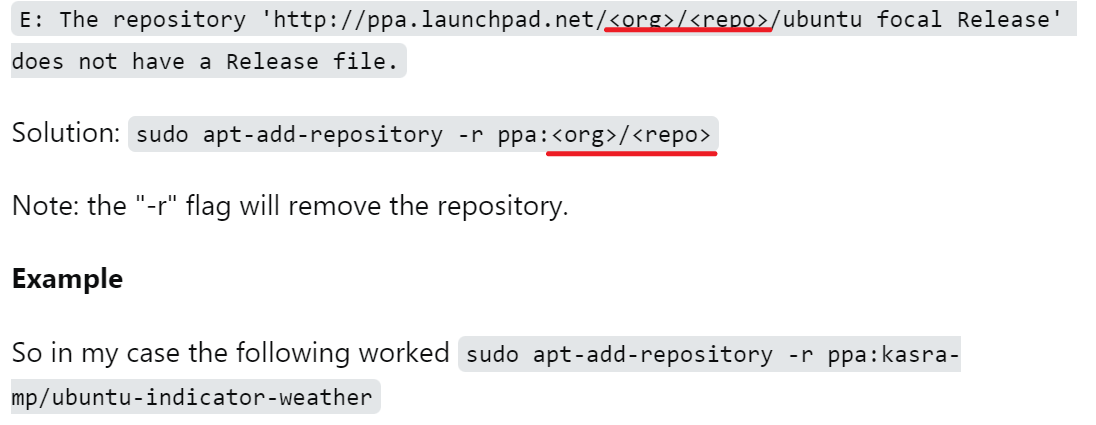
  如法炮制：
  
• apt update是成功了，但是依赖冲突问题还是有
  

最终解决方法

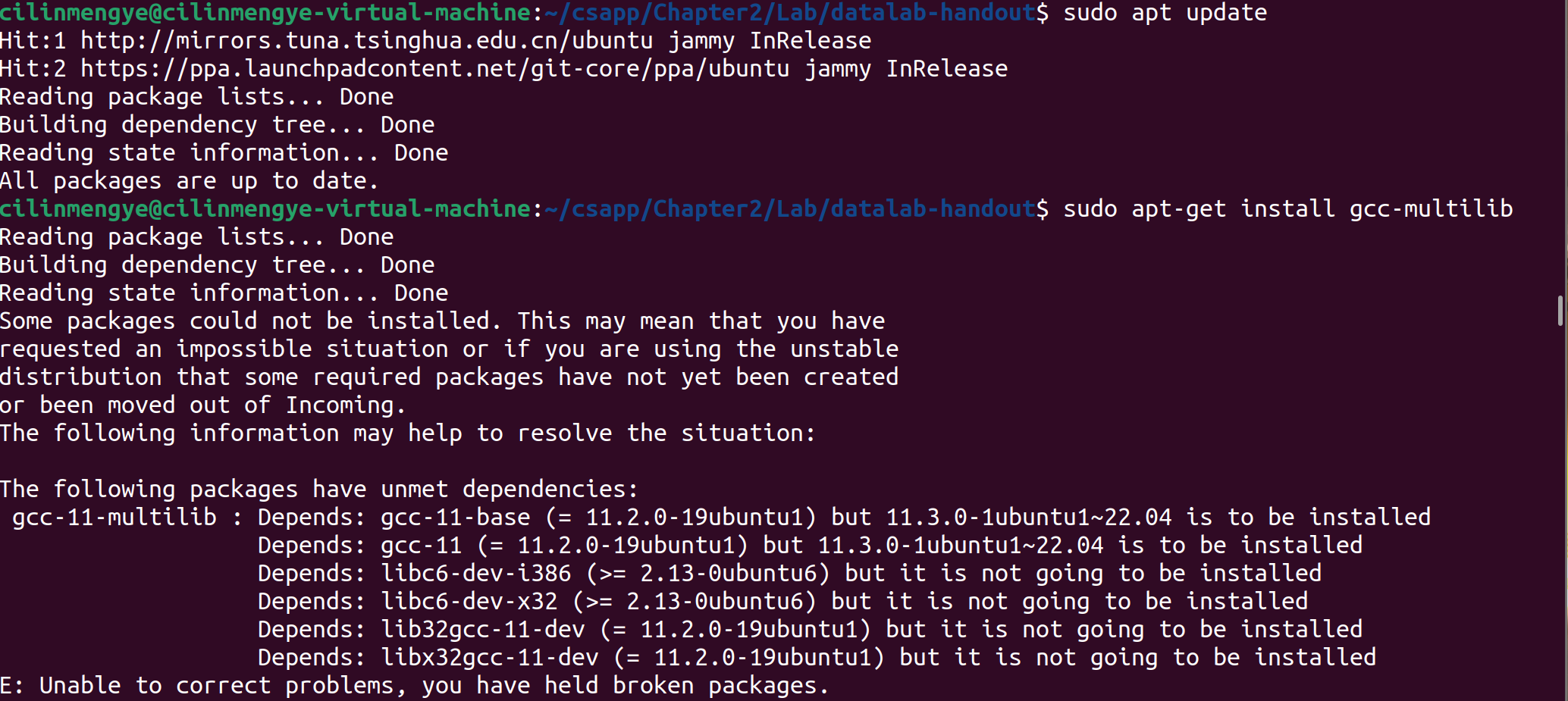
知识点

C中!与~的区别

非浮点数题目

个人感觉这些题目与"数字逻辑"中的"逻辑代数"非常像

(~x)+1 //可以得到-x,将只能用+的情况下，转变为可以用-

!(x^y) //可以用来代替==，==则为1，否则为0

逻辑函数表达式 可以用来代替 判断语句

如何理解 逻辑函数表达式 可以用来代替 判断语句？

• isLessOrEqual - if x <= y then return 1, else return 0
• Example: isLessOrEqual(4,5) = 1.
• Legal ops: ! ~ & ^ | + << >>

比如这道题目，我可以通过判断 sum=（~x）+1+y,sum是否为负数来判断是否 x<=y

但是这只适合x<0,y<0 或 x>0,y>0的情况

但是我还要注意下特殊情况：x<0,y>0 与 x>0,y<0; 这种情况下sum=（~x）+1+y，sum可能会溢出导致判断失误。

那么我的解题思路可以化为：

• x<0,y>0 return 1
• x>0,y<0 return 0
• x>0,y>0 或 x<0,y<0. sum>=0 return 1,sum<0 return 0

这看起来用if语句很好实现，但是我这里不能用，我应该如何办？

我们先拿出可以判断x,y,sum是否大（小）于0的“证据”吧。即他们的最高位：当最高位为1，小于0；反之大于等于0.

 int bx=(x>>31)&1;
 int by=(y>>31)&1;
 int sum=((~x)+1)+y;
 int bsum=sum>>31;

然后可以写出真值表出来：

bx	by	bsum	return
1	0	0	1
1	0	1	1
0	1	0	0
0	1	1	0
0	0	0	1
0	0	1	0
1	1	0	1
1	1	1	0

然后转换为逻辑函数，于是就可以用 逻辑运算符表示了

什么是真值表，如何转为逻辑函数？

return (bx&(~by)&(~bsum))|(bx&(~by)&bsum)|((~bx)&(~by)&(~bsum)))|(bx&by&(~bsum)))

浮点数题目

[CSAPP] 计算机如何表示浮点数

总之要理解清楚，IEEE754表示法，浮点数分为：

• 规格化exp!=0 && exp!=255
• 非规格化 exp==0
• infinity exp=0xFF && f==0
• NaN exp=0xFF && f!=0

floatScale2 - Return bit-level equivalent of expression 2*f for floating point argument f

这道题，需要分规格化与非规格化，规格化是在exp上+1，非规格化是在f上<<1

floatPower2 - Return bit-level equivalent of the expression 2.0^x

这道题，需要想清楚IEEE浮点数表示法中，最大能够表示多大的2^{x,以及最小能够表示的2}x

最小当然是非规格化时：
exp=0,E=1-127=-126
同时M=0.0000...0001

则最小表示为1*2^(-126-23)=1*2^(-149)

最大当然是规格化时：
exp=2^8-1-1=254（注意规格化的时候，exp!=255）
E=exp-127=127
同时M=1.1111...111

则最大表示为1.111...111*2^127

所以如果x<-149 || x>127 ，则分别是too small to be represented as a denorm, return 0; too large, return +INF.

同时要将2^x表示为IEEE浮点数，因为还有非规格化与规格化之分。所以我们还要知道非规格化最大表示和规格化最小表示

非规格化最大表示
exp=1-127=-126
M=0.1111...111

非规格化最大表示=1.111...111*2^(-127)

规格化最小表示
exp=1-127=-126（因为exp!=0在规格化下）
M=1.000...000

非规格化最大表示=1.000..000*2^(-126)

所以：

• x<-149 return 0
• x>127 return +INF
• -149<=x<=-127 表示为非规格化形态
• -126<=x<=127 表示为规格化形态

FIN

把感兴趣的作了，也算是基本上作完了吧，最后一题我个人感觉是没逻辑问题，看正确答案也是基本上也是这么做的，只是我的代码多了点判断（容易读）

github code