论文阅读 | Learning What and Where to Transfer

Learning What and Where to Transfer

概述

这是一篇来自 ICML 2019 的迁移学习论文。作者针对异构师生网络的知识迁移任务，提出了一种基于元学习的迁移学习方法，自动地学习源网络中什么知识需要迁移、迁移到目标网络的什么地方。也就是说，通过元学习来决定：
（a）源网络和目标网络之间的哪一对层应该匹配以进行知识迁移；
（b）哪些特征以及每个特征应该迁移多少知识。该方法在多个数据集以及网络结构上的表现明显优于其他算法。

介绍

深度学习需要大量的数据，但一些任务难以获得足够的数据。处理这种缺乏数据的一种有效方法是迁移学习，将知识从已知的源任务迁移到新的目标任务。比如首先在 ImageNet 上预训练，然后在目标任务的数据集上做微调就是一种迁移方法。但如果源任务和目标任务差异较大，那么微调就是没用的。
知识蒸馏则利用源网络（即教师网络）提供的知识（如软化输出、中间层特征、注意图等等）来辅助训练目标网络（即学生网络）。但以往的方法虽然允许异构师生网络之间迁移知识，但并没有机制来确定应该在师生网络的哪些层之间迁移哪些知识。有些源信息比另一些更重要，而且手工设置的源网络与目标网络的层匹配也未必是最优的。
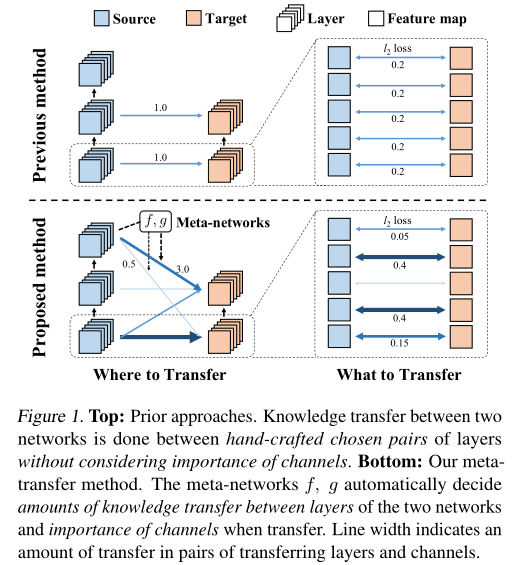
为了解决上述问题，作者提出了一种基于元学习的迁移学习方法，该方法学习需要迁移哪些知识以及这些知识应该迁移到目标网络的哪个层去。作者提出的方法与以往方法的对比如图 1 所示。具体来说，就是学习元网络以生成每个特征以及源网络和目标网络每对层之间的权重，这样就可以自动学习识别源网络的哪些知识是有用的，以及知识应该迁移到哪里。

方法

Learning What and Where to Transfer

作者使用元学习的策略来学习源网络的哪些知识要迁移到目标网络的哪个层。
（1）Weighted Feature Matching
显然，如果源网络是 well-trained 的，那么它中间层的特征空间包含对该任务的有用知识，对这些特征进行模仿可能有助于另一个网络的训练。记 \(x\)为输入，\(y\)为对应的 gt，我们假设源网络为 \(S\)，目标网络为 \(T_\theta\)，源网络第 \(m\)层的中间特征图为 \(S^m(x)\)，目标网络第 \(n\)层的中间特征图为 \(T_θ^n(x)\)。我们最小化特征图的 \(l_2\) 距离来实现知识迁移：

\[||r_{\theta}(T_{\theta}^n(x))-S^m(x)||_2^2 \]

其中 \(r_{\theta}\)是线性变换。对于一般的知识迁移任务，目标模型的任务和源模型的任务一般是不同的，在这种情况下并不是源模型的所有中间层特征都有益于目标任务的学习。于是作者对特征图的通道进行加权，得到加权特征匹配损失：

\[L^{m,n}_{wfm}(\theta|x,w^{m,n}) =\frac{1}{HW}\sum_c{w^{m,n}_c{\sum_{i,j}(r_\theta(T_\theta^n(x))_{c,i,j}-S^m(x)_{c,i,j})^2}} \]

考虑到对于每个输入图像来说，迁移通道的重要性对每个输入图像都不一样，所以这里 \(w_c^{m,n}\) 是一个函数：

\[w^{m,n}=[w_c^{m,n}]=f_\phi^{m,n}(S^m(x)) \]

meta 网络的输入为源模型的特征图，\(\phi\)为元网络的参数。
知识迁移不仅要考虑迁移哪些知识，还要考虑迁移到目标网络的哪一层。也就是说需要确定源模型和目标模型层之间的匹配，即 pair \((m,n)\)。以往的方法大多是根据对网络结构的先验知识或任务之间的语义相似性来手动设置的。怎样匹配源网络与目标网络的层更合理呢？作者为每对 \((m,n)\)引入了一个可学习参数 \(\lambda^{m,n}\ge0\)，并将其值设为元网络 \(g\)的输出：

\[L_{wfm}(\theta|x,\phi)=\sum_{(m,n)\in{C}}\lambda^{m,n}L^{m,n}_{wfm}(\theta|x,w^{m,n}) \]

其中 \(C\)是候选对。最终的损失为：

\[math L_{total}(\theta|x,\phi)=L_{org}(\theta|x,y)+{\beta}L_{wfm}(\theta|x,\phi) \]

其中 \(L_{org}\)是原始的损失（比如 CE），显然参数 \(w^{m,n}\)和 \(\lambda^{m,n}\)决定了迁移什么以及迁移到哪里。框架如图 2 所示：

Training Meta-Networks and Target Model

为了使性能最大化，特征匹配损失项 \(L_{wfm}(·|x,\phi)\)应该鼓励有助于目标任务的特征学习，比如预测标签。为了度量并提升由参数 \(\phi\)参数化的元网络决定的特征匹配的有用性，标准方法是使用以下双层策略来训练 \(\phi\):

更新 \(T\)次 \(\theta\)来最小化 \(L_{total}(\theta|x,y,\phi)\);
度量 \(L_{org}(\theta|x,y)\)并更新 \(\phi\)来最小化它。
可以发现，内循环实际采用的损失为 \(L_{total}(\theta|x,y,\phi)\)，而 \(L_{org}\)用于衡量学习到的目标模型的有效性。但由于这个方法中元网络是通过 \(L_{wfm}\)这个正则化项微弱地对目标模型的学习过程产生影响，所以除非使用大量的内循环迭代，不然使用梯度 \({\nabla}_{\phi}L_{org}\)来更新 \(\phi\)是很困难的。
于是，作者提出了一种交替更新的策略：
更新 \(T\)次 \(\theta\)来最小化 \(L_{wfm}(\theta|x,\phi)\);
更新一次\(\theta\)来最小化 \(L_{org}(\theta|x,y)\);
度量\(L_{org}(\theta|x,y)\)并更新 \(\phi\)来最小化它。
第一阶段，给定当前参数 \(\theta_0=\theta\)，通过最小化 \(L_{wfm}\)来更新目标模型 \(T\)次，这时网络参数为 \(\theta_T\)；第二阶段通过目标标签进行一步自适应，网络参数从 \(\theta_T\)更新为 \(\theta_{T+1}\)；第三阶段利用\(L_{org}(\theta_{T+1})\)来测量第一阶段和第二阶段使用的样本下目标模型适应目标任务的情况，然后通过更新元参数 \(\phi\)来最小化 \(L_{org}(\theta_{T+1})\)这样可以加速对 \(\phi\)的训练。文中的 \(T\)取 2。

作者通过使用 Hessian 向量积来有效地计算 \({\nabla}_{\phi}L_{org}(\theta_{T+1}|x,y)\)。

实验

作者在异构网络架构和任务上进行实验。
（1）使用 TinyImageNet 作为源任务，CIFAR-10、CIFAR-100 和 STL-10 作为目标任务，源任务使用 ResNet-32，目标任务使用 9 层的 VGG；
（2）使用 ImageNet 作为源任务，Caltech-UCSD Bird 200、MIT Indoor Scene Recognition、Stanford 40 Actions 和 Stanford Dogs 作为目标任务，源任务使用 ResNet-34，目标任务使用 ResNet-18。
在所有实验中，元网络的结构为：每对候选对 \((m,n)\in C\)为一层全连接网络。元网络以源网络第 m 层的 GAP 特征为输入，输出 \(w_c^{m,n}\)和 \(\lambda^{m,n}\)。通道加权参数 \(w\)使用 softmax 激活产生，满足 \(\sum_cw_c^{m,n}=1\)；层之间的迁移 \(\lambda\)则使用\(max(0,min(6,x))\)也就是 ReLU6，保证其非负性并避免值太大。几种层匹配策略对比如图 3 所示（这里以异构网络 ResNet32 和 VGG9 为例）：

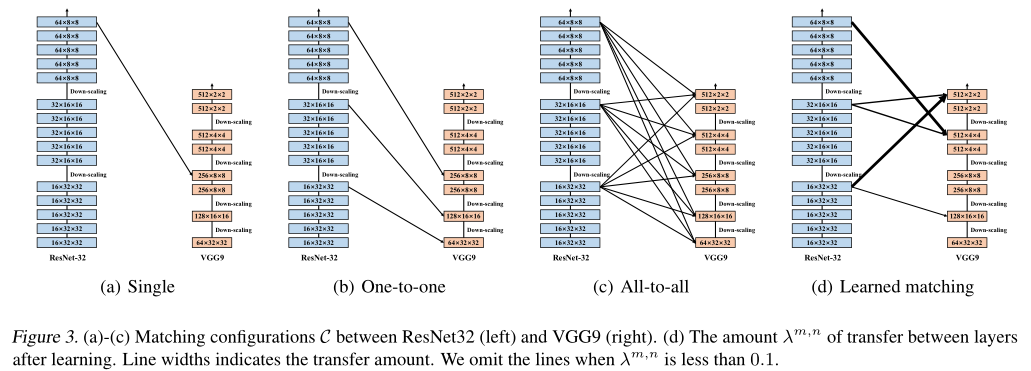
（a）single：使用源模型的最后一个特征层和目标模型中具有相同空间分辨率的层作为 pair；
（b）one-to-one：将每个下采样层前空间分辨率相同的层作为 pairs；
（c）all-to-all：使用每个下采样层前的所有 pairs。对于不同空间大小的特征匹配，使用双线性插值。
实验结果

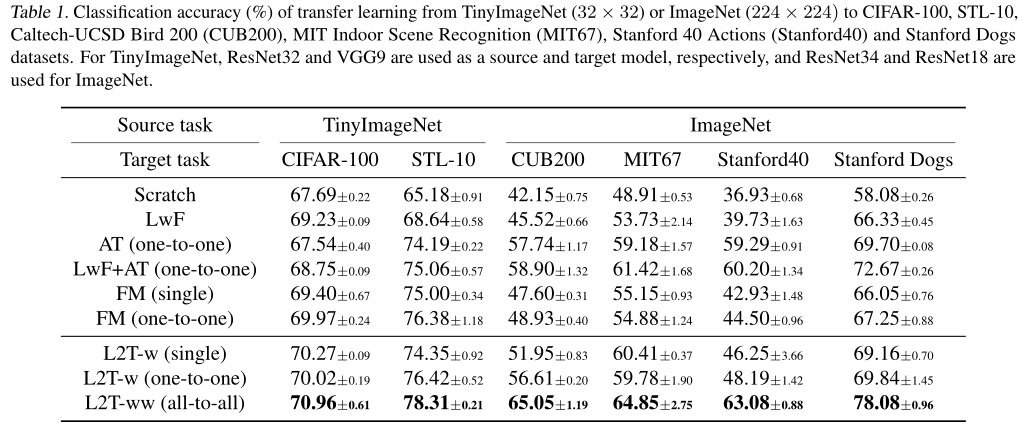
结果表明当目标任务具有特定类型的输入分布，而源模型为一般任务时，作者提出的方法更有效。而且，相比于只考虑迁移什么知识，同时考虑迁移什么知识及迁移到哪里的做法明显提升了网络性能，可以看到 L2T-ww 的性能大幅度优于其他方法。
然后，作者在有限样本的情况下进行实验：

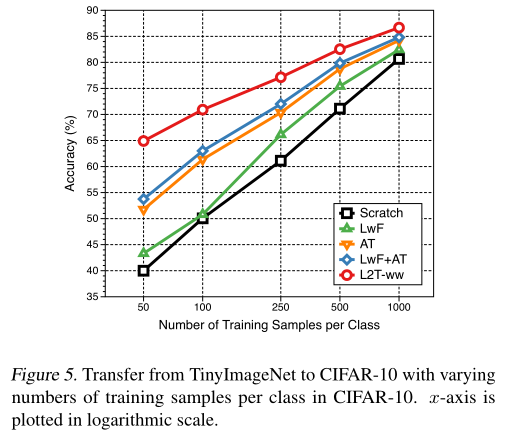
显然，在少量样本的情况下，L2T-ww 明显优于其他方法。
多源的知识迁移：

最后，作者对迁移什么知识进行了可视化分析，通过可视化知识迁移的注意力，对比未加权方法（FM）和加权方法（L2T-w）的 attention。可视化采用 saliency map：