LeetCode 9. 回文数

题目

题目链接：https://leetcode.cn/problems/palindrome-number/

给你一个整数x，如果x是一个回文整数，返回true；否则，返回false 。

回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

例如，121是回文，而123不是。

示例 1：

输入：x = 121
输出：true

示例 2：

输入：x = -121
输出：false
解释：从左向右读, 为-121。从右向左读, 为121-。因此它不是一个回文数。

示例 3：

输入：x = 10
输出：false
解释：从右向左读, 为01。因此它不是一个回文数。

解题

思路

映入脑海的第一个想法是将数字转换为字符串，并检查字符串是否为回文。但是，这需要额外的非常量空间来创建问题描述中所不允许的字符串。

第二个想法是将数字本身反转，然后将反转后的数字与原始数字进行比较，如果它们是相同的，那么这个数字就是回文。
但是，如果反转后的数字大于int.MAX，我们将遇到整数溢出问题。

按照第二个想法，为了避免数字反转可能导致的溢出问题，为什么不考虑只反转int数字的一半？毕竟，如果该数字是回文，其后半部分反转后应该与原始数字的前半部分相同。

例如，输入1221，我们可以将数字“1221”的后半部分从“21”反转为“12”，并将其与前半部分“12”进行比较，因为二者相同，我们得知数字1221是回文。

算法

首先，我们应该处理一些临界情况。所有负数都不可能是回文，例如：-123不是回文，因为 - 不等于3。所以我们可以对所有负数返回false。除了0以外，所有个位是0的数字不可能是回文，因为最高位不等于0。所以我们可以对所有大于0且个位是0的数字返回false。

现在，让我们来考虑如何反转后半部分的数字。

对于数字1221，如果执行1221 % 10，我们将得到最后一位数字1，要得到倒数第二位数字，我们可以先通过除以10把最后一位数字从1221中移除，1221 / 10 = 122，再求出上一步结果除以10的余数，122 % 10 = 2，就可以得到倒数第二位数字。如果我们把最后一位数字乘以10，再加上倒数第二位数字，1 * 10 + 2 = 12，就得到了我们想要的反转后的数字。如果继续这个过程，我们将得到更多位数的反转数字。

现在的问题是，我们如何知道反转数字的位数已经达到原始数字位数的一半？

由于整个过程我们不断将原始数字除以10，然后给反转后的数字乘上10，所以，当原始数字小于或等于反转后的数字时，就意味着我们已经处理了一半位数的数字了。

public boolean isPalindrome(int x) {
    String s = String.valueOf(x);
    int l = 0;
    int h = s.length() -1;
    while (l < h) {
        if (s.charAt(l) != s.charAt(h)) {
            return false;
        }
        l++;
        h--;
    }
    return true;
}    

官网题解

public boolean isPalindrome(int x) {
    // 特殊情况：
    // 如上所述，当x < 0时，x不是回文数。
    // 同样地，如果数字的最后一位是0，为了使该数字为回文，
    // 则其第一位数字也应该是0
    // 只有0满足这一属性
    if (x < 0 || (x % 10 == 0 && x != 0)) {
        return false;
  
    int revertedNumber = 0;
    while (x > revertedNumber) {
        revertedNumber = revertedNumber * 10 + x % 10;
        x /= 10;
  
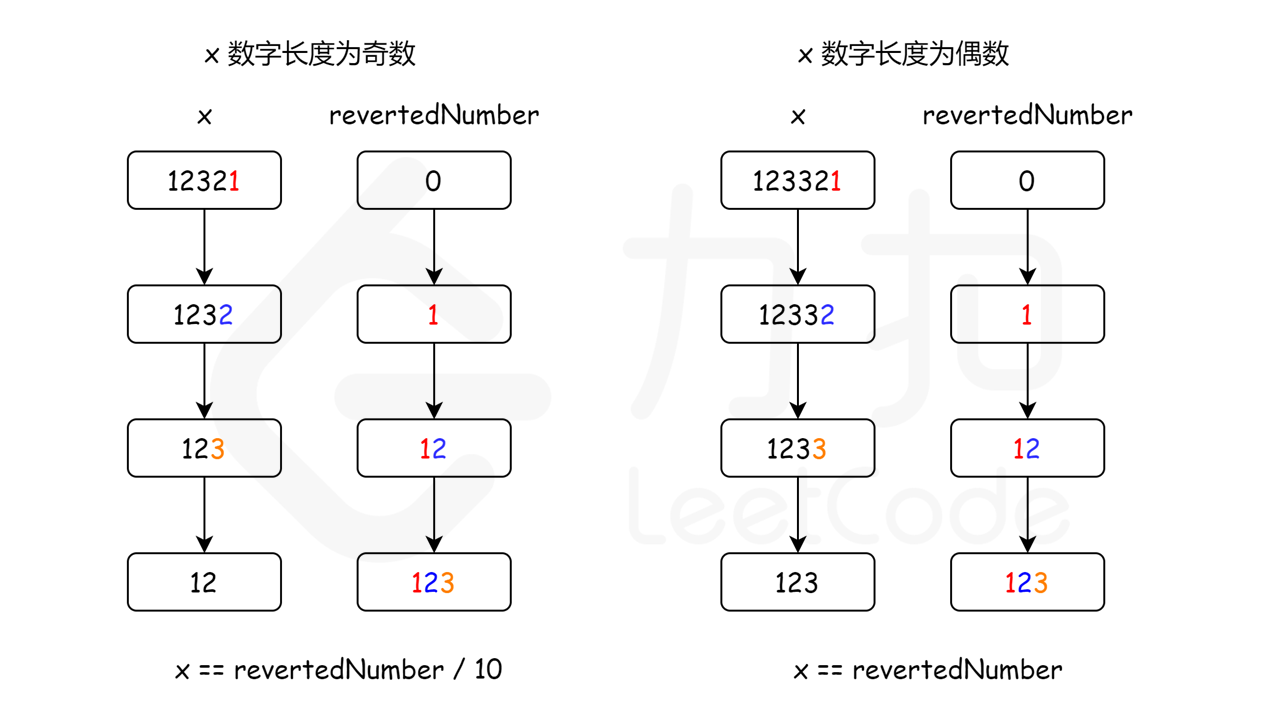
    // 当数字长度为奇数时，我们可以通过revertedNumber/10去除处于中位的数字。
    // 例如，当输入为12321时，在while循环的末尾我们可以得到 x = 12，revertedNumber = 123，
    // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
    return x == revertedNumber || x == revertedNumber / 10;
}