【算法】递归算法
一、基本原理和示例
在计算机程序中描述重复的一种方法是使用循环,如Java的while循环和for循环结构。实现重复的完全不同的方法是通过一个称为递归的过程。
递归是一种方法对自身进行一次或多次调用的技术,在执行期间,或数据结构依赖于同一类型的结构。有很多例子艺术与自然中的递归。例如,分形图案是自然递归的。艺术中使用递归的物理例子是俄罗斯的Matryoshka玩偶。每个玩偶要么是实木做的,要么是空心的,里面装着另一个奶嘴里面有洋娃娃。
在计算中,递归为执行重复性任务提供了一种优雅而强大的选择。实际上,一些编程语言(例如Scheme,Smalltalk)不显式支持循环构造,而是直接依赖关于表示重复的递归。大多数现代编程语言都支持函数递归,使用与支持传统形式的方法调用相同的机制。当调用,则该调用将挂起,直到递归调用完成。
递归是数据结构研究中的一项重要技术。我们从以下四个使用递归的示例开始,为每个示例提供了一个Java实现。
- 阶乘函数(通常表示为
n!)是一个经典的数学具有递归定义的自然函数。 - 英国尺子具有递归模式,这是分形的一个简单示例结构。
- 二进制搜索是最重要的计算机算法之一。它允许以高效地定位我们需要的数十亿个数据集条目的数量。
- 计算机的文件系统具有递归结构,其中目录可以任意深入嵌套在其他目录中。递归算法被广泛用于探索和管理这些文件系统。
1.1 递归示例
1.1.1 阶乘函数
为了演示递归机制,我们从一个简单的数学开始计算阶乘函数值的示例。正整数n的阶乘,用n表示!,定义为从1到n的整数的乘积。如果n=0,然后n!按惯例定义为1。更正式地说,对于任何n≥0的整数
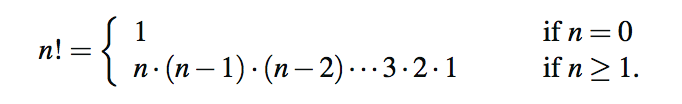
例如,5!=5·4·3·2·1=120。阶乘函数很重要,因为众所周知,它等于n个不同项目的排列方式变成一个序列,即n个项目的排列数。例如a、b、c三个字可以排成3! = 3 · 2 · 1 = 6ways:abc、acb、bac、bca、cab、cba。
阶乘函数有一个自然的递归定义。看到这个,注意5!=5·(4·3·2·1)=5·4!。更一般地说,对于正整数n,我们可以定义n!变成n·(n−1)!。这个递归定义可以形式化为

这个定义是许多函数递归定义中的典型定义。首先,我们有一个或多个基本情况,它们引用函数的固定值。以上定义有一个基本情况说明n!对于n=1。第二,我们有一个或者更递归的情况,根据函数本身定义函数。在上面定义中,有一个递归的例子,它表示n!=n·(n−1)!对于n≥1。
一个递归函数的实现
我们不能用递归的数学符号来设计factorial函数的实现:
public static int factorial(int n) throws IllegalArgumentException {
if (n < 0)
throw new IllegalArgumentException(); // argument must be nonnegative
else if (n == 0)
return 1; // base case
else
return n ∗ factorial(n - 1); // recursive case
}
此方法不使用任何显式循环。重复是通过方法的重复递归调用。这个过程是有限的,因为每个当方法被调用时,它的参数会变小一个,则不再进行递归调用。
我们演示了使用递归跟踪执行递归方法。每个跟踪项对应于递归调用。每次新的递归方法调用由指向新调用的向下箭头指示。当方法返回时,将绘制一个显示此返回值的箭头,并且返回值可以在该箭头旁边指示。阶乘函数的这种跟踪的示例如所示:
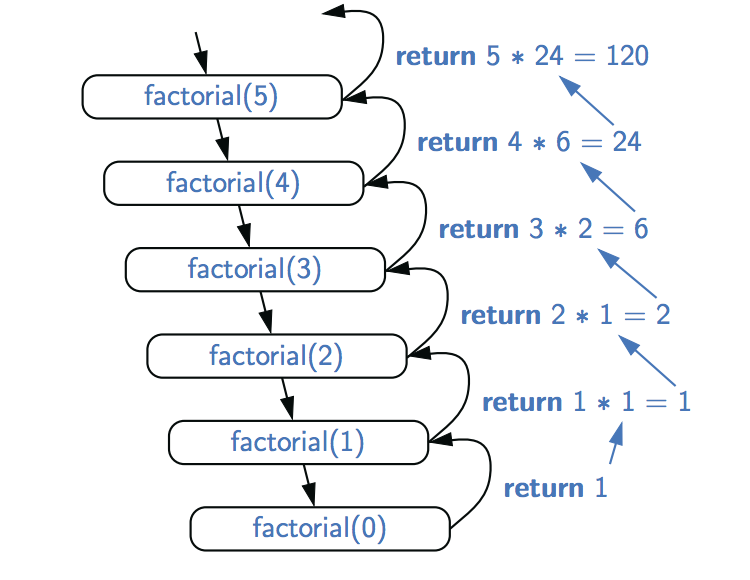
递归跟踪紧密地反映了编程语言对递归的执行。在Java中,每次调用一个方法(递归的或其他的)时,都会创建一个称为激活记录或激活帧的结构来存储有关该方法调用进度的信息。此框架存储特定于方法的给定调用的参数和局部变量,以及有关方法主体中当前正在执行的命令的信息。
当一个方法的执行导致一个嵌套方法调用时,前一个调用的执行被挂起,并且它的框架存储源代码中在返回嵌套调用时控制流应该继续的位置。然后为嵌套方法调用创建一个新的框架。此过程既可用于一个方法调用另一个方法的标准情况,也可用于方法调用自身的递归情况。关键点是每个活动呼叫都有一个单独的帧。
1.1.2 画英国尺子
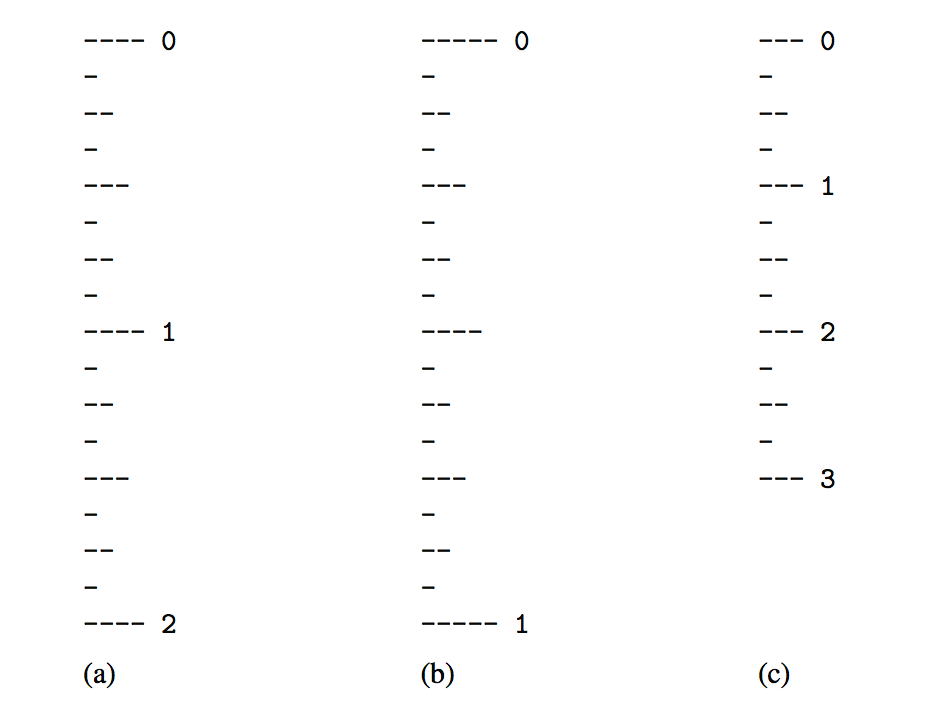
在计算阶乘函数的情况下,没有令人信服的理由比循环直接迭代更喜欢递归。作为使用递归的一个更复杂的例子,考虑一下如何绘制典型英国尺子的标记。对于每一英寸,我们都会用数字标签打勾。我们表示刻度的长度,表示整个英寸作为主要刻度长度。在表示整英寸的标记之间,标尺包含一系列小刻度,间隔为1/2英寸、1/4英寸,依此类推。当间隔的大小减少一半时,记号长度将减少1。图5.2展示了几种主要刻度长度不同的标尺(尽管没有按比例绘制)。
1.1.3 递归作图法
一个简单的,具有各种层次的分形结构。考虑图上图所示的主刻度长度为5的规则。忽略包含0和1的行,让我们考虑如何绘制位于这两行之间的记号序列。中央的滴答声(1/2英寸)的长度是4。请注意,这个中央记号上方和下方的两个记号图案是相同的,并且每一个都有一个长度为3的中央记号。
一般来说,中心刻度长度L≥1的间隔由以下组成:
- 中心刻度长度L−1的间隔
- 长度为L的单个刻度
- 中心刻度长度L−1的间隔
虽然可以使用迭代过程绘制这样一个标尺,但使用递归可以更容易地完成任务。我们的实现包括三个方法。
主要的方法,drawRuler,管理整个标尺的构造。它的参数指定标尺的总英寸数和主刻度长度。实用方法drawLine使用指定数量的短划线(以及打印在记号右侧的可选整数标签)绘制单个记号。
有趣的工作是用递归drawininterval方法完成的。此方法根据间隔中心刻度的长度绘制某个间隔内的次要刻度序列。我们依赖于本页顶部所示的直觉,以及当L=0时什么也不画的基本情况。对于L≥1,第一步和最后一步通过递归调用drawInterval(L−1)来执行。中间步骤通过调用方法drawLine(L)来执行。
/** Draws an English ruler for the given number of inches and major tick length. */
public static void drawRuler(int nInches, int majorLength) {
drawLine(majorLength, 0); // draw inch 0 line and label
for (int j = 1; j <= nInches; j++) {
drawInterval(majorLength − 1); // draw interior ticks for inch
drawLine(majorLength, j); // draw inch j line and label
}
}
private static void drawInterval(int centralLength) {
if (centralLength >= 1) { // otherwise, do nothing
drawInterval(centralLength − 1); // recursively draw top interval
drawLine(centralLength); // draw center tick line (without label)
drawInterval(centralLength − 1); // recursively draw bottom interval
}
}
private static void drawLine(int tickLength, int tickLabel) {
for (int j = 0; j < tickLength; j++)
System.out.print("-");
if (tickLabel >= 0)
System.out.print(" " + tickLabel);
System.out.print("\n");
}
/** Draws a line with the given tick length (but no label). */
private static void drawLine(int tickLength) {
drawLine(tickLength, −1);
}
二、递归的应用
2.1 用递归轨迹说明标尺绘图
递归drawInterval方法的执行可以使用递归跟踪可视化。然而,drawInterval的跟踪要比factorial示例复杂得多,因为每个实例都进行两次递归调用。为了说明这一点,我们将以一种类似于文档大纲的形式显示递归跟踪。见图:
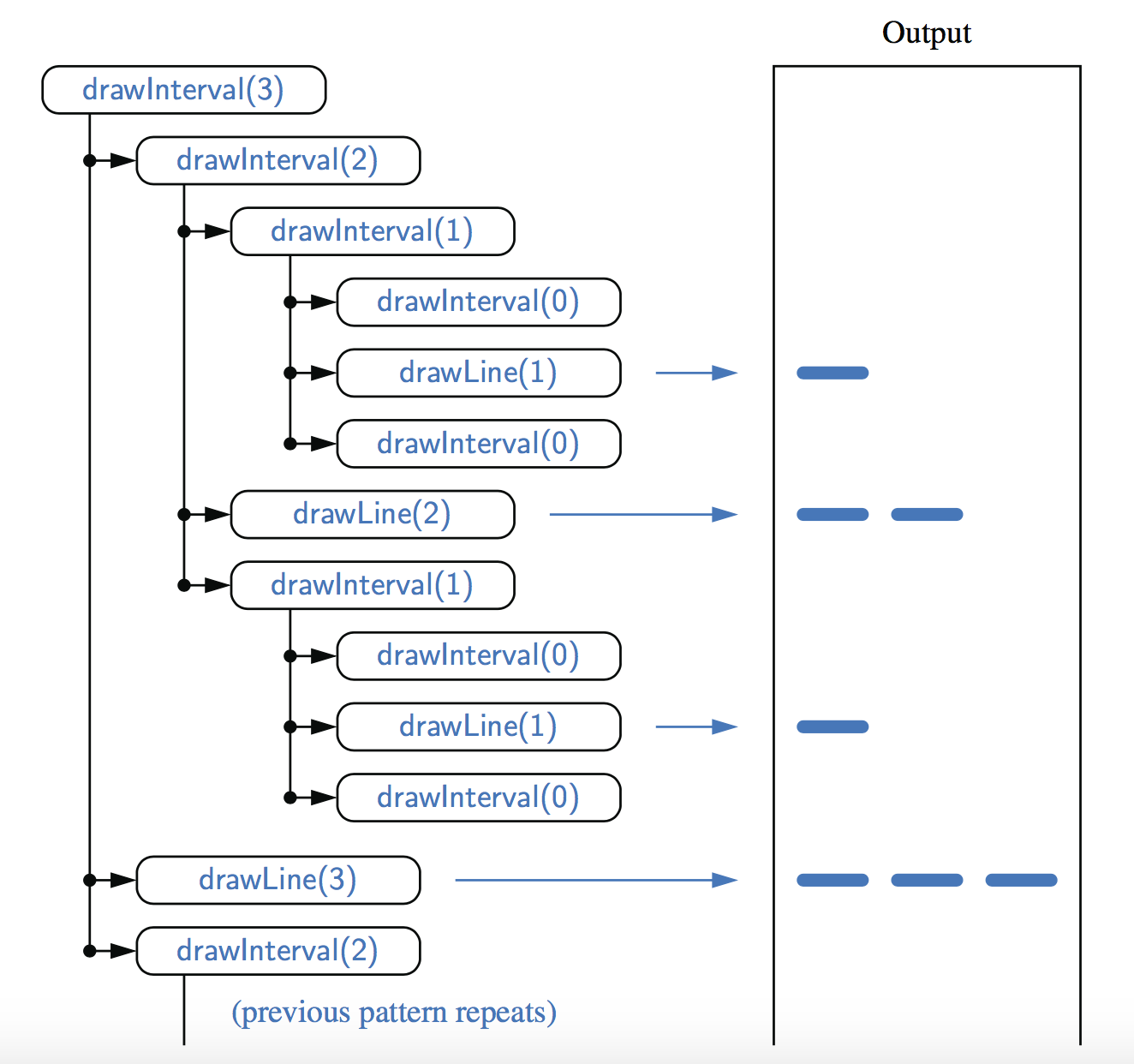
调用drawInterval(3)的部分递归跟踪。drawInterval(2)的第二种调用模式没有显示,但它与第一种模式相同。
2.2 二进制搜索
二进制搜索,用于在存储在数组中的n个元素的排序序列中有效地定位目标值。这是最重要的计算机算法之一,这也是我们经常按排序顺序存储数据的原因

数组中按排序顺序存储的值。最上面的数字是指数。
当序列未排序时,搜索目标值的标准方法是使用循环检查每个元素,直到找到目标或耗尽数据集为止。这种算法被称为线性搜索或顺序搜索,它在O(n)时间(即线性时间)内运行,因为每个元素都是在最坏的情况下检查的。
当序列是排序的和可索引的,有一个更有效的算法。(凭直觉,想想你如何用手完成这项任务!)如果我们考虑序列中任意一个元素的值为v,那么我们可以确定序列中该元素之前的所有元素的值都小于或等于v,并且序列中该元素之后的所有元素的值都大于或等于v。这个观察使我们能够使用一个变量快速“定位”搜索目标在儿童游戏“高低”中,如果在当前的搜索阶段,我们不能排除这个项目与目标匹配,我们就称序列中的一个元素为候选元素。该算法保持低和高两个参数,使所有候选元素的索引至少为低,最多为高。最初,低=0,高=n−1。然后我们将目标值与中间候选值进行比较,即,具有索引的元素:
mid = ⌊(low + high)/2⌋
我们考虑三种情况:
- 如果目标等于中间候选项,则我们找到了我们正在寻找的项目,搜索成功结束。
- 如果目标小于中间候选值,则我们在序列的前半部分重新出现,即从低到中-1的指数间隔。
- 如果目标大于中间候选值,则我们在序列的下半部分重复,即指数从mid+1到high的间隔。
如果低>高,则搜索失败,因为间隔[low,high]为空。
这种算法被称为二进制搜索。我们在代码片段中给出了一个Java实现,并在图中演示了算法的执行。顺序搜索在O(n)时间内运行,而更有效的二进制搜索在O(logn)时间内运行。这是一个显著的改进,如果n是10亿,logn只有30。
/**
* Returns true if the target value is found in the indicated portion of the data array.
* This search only considers the array portion from data[low] to data[high] inclusive.
*/
public static boolean binarySearch(int[ ] data, int target, int low, int high) {
if (low > high)
return false; // interval empty; no match
else {
int mid = (low + high) / 2;
if (target == data[mid])
return true; // found a match
else if (target < data[mid])
return binarySearch(data, target, low, mid − 1); // recur left of the middle
else
return binarySearch(data, target, mid + 1, high); // recur right of the middle
}
}
排序数组上二进制搜索算法的一种实现。
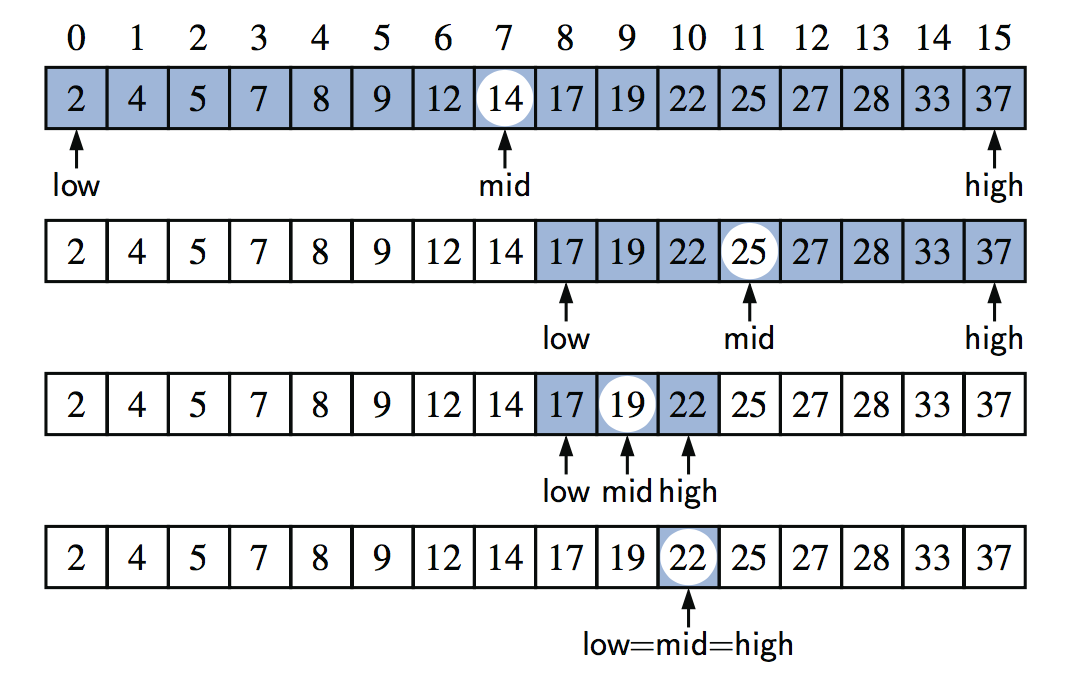
在包含16个元素的已排序数组上对目标值22进行二进制搜索的示例。
2.3 文件系统
现代操作系统以递归的方式定义文件系统目录(也称为“文件夹”)。也就是说,一个文件系统由一个顶级目录组成,这个目录的内容由文件和其他目录组成,这些目录又可以包含文件和其他目录,等等。操作系统允许对目录进行任意深度的嵌套(只要有足够的内存),尽管必须有一些只包含文件的基目录,而不包含其他子目录。下图给出了这种文件系统的一部分的表示。
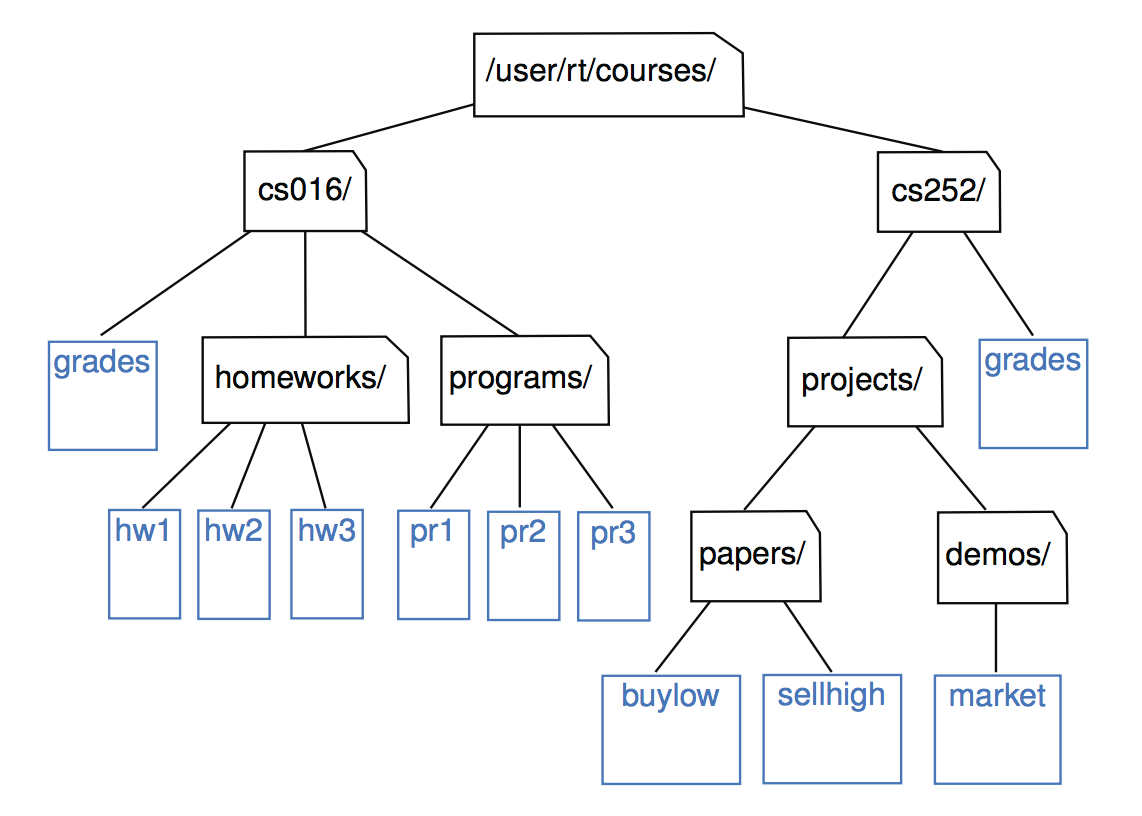
考虑到文件系统表示的递归性质,操作系统的许多常见行为(如复制目录或删除目录)都是用递归算法实现的,这一点也不奇怪。在本节中,我们考虑这样一种算法:计算嵌套在特定目录中的所有文件和目录的总磁盘使用量。
为了便于说明,下图描绘了示例文件系统中所有条目所使用的磁盘空间。我们区分每个条目使用的即时磁盘空间和该条目和所有嵌套功能部件使用的累积磁盘空间。例如,cs016目录只使用2K的立即空间,但总共使用249K的累积空间。
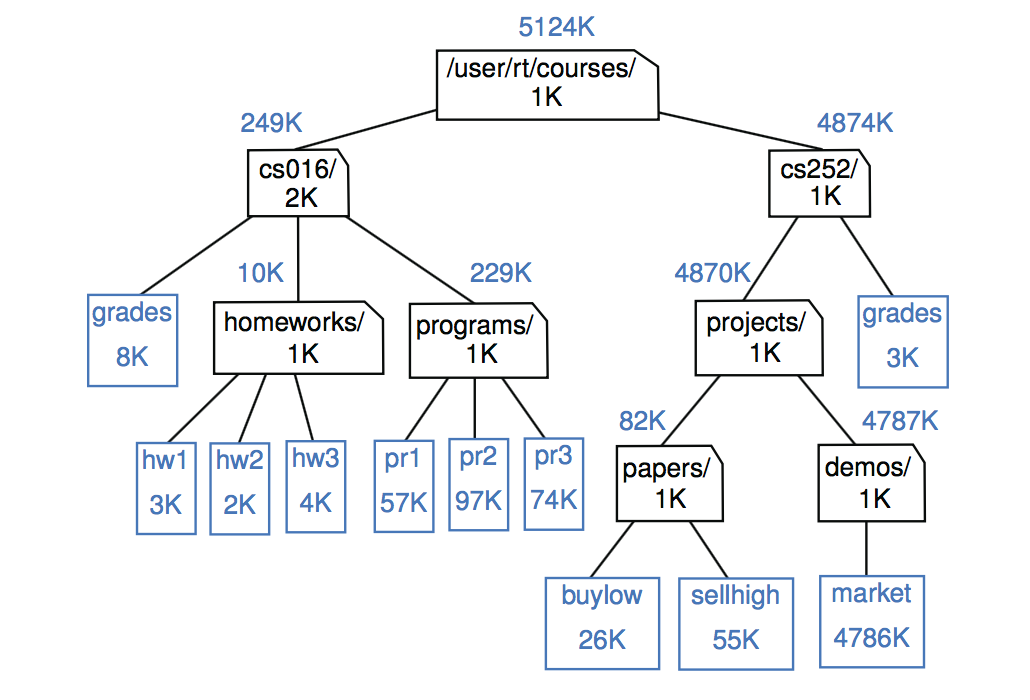
图中给出的文件系统的同一部分,但带有额外的注释来描述所使用的磁盘空间量。在每个文件或目录的图标中是该工件直接使用的空间量。每个目录的图标上方都指示了该目录及其所有(递归)内容所使用的累积磁盘空间。
一个条目的累积磁盘空间可以用一个简单的递归算法来计算。它等于条目使用的即时磁盘空间加上直接存储在条目中的任何条目的累计磁盘空间使用量之和。例如,cs016的累计磁盘空间是249K,因为它本身使用2K,等级累积使用8K,家庭作业中累积使用10K,程序中累积使用229K。
该算法的伪代码在代码片段如下:
Algorithm DiskUsage( path):
Input: A string designating a path to a file-system entry
Output: The cumulative disk space used by that entry and any nested entries
total = size( path) {immediate disk space used by the entry}
if path represents a directory then
for each child entry stored within directory path do
total = total + DiskUsage( child) {recursive call}
return total
一种计算嵌套在文件系统项上的累积磁盘空间使用量的算法。我们假设method size返回一个条目的即时磁盘空间。
2.4 Java.Io.File Class
为了在Java中实现计算磁盘使用量的递归算法,依赖于java.io.File。此类的实例表示操作系统中的抽象路径名,并允许查询该操作系统项的属性。我们将采用以下方法:
new File(pathString)或new File(parentFile,childString)通过提供一个新的目录项,或者提供一个新的目录项来指定一个新的目录项,或者在这个目录中提供一个新的目录项。file.length()返回由文件实例(例如,/user/rt/courses)表示的操作系统项的即时磁盘使用量(以字节为单位)。file.isDirectory()如果文件实例表示目录,则返回true;否则返回false。file.list()返回一个字符串数组,指定给定目录中所有项的名称。在我们的示例文件系统中,如果我们对与path/user/rt/courses/cs016关联的文件调用此方法,它将返回一个包含以下内容的数组:{“grades”、“homeworks”、“programs”}。
2.5 Java实现
通过使用File类,我们现在将算法从下面的代码片段实现。
/**
* Calculates the total disk usage (in bytes) of the portion of the file system rooted
* at the given path, while printing a summary akin to the standard 'du' Unix tool.
*/
public static long diskUsage(File root) {
long total = root.length( ); // start with direct disk usage
if (root.isDirectory( )) { // and if this is a directory,
for (String childname : root.list( )) { // then for each child
File child = new File(root, childname); // compose full path to child
total += diskUsage(child); // add child’s usage to total
}
}
System.out.println(total + "\t" + root); // descriptive output
return total; // return the grand total
}
磁盘文件递归报告系统的使用方法。
三、递归分析
3.1 递归跟踪
为了产生不同形式的递归跟踪,我们在Java实现中包含了一个无关的print语句。该输出的精确格式有意地镜像了一个名为du的经典Unix/Linux实用程序(用于“disk usage磁盘使用”)生成的输出。它报告一个目录所使用的磁盘空间量和嵌套在其中的所有内容,并可以生成一个详细的报告。
当在示例文件系统上执行时,我们对diskUsage方法的实现会产生下图给出的结果。在算法的执行过程中,对所考虑的文件系统部分中的每个条目只进行一次递归调用。因为每一行都是在递归调用返回之前打印的,所以输出行反映了递归调用完成的顺序。请注意,它先计算并报告嵌套项的累积磁盘空间,然后再计算和报告包含该项的目录的累积磁盘空间。例如,在计算包含它们的目录/user/rt/courses/cs016的累计总数之前,计算与条目成绩、家庭作业和程序有关的递归调用。

3.2 分析递归算法
使用递归算法,将根据在执行时管理控制流的方法的特定激活来说明执行的每个操作。换句话说,对于方法的每次调用,只考虑在激活主体中执行的操作的数量。然后,可以计算作为递归算法一部分执行的操作的总数量,方法是在所有激活中计算每次激活期间发生的操作数的总和。(顺便说一句,这也是分析一个非递归方法的方法,该方法从其主体中调用其他方法。)
为了证明这种分析方式,我们重新讨论了上节中提出的四种递归算法:阶乘计算 、绘制英语标尺 、二进制搜索 和文件系统累积大小的计算 。一般来说,可以依靠递归跟踪所提供的直觉来识别发生了多少次递归激活,以及如何使用每个激活的参数化来估计在该激活体中发生的原始操作的数量。然而,每种递归算法都有其独特的结构和形式。
3.2.1 计算阶乘
如上节所述,分析计算阶乘的方法的效率相对容易。为了计算阶乘(n),总共有n+1次激活,因为参数从第一次调用中的n减少到第二次调用中的n−1,依此类推,直到到达参数为0的基本情况。
通过对代码片段中的方法体的检查,还可以清楚地看到,factorial的每个单独激活都执行一个恒定数量的操作。因此,我们得出结论,计算阶乘(n)的操作总数是O(n),因为有n+1个激活,每个激活都占O(1)操作。
3.2.1 画英国尺子
在分析英制标尺应用程序时,我们考虑了一个有趣的问题,即最初调用drawInterval(c)生成了多少行输出,其中c表示中心长度。这是算法整体效率的一个合理的基准点,因为每一行输出都基于对drawLine实用程序的调用,而对drawInterval的每次递归调用都只对drawLine进行一次直接调用。
通过检查源代码和重现跟踪可以获得一些直觉。我们知道,对c>0的drawInterval(c)的调用会产生两个对drawInterval(c−1)的调用和对drawLine的单个调用。我们将依靠这个直觉来证明下面的说法。
命题:对于c≥0,调用drawInterval(c)将精确地生成2c−1行输出。
理由:我们通过归纳提供了这一索赔的正式证明。事实上,归纳法是证明递归过程正确性和效率的自然数学方法。对于标尺,我们注意到drawInterval(0)应用程序不会生成输出,而20−1=1−1=0。这是我们索赔的基本依据。
更一般地说,drawInterval(c)打印的行数是调用drawInterval(c−1)生成的行数的两倍多,因为两个递归调用之间打印一条中心线。通过归纳,我们得到线的数量因此为1+2·(2c−1−1)=1+2c−2=2c−1。
这一证明表明了一种更严格的数学工具,即递归方程,可用于分析递归算法的运行时间。在递归排序算法的上下文中讨论了该技术。
3.2.3 执行二进制搜索
考虑到在二进制搜索过程中每一次执行的二进制运算次数都为1.5。因此,运行时间与执行的递归调用的数量成正比。我们将证明,在对包含n个元素的序列进行二进制搜索时,最多会进行⌊logn⌋+1个递归调用,从而得到以下声明。
命题:对于有n个元素的排序数组,二进制搜索算法在O(logn)时间内运行。
理由:为了证明这一说法,一个关键的事实是,对于每个递归调用仍要搜索的候选元素的数量由该值给定
高-低+1。
此外,剩下的候选人人数至少减少了一半每个递归调用。具体来说,从mid的定义来看,剩余候选人的数量是
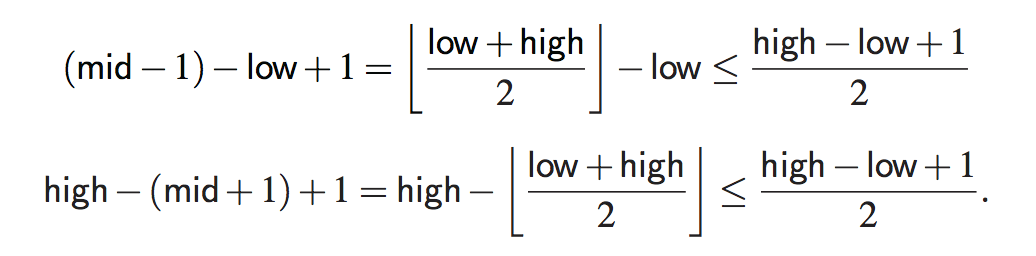
最初,候选数为n;在二进制搜索中,第一次调用后,最多为n/2;第二次调用后,最多为n/4;依此类推。一般来说,在二进制搜索的jth调用之后,剩余的候选元素的数目最多为n/2j。在最坏的情况下(搜索不成功),当不再有候选元素时,递归调用就会停止。因此,执行的最大递归调用数是最小的整数r,因此
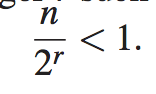
换句话说(回想一下,当对数的底是2时,我们省略了它),r是最小的整数,使得r>logn
r = log ⌋ + 1
这意味着二进制搜索在O(logn)时间内运行。
3.2.4 计算磁盘空间使用率
我们在上节中的最后一个递归算法是计算文件系统指定部分的总磁盘空间使用量。为了描述用于分析的“问题大小”,我们让n表示所考虑的文件系统部分中的文件系统条目数。
为了描述对diskUsage的初始调用所花费的累计时间,我们必须分析所进行的递归调用的总数,以及在这些调用中执行的操作数。
我们首先展示了该方法的精确n次递归调用,尤其是文件系统相关部分中的每个条目一次。直观地说,这是因为在处理包含e的唯一目录的条目时,仅在代码片段的for循环中对文件系统的特定条目e调用diskUsage,并且该条目只被探索一次。
为了形式化这个参数,我们可以定义每个条目的嵌套级别,使我们开始的条目具有嵌套级别0,直接存储在其中的条目具有嵌套级别1,存储在这些条目中的条目具有嵌套级别2,依此类推。我们可以通过归纳证明,在嵌套级别k的每个条目上,确实存在一次对diskUsage的递归调用。作为基本情况,当k=0时,唯一的递归调用是初始调用。作为归纳步骤,一旦我们知道在嵌套级别k的每个条目都有一次递归调用,我们就可以声明在嵌套级别k+1的每个条目e中只有一次调用,在包含e的k级条目的for循环中进行。
在确定文件系统的每个条目都有一个递归调用之后,我们回到算法的总计算时间问题上。如果我们可以争辩说我们在方法的任何一次调用中都花费了O(1)时间,那就太好了,但事实并非如此。在调用根部长度()若要直接在该条目处计算磁盘使用量,当该条目是一个目录时,diskUsage方法的主体包含一个for循环,该循环遍历该目录中包含的所有条目。在最坏的情况下,一个条目可能包含n−1个其他条目。
基于这个推理,我们可以得出结论:存在O(n)递归调用,每个调用都在O(n)时间内运行,导致总体运行时间为O(n2)。虽然这个上限在技术上是正确的,但它不是一个严格的上限。值得注意的是,我们可以证明递归算法在O(n)时间内完成的强界!较弱的界限是悲观的,因为它假定每个目录的条目数是最坏的情况。虽然有些目录可能包含与n成比例的多个条目,但它们不可能都包含那么多。为了证明更有力的说法,我们选择考虑for循环在所有递归调用中的总迭代次数。我们声称整个循环中确实有n-1次这样的迭代。我们基于这样一个事实,即该循环的每次迭代都对diskUsage进行递归调用,但我们已经得出结论:总共有n个对diskUsage的调用(包括原始调用)。因此,我们得出结论:存在O(n)个递归调用,每个调用都在循环之外使用O(1)时间,并且由于循环而导致的操作总数是O(n)。将所有这些界限相加,运算的总数是O(n)。
我们提出的论点比以前的递归例子更先进。我们有时可以通过考虑累积效应来获得一系列操作的更严格的限制,而不是假设每个操作都达到最坏的情况,这是一种称为摊销的技术;此外,文件系统是一种被称为树的数据结构的隐式示例,而我们的磁盘使用算法实际上是一种更通用的树遍历算法的体现。树将是第8章的重点,我们关于磁盘使用算法的O(n)运行时间的讨论将在第8.4节中推广到树遍历。
3.3 递归的进一步例子
在本节中,我们将提供递归用法的其他示例。我们通过考虑可能从单个激活体中启动的最大递归调用数来组织演示。
- 如果一个递归调用最多启动一个,我们称之为线性递归 。
- 如果一个递归调用可以启动另外两个调用,我们称之为二进制递归 。
- 如果一个递归调用可能启动三个或多个其他调用,则这是多个递归 。
3.3.1 线性递归
如果递归方法的设计使得对主体的每次调用最多进行一次新的递归调用,这就是所谓的线性递归 。在我们目前看到的递归中,阶乘方法的实现是线性递归的一个明显例子。更有趣的是,二进制搜索算法也是线性递归的一个例子,尽管名称中有“二进制”一词。二进制搜索的代码包括一个案例分析,有两个分支会导致进一步的递归调用,但是在主体的特定执行过程中,只跟随一个分支。
线性递归定义的一个结果是,任何递归跟踪都将显示为单个调用序列,注意,线性递归术语反映了递归跟踪的结构,而不是运行时间的渐近分析;例如,我们已经看到二进制搜索在O(logn)时间内运行。
3.3.2 递归求数组元素的总和
线性递归是处理序列(如Java数组)的有用工具。例如,假设我们要计算一个n个整数数组的和。我们可以使用线性递归来解决这个求和问题,方法是观察如果n=0,则总和通常为0,否则它是数组中的前n−1个整数加上数组中最后一个值的和。

通过将最后一个数加到第一个n−1的和上,递归地计算序列的和。
基于这种直觉计算整数数组和的递归算法在代码中实现。
/** Returns the sum of the first n integers of the given array. */
public static int linearSum(int[ ] data, int n) {
if (n == 0)
return 0;
else
return linearSum(data, n−1) + data[n−1];
}
下图给出了一个小例子的linearSum方法的递归轨迹。对于大小为n的输入,linearSum算法进行n+1方法调用。因为每次执行都会花费一部分时间。此外,我们还可以看到算法使用的内存空间(除了数组外)也是O(n),因为我们在进行最后一次递归调用(n=0)时,为跟踪中的n+1帧中的每个帧使用恒定数量的内存空间。

使用输入参数data=4、3、6、2、8执行linearSum(data,5)的递归跟踪。
四、递归实现
4.1 用递归反转序列
让我们考虑一个数组的n个元素的倒序问题,以便第一个元素成为最后一个元素,第二个元素成为倒数第二个元素,依此类推。我们可以使用线性递归来解决这个问题,通过观察序列的反转可以通过交换第一个和最后一个元素,然后递归地反转剩余的元素来实现。我们在代码中给出了该算法的一个实现,使用的约定是,我们第一次将此算法称为reverseArray(data,0,n−1)。
/** Reverses the contents of subarray data[low] through data[high] inclusive. */
public static void reverseArray(int[ ] data, int low, int high) {
if (low < high) { // if at least two elements in subarray
int temp = data[low]; // swap data[low] and data[high]
data[low] = data[high];
data[high] = temp;
reverseArray(data, low + 1, high − 1); // recur on the rest
}
}
我们注意到,每当进行递归调用时,数组相关部分中的元素将减少两个。当条件low<high失败时,最终达到一个基本情况,原因是n为奇数时low==high,或n为偶数时low==high+1。
上面的参数意味着代码中的递归算法保证在总共1+n次递归调用之后终止。每次打电话都是因为如果子阵列中至少有两个元素交换数据[low]和data[high],涉及一个恒定的工作量,整个过程在O(n)时间内运行。
4.2 计算幂的递归算法
作为使用线性递归的另一个有趣的例子,我们考虑将一个数x提升为任意非负整数n的问题。也就是说,我们希望计算幂函数,定义为幂(x,n)=xn。(我们在讨论中使用“power”这个名称,以区别于Math类的pow方法,后者提供了这样的功能。)我们将考虑两种不同的递归公式来解决导致算法性能截然不同的问题。
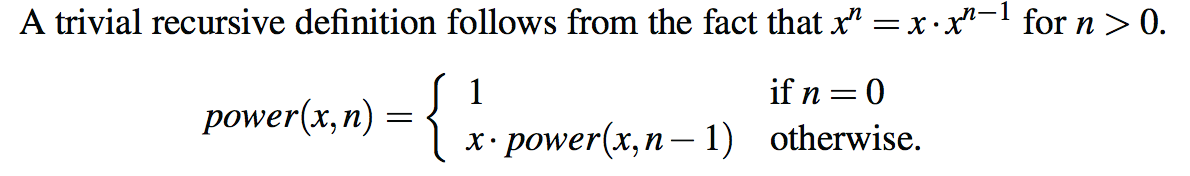
/** Computes the value of x raised to the nth power, for nonnegative integer n. */
public static double power(double x, int n) {
if (n == 0)
return 1;
else
return x ∗ power(x, n−1);
}
对这个power(x,n)版本的递归调用在O(n)时间内运行。它的递归跟踪结构与图中的阶乘函数的结构非常相似,每次调用时参数都会减少一个,并且在n+1级别的每个级别上都执行恒定的工作。
然而,有一种更快速的方法来计算幂函数,使用另一种定义,即使用平方技术。设k=n表示整数除法的底数(当n是int时,相当于Java中的n/2)。我们考虑如下方式:
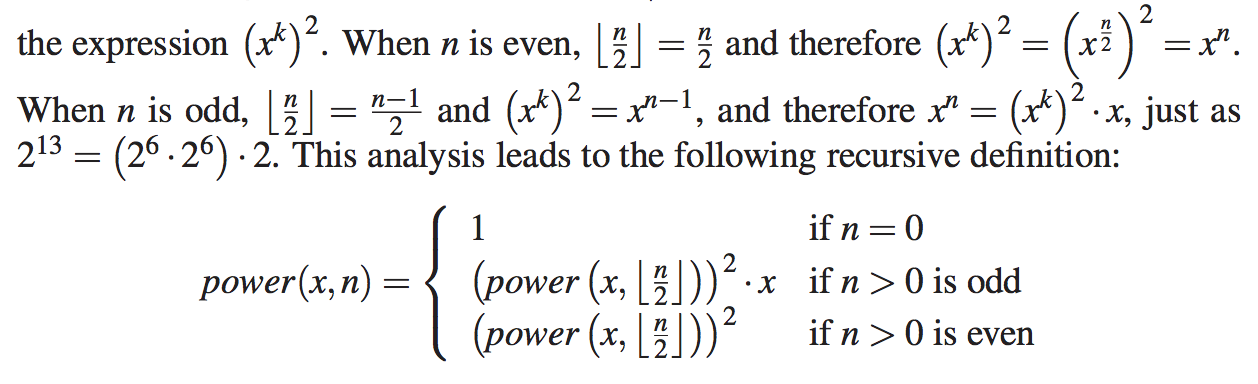
/** Computes the value of x raised to the nth power, for nonnegative integer n. */
public static double power(double x, int n) {
if (n == 0)
return 1;
else {
double partial = power(x, n/2); // rely on truncated division of n
double result = partial ∗ partial;
if (n % 2 == 1) // if n odd, include extra factor of x
result ∗= x;
return result;
}
}
为了说明改进算法的执行,图中提供了一个计算能力的递归跟踪power(2, 13)。
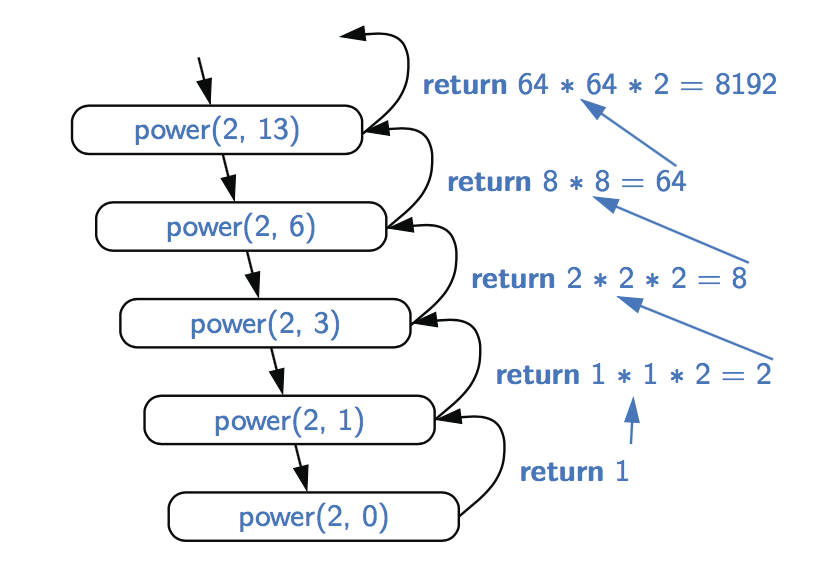
为了分析修正算法的运行时间,我们观察到每次方法幂(x,n)的递归调用中的元素最多为前一个指数的一半。正如我们在二进制搜索的分析中看到的,在得到1或更少之前,我们可以将n除以2的次数是O(logn)。因此,我们新的幂函数公式会导致O(logn)递归调用。方法的每个单独激活都使用O(1)操作(不包括递归调用),因此计算power(x,n)的操作总数为O(logn)。这是对原O(n)时间算法的一个显著改进。
改进后的版本在减少内存使用方面也提供了显著的节省。第一个版本的递归深度为O(n),因此O(n)帧同时存储在内存中。因为改进版本的递归深度是O(logn),所以它的内存使用量也是O(logn)。
4.3 二进制递归
当一个方法进行两次递归调用时,我们说它使用二进制递归。我们已经看到了绘制英制标尺时二进制递归的例子。作为二进制递归的另一个应用,让我们重新讨论一下数组的n个整数求和的问题。计算一个或零值之和是微不足道的。对于两个或两个以上的值,我们可以递归地计算前半部分的和和和后一半的和,并将这些和相加。在代码中,我们对这种算法的实现最初被调用为binarySum(data,0,n−1)。
/** Returns the sum of subarray data[low] through data[high] inclusive. */
public static int binarySum(int[ ] data, int low, int high) {
if (low > high) // zero elements in subarray
return 0;
else if (low == high) // one element in subarray
return data[low];
else {
int mid = (low + high) / 2;
return binarySum(data, low, mid) + binarySum(data, mid+1, high);
}
}
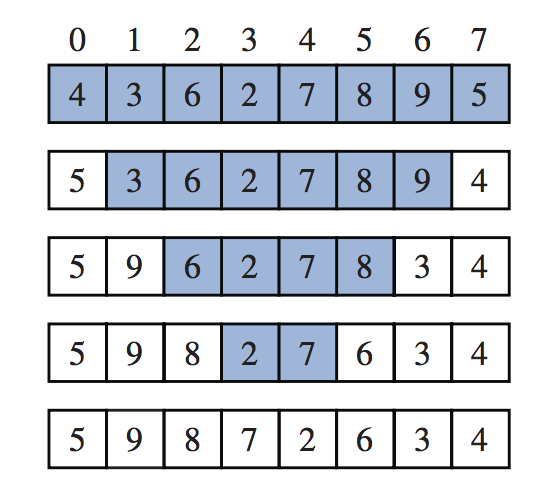
为了分析二进制求和算法,为了简单起见,我们考虑了n是2的幂的情况。图5.13显示了binarySum(data,0,7)执行的递归跟踪。我们用该调用的参数值low和high标记每个框。在每次递归调用时,范围的大小被一分为二,因此递归的深度是1+log2n。因此,binarySum使用O(logn)的额外空间,这比代码中linearSum方法使用的O(n)空间有很大的改进。但是,binarySum的运行时间是O(n),因为有2n−1个方法调用,每个调用都需要固定的时间。
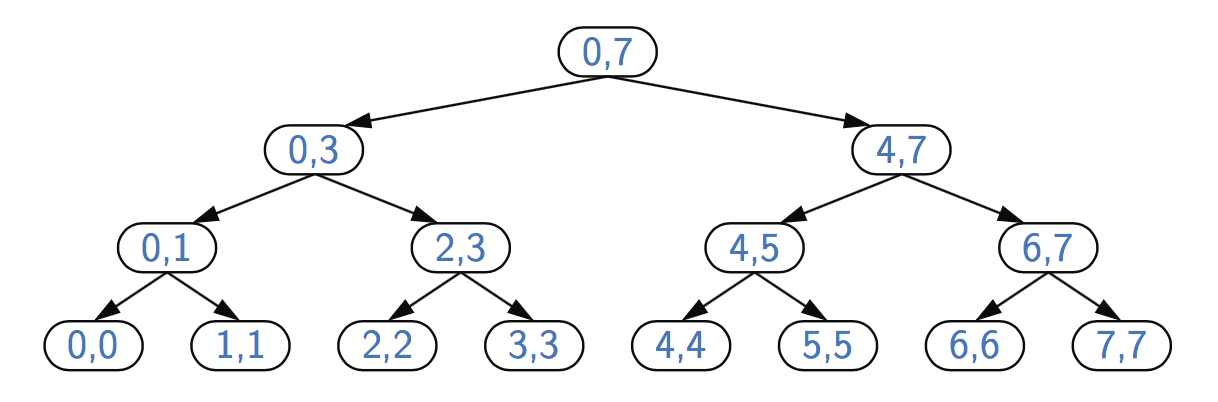
4.4 多重递归
从二进制递归中推广,我们将多重递归定义为一个过程,其中一个方法可以进行两个以上的递归调用。我们分析文件系统磁盘空间使用情况的递归是多重递归 的一个例子,因为在一次调用期间进行的递归调用的数量等于文件系统给定目录中的条目数。
多重递归的另一个常见应用是当我们想要枚举各种配置以解决组合难题时。例如,以下是所有被称为求和谜题的实例:
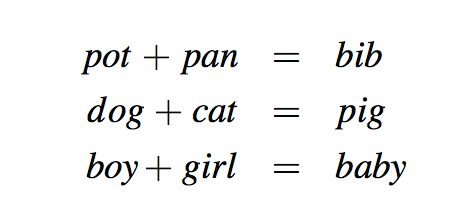
为了解决这个难题,我们需要给等式中的每个字母指定一个唯一的数字(即0,1,…,9),以使方程成立。通常,我们通过对我们试图解决的特定难题的人类观察来解决这样一个难题,以消除配置(即,可能的数字到字母的部分分配),直到我们能够处理剩余的可行配置,测试每个配置的正确性。
然而,如果可能配置的数量不是太多,我们可以使用计算机简单地列举所有的可能性并测试每一种可能性,而不需要人工观察。这种算法可以使用多重递归来系统地处理配置。为了保持描述的通用性,以便与其他谜题一起使用,我们考虑了一种算法,该算法从给定的宇宙U中选择并测试所有k长度的序列,无需重复。我们在代码中展示了这种算法的伪代码,通过以下步骤构建k个元素的序列:
- 递归生成k−1元素序列
- 在每个这样的序列中附加一个尚未包含在其中的元素
在整个算法的执行过程中,我们使用一个集合U来跟踪当前序列中没有包含的元素,因此当且仅当e是inU时,元素e还没有被使用。
另一种看待代码片段算法的方法是,它枚举U的每一个可能的大小为k的有序子集,并测试每个子集是否是我们难题的可能解决方案。
对于求和谜题,U={0,1,2,3,4,5,6,7,8,9}并且序列中的每个位置对应于一个给定的字母。例如,第一个位置可以代表b,第二个代表o,第三个代表y,依此类推。
Algorithm PuzzleSolve(k, S, U):
Input: An integer k, sequence S, and set U
Output: An enumeration of all k-length extensions to S using elements in U
without repetitions
for each e in U do
Add e to the end of S
Remove e from U {e is now being used}
if k = = 1 then
Test whether S is a configuration that solves the puzzle
if S solves the puzzle then
add S to output {a solution}
else
PuzzleSolve(k−1, S, U) {a recursive call}
Remove e from the end of S
Add e back to U
在图中,我们展示了对PuzzleSolve(3,S,U)调用的递归跟踪,其中S为空,U={a,b,c}。在执行过程中,生成并测试三个字符的所有排列。最初的三个调用依次进行两个递归调用。如果我们在一个由四个元素组成的集合U上执行PuzzleSolve(3,S,U),初始调用将进行四次递归调用,每个调用都有一个如图所示的轨迹。
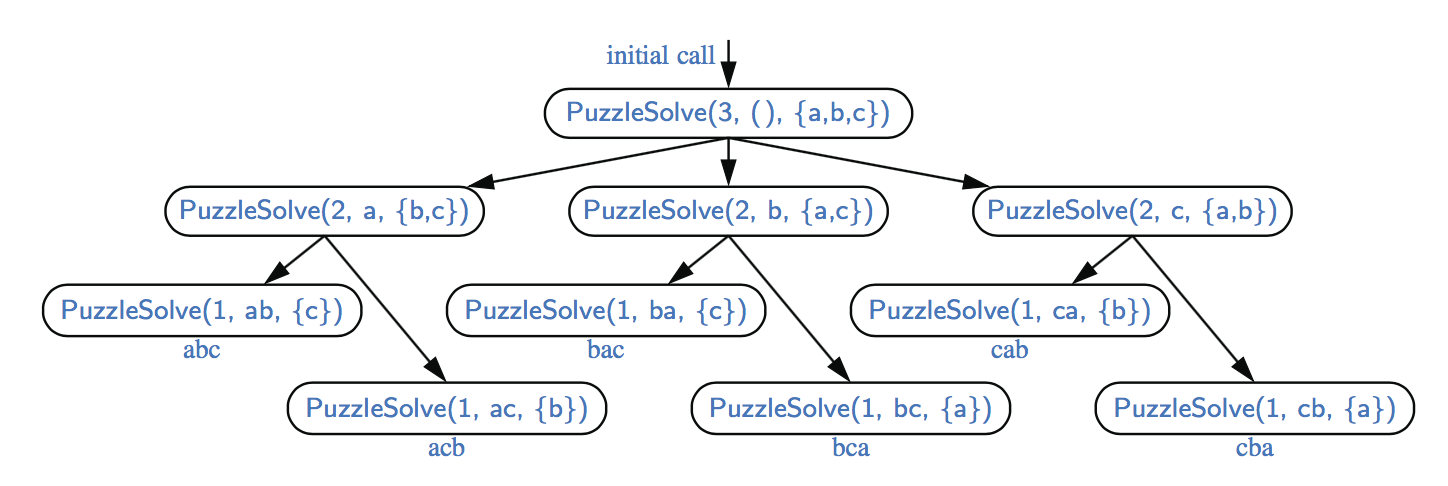
执行PuzzleSolve(3,S,U)的递归跟踪,其中S为空,U={a,b,c}。此执行生成并测试a、b和c的所有置换。我们将在它们各自的框的正下方显示生成的置换。
使用递归的算法通常具有以下形式:
- 基本情况测试。我们首先测试一组基本情况(至少应该有一个)。应该定义这些基本用例,以便每个可能的递归调用链最终都会到达一个基本用例,并且每个基本用例的处理不应该使用递归。
- 复发。如果不是基本情况,则执行一个或多个递归调用。此重复步骤可能涉及一个测试,该测试决定要进行几个可能的递归调用中的哪一个。我们应该定义每个可能的递归调用,以便它朝着一个基本情况前进。
4.5 参数化递归
为了设计一个给定问题的递归算法,我们可以考虑不同的方法来定义与原始问题具有相同总体结构的子问题。如果一个人很难找到设计递归算法所需的重复结构,那么有时可以通过几个具体的例子来解决问题,看看如何定义子问题。
成功的递归设计有时需要我们重新定义原始问题,以便于类似的子问题。通常,这涉及重新参数化方法的签名。例如,在数组中执行双线性搜索时,调用者的自然方法签名将显示为binarySearch(data,target)。然而,我们定义了我们的方法,调用签名二进制搜索(data,target,low,high),在递归过程中使用附加参数来划分子数组。参数化的这种变化对于二进制搜索是至关重要的。本章中的其他几个示例(例如reverseArray、linearSum、binarySum)也演示了在定义递归子问题时使用附加参数。
如果我们希望为算法提供一个更干净的公共接口,而不向用户公开递归参数化,标准技术是使递归版本私有化,并引入一个更干净的公共方法(用适当的参数调用私有方法)。例如,我们可以提供以下更简单的binarySearch版本供公众使用:
/** Returns true if the target value is found in the data array. */
public static boolean binarySearch(int[ ] data, int target) {
return binarySearch(data, target, 0, data.length − 1); // use parameterized version
}
五、递归的优缺点
5.1 递归的缺点和问题
虽然递归是一种非常强大的工具,但它很容易被以各种方式滥用。我们可以使用下面的递归公式来确定序列的n个元素是否都是唯一的。作为基本情况,当n=1时,元素通常是唯一的。对于n≥2,当且仅当前n−1个元素是唯一的,最后n−1个元素是唯一的,并且第一个和最后一个元素是不同的(因为这是唯一一个没有被检查为子类的对)。基于此思想的递归实现在代码片段中给出,名为unique3(以区别于上一章中的unique1和unique2)。
/** Returns true if there are no duplicate values from data[low] through data[high].*/
public static boolean unique3(int[ ] data, int low, int high) {
if (low >= high)
return true; // at most one item
else if (!unique3(data, low, high−1))
return false; // duplicate in first n−1
else if (!unique3(data, low+1, high))
return false; // duplicate in last n−1
else
return (data[low] != data[high]); // do first and last differ?
}
不幸的是,这是一个非常低效的递归使用。每个调用的非递归部分使用O(1)时间,因此总的运行时间将与递归调用的总数成比例。为了分析这个问题,我们让n表示考虑中的条目数,也就是说,让n=1+high-low。
如果n=1,那么unique3的运行时间是O(1),因为这种情况下没有递归调用。在一般情况下,重要的观察是,对大小为n的问题的unique3的单个调用可能导致对大小为n−1的问题进行两次递归调用。这两个大小为n−1的调用反过来可能会导致四个大小为n−2的调用(每个调用两个),从而导致8个大小为n−3的调用,依此类推。因此,在最坏的情况下,方法调用的总数由几何求和给出
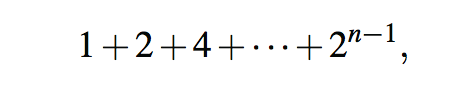
根据命题等于2n−1。因此,方法unique3的运行时间是O(2n)。对于解决元素唯一性问题来说,这是一种极其低效的方法。它的低效并不是因为它使用递归,而是因为它使用递归很差。
5.1.1 计算Fibonacci数的一种低效递归算法
我们介绍了一个生成Fi-bonacci数级数的过程,该过程可递归定义如下:
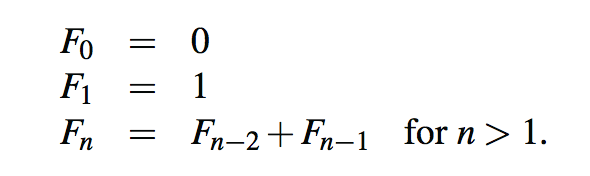
讽刺的是,直接基于这个定义的递归实现会产生代码片段中所示的fibonacciBad方法,该方法通过在每个非基本情况下进行两次递归调用来计算一个Fibonacci数。
/** Returns the nth Fibonacci number (inefficiently). */
public static long fibonacciBad(int n) {
if (n <= 1)
return n;
else
return fibonacciBad(n−2) + fibonacciBad(n−1);
}
不幸的是,这种直接实现Fibonacci公式的结果是一个非常低效的方法。以这种方式计算第n个Fibonacci数需要对方法进行指数级调用。具体地说,让cn表示在执行fibonacciBad(n)时执行的调用数。然后,我们得到cn的以下值:
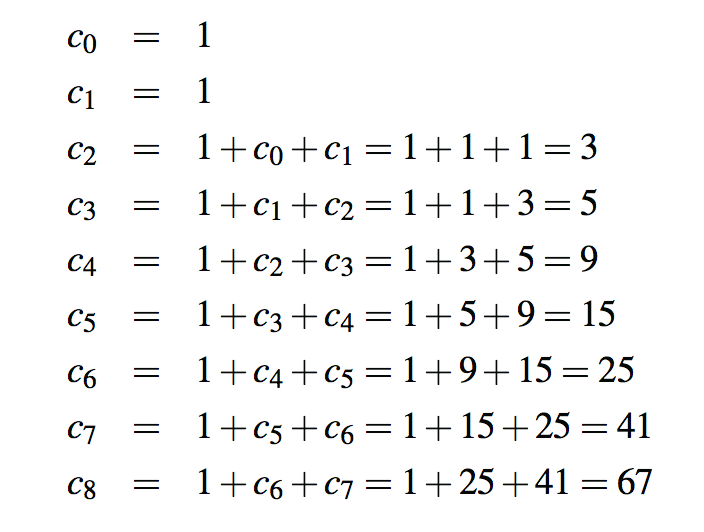
如果我们按照这个模式前进,我们会发现,每两个连续的索引,调用的数量都会增加一倍以上。也就是说,c4是c2的两倍以上,c5是c3的两倍以上,c6是c4的两倍以上,依此类推。因此,cn>2n/2,这意味着fibonacciBad(n)发出的调用数在n中是指数级的。
5.1.2 计算Fibonacci数的一种有效递归方法
因为第n个Fibonacci数Fn依赖于前面两个值Fn−2和Fn−1,我们被诱惑使用了糟糕的递归公式。但是请注意,在计算Fn−2之后,对compute Fn−1的调用需要自己的递归调用来计算Fn−2,因为它不知道在早期递归级别计算的Fn−2的值。那是重复劳动。更糟糕的是,这两个调用都需要(重新)计算Fn−3的值,以及Fn−1的计算。正是这种滚雪球效应导致了腓肠肌的指数运行时间。
我们可以更有效地使用递归计算Fn,其中每个调用只进行一个递归调用。为此,我们需要重新定义方法的经验。我们没有让方法返回一个值,即第n个Fibonacci数,而是定义了一个递归方法,该方法使用F−1=0的约定,返回具有两个连续Fibonacci数{Fn,Fn−1}的数组。虽然报告两个连续的Fibonacci数而不是一个似乎是一个更大的负担,但是将这些额外的信息从一个递归级别传递到下一个级别,使得继续该过程更加容易。(它允许我们避免重新计算递归中已知的第二个值。)基于此策略的实现在代码片段5.14中给出。
/**
* Returns array containing the pair of Fibonacci numbers, F(n) and F(n−1).
*/
public static long[ ] fibonacciGood(int n) {
if (n <= 1) {
long[ ] answer = {n, 0};
return answer;
} else {
long[ ] temp = fibonacciGood(n − 1); // returns {Fn−1, Fn−2}
long[ ] answer = {temp[0] + temp[1], temp[0]}; // we want {Fn, Fn−1}
return answer;
}
}
就效率而言,对于这个问题,坏的和好的递归之间的区别就像白天和黑夜一样。fibonacciBad方法使用指数时间。我们声称fibonacciGood(n)方法的执行在O(n)时间内运行。每次对fibonacciGood的递归调用都会将参数n减少1;因此,递归跟踪包括一系列n个方法调用。因为每个调用的非递归工作使用恒定时间,所以整个计算在O(n)时间内执行
5.1.3 Java中的最大递归深度
滥用递归的另一个危险是无限递归 。如果每个递归调用都执行另一个递归调用,而没有达到基本情况,那么我们就有一个无限系列的此类调用。这是一个致命的错误。无限递归可以迅速地淹没计算资源,这不仅是由于CPU的快速使用,而且因为每个连续的调用都会创建一个需要额外内存的帧。下面是格式错误的递归的一个明显例子:
/** Don't call this (infinite) version. */
public static int fibonacci(int n) {
return fibonacci(n); // After all Fn does equal Fn
}
然而,还有更细微的错误会导致无限递归。重温我们的二进制搜索实现,当我们对序列的右侧部分进行递归调用时,我们指定从索引mid+1到high的子数组。那句话是不是改成了
return binarySearch(data, target, mid, high); // sending mid, not mid+1
这可能导致无限递归 。特别是,当搜索两个元素的范围时,可以对相同的范围进行递归调用。
程序员应该确保每个递归调用都在某种程度上朝着一个基本情况前进(例如,通过使参数值随每次调用而减少)。为了对抗无限递归,Java的设计者有意地决定限制用于存储同时活动方法调用的激活帧的总空间。如果达到此限制,Java虚拟机将抛出StackOverflowError 。此限制的精确值取决于Java安装,但一个典型值可能允许1000个以上的同时调用。
对于许多递归应用程序,允许多达1000个嵌套调用就足够了。例如,我们的二进制搜索方法具有O(logn)递归深度,因此要达到默认的递归限制,需要21000个元素(远远超过宇宙中估计的原子数)。然而,我们已经看到了一些递归深度与n.Java对递归深度的限制成比例的线性递归可能会破坏这种计算。
可以重新配置Java虚拟机,以便为嵌套方法调用提供更大的空间。这是通过在启动Java时设置-Xss runtime选项来实现的,可以作为命令行选项,也可以通过IDE的设置来实现。但通常可以依赖递归算法的直觉,而不是使用方法调用来表示必要的重复,而是更直接地重新实现它。我们只讨论这样一种方法来结束这一章。
5.2 消除尾递归
递归算法设计方法的主要优点是,它允许我们简洁地利用许多问题中存在的重复结构。通过使我们的算法描述以递归的方式利用重复结构,我们通常可以避免复杂的案例分析和嵌套循环。这种方法可以导致更具可读性的算法描述,同时仍然相当有效。
然而,递归的有用性是以适度的代价来实现的。特别是,Java虚拟机必须维护跟踪每个嵌套调用状态的帧。当计算机内存处于高级状态时,派生递归算法的非递归实现是有益的。
一般来说,我们可以使用堆栈数据结构,通过人工调整递归结构的嵌套,而不是依赖解释器来将递归算法转换为非递归算法。虽然这只会将内存使用从预处理程序转移到堆栈,但我们可以通过存储所需的最小信息来进一步减少内存使用量。
更妙的是,某些形式的递归可以在不使用辅助内存的情况下被消除。其中一种形式被称为尾部递归 。如果从一个上下文中进行的任何递归调用是该上下文中的最后一个操作,则递归就是尾部递归,递归调用的返回值(如果有)由封闭递归立即返回。根据需要,尾部递归必须是线性递归(因为如果必须立即返回第一个递归调用的结果,则无法进行第二个递归调用)。
在本章演示的递归方法中,代码片段的二进制搜索方法和代码片段的reverseArray方法都是尾部递归的示例。我们的其他一些线性递归几乎类似于尾部递归,但技术上不是这样。例如,代码片段的阶乘方法不是尾部递归。最后是命令:
return n ∗ factorial(n−1);
这不是尾部递归,因为在递归调用完成后执行了一个额外的乘法运算,返回的结果不一样。出于类似的原因,代码片段的linearSum方法、代码示例中的幂方法以及fibonacciGood方法都不能作为尾部递归 。
尾部递归是特殊的,因为它们可以通过将主体封闭在循环中以进行重复,并通过将现有参数重新分配给这些值来用新参数替换递归调用,从而自动地非递归地重新实现。事实上,许多编程语言实现可以用这种方式转换尾部递归作为一种优化。
/** Returns true if the target value is found in the data array. */
public static boolean binarySearchIterative(int[ ] data, int target) {
int low = 0;
int high = data.length − 1;
while (low <= high) {
int mid = (low + high) / 2;
if (target == data[mid]) // found a match
return true;
else if (target < data[mid])
high = mid − 1; // only consider values left of mid
else
low = mid + 1; // only consider values right of mid
}
return false; // loop ended without success
}
作为一个具体的例子,我们的binarySearch方法可以重新实现,如代码示例所示。我们在while循环之前初始化变量low和high来表示数组的完整范围。然后,在循环的每个过程中,我们要么找到目标,要么缩小候选子射线的范围。在原始版本中进行递归调用binarySearch(data,target,low,mid−1),我们只需在新版本中替换high=mid−1,然后继续循环的下一个迭代。我们最初的基本情况条件low>high已被相反的循环条件所取代,而low<=high。在我们的新实现中,如果while循环结束时从未从内部返回true,则返回false以指定失败的搜索。
大多数其他的线性递归可以通过迭代非常有效地表达,即使它们不是形式上的尾部递归。例如,对于计算阶乘、计算斐波纳契数、求和数组元素或反转数组的内容,有一些简单的非递归实现。例如,代码示例提供了一个非递归方法来反转数组的内容(与下面代码的递归方法相比)。
/** Reverses the contents of the given array. */
public static void reverseIterative(int[ ] data) {
int low = 0, high = data.length − 1;
while (low < high) { // swap data[low] and data[high]
int temp = data[low];
data[low++] = data[high]; // post-increment of low
data[high−−] = temp; // post-decrement of high
}
}



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek “源神”启动!「GitHub 热点速览」
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· C# 集成 DeepSeek 模型实现 AI 私有化(本地部署与 API 调用教程)
· DeepSeek R1 简明指南:架构、训练、本地部署及硬件要求
· 2 本地部署DeepSeek模型构建本地知识库+联网搜索详细步骤