sicily 1563 GECKO

Description

During the rainy season, one of the walls in the house is infested with mosquitoes. The wall is covered by h × w square tiles, where there are h rows of tiles from top to bottom, and w columns of tiles from left to right. Each tile has 1 to 1000 mosquitoes resting on it.

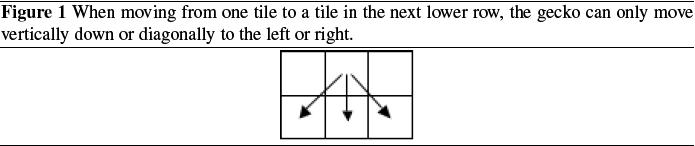
A gecko wants to eat as many mosquitoes as possible, subject to the following restrictions. It starts by choosing any tile in the top row, and eats the mosquitoes in that tile. Then, it moves to a tile in the next lower row, eats the mosquitoes on the tile, and so on until it reaches the floor. When it moves from one tile to a tile in the next lower row, it can only move vertically down or diagonally to the left or right .

Given the values of h and w, and the number of mosquitoes resting on each tile, write a program to compute the maximum possible number of mosquitoes the gecko can eat in one single trip from the top to the bottom of the wall.

Input

The first line has two integers. The first integer h (1 <= h <= 500) is the number of rows of tiles on the wall. The second integer w (1 <= w <= 500)is the number of columns of tiles on the wall.  Next, there are h lines of inputs. The ith line specifies the number of mosquitoes in each tile of the top ith row. Each line has w integers, where each integer m (1 <= m <= 1000) is the number mosquitoes on that tile. The integers are  separated by a space character.

Output

The output file contains a single integer, which is the maximum possible number of mosquitoes the gecko can eat in one single trip from the top to the bottom of the wall.

Sample Input

6 5
3 1 7 4 2
2 1 3 1 1
1 2 2 1 8
2 2 1 5 3
2 1 4 4 4
5 7 2 5 1

Sample Output

 

32

分析：

本体是典型的DP类型题，每一层是一段状态，选优递推即可，相对简单而且直白。注意最后要求的是一层中的最优。当然也可以从后向前推，更省空间，这里不再优化。

代码：

// Problem#: 1563
// Submission#: 1907365
// The source code is licensed under Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
// URI: http://creativecommons.org/licenses/by-nc-sa/3.0/
// All Copyright reserved by Informatic Lab of Sun Yat-sen University
#include <iostream>
using namespace std;

#define MAX 500

int wall[MAX][MAX];
int move[3][2] = {{-1, -1}, {-1, 0}, {-1, 1}};
int dp[MAX][MAX] = {0};
int h, w;

inline bool judge(int x, int y) {
    return x >= 0 && x < h && y >= 0 && y < w;
}

inline int max(int x, int y) {
    int a, b, m;
    m = 0;
    for (int i = 0; i < 3; ++i) {
        a = x + move[i][0];
        b = y + move[i][1];
        if (judge(a, b) && dp[a][b] > m) m = dp[a][b];
    }
    return m;
}

int main() {
    cin >> h >> w;
    int re = 0;
    for (int i = 0; i < h; ++i)
        for (int j = 0; j < w; ++j)
            cin >> wall[i][j];
    for (int i = 0; i < w; ++i)
        dp[0][i] = wall[0][i];
    for (int i = 1; i < h; ++i) {
        for (int j = 0; j < w; ++j) {
            dp[i][j] = max(i, j) + wall[i][j];
        }
    }
    for (int i = 0; i < w; ++i)
        if (dp[h - 1][i] > re) re = dp[h - 1][i];
    cout << re << endl;
    return 0;
}