网络最大流 - 从入门开始，详细讲到实用易懂的 Dinic 算法

2019-02-22 更新

理解网络

一张网络，是一张带权有向图。比喻成输水系统可能好理解——

源头是大水库，想输出多少就输出多少。

但是，想要输出到目的地，需要经过中转点。中转点不产生新流量、也不私吞；接受多少流量，就同时输出多少流量。

点与点之间管道的容量（可以理解为水流量限制；注意“流量”指单位时间通过量，可以想象一下）是有限的；一条边上的流量不能超出其容量，容量很可能是有残余的。因为这些边上的限制，源头并不能无限输出。

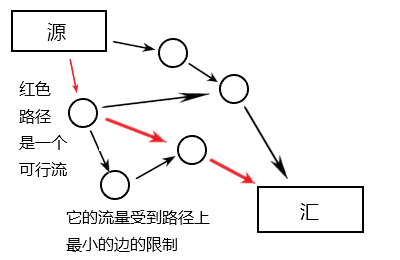
于是有的人就想要求出：这张网络运作起来的时候，总流量最大能有多少。由于容量限制比较复杂，似乎不容易规划一个最佳方案。

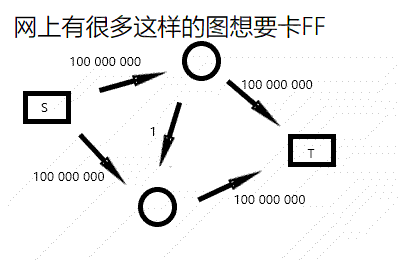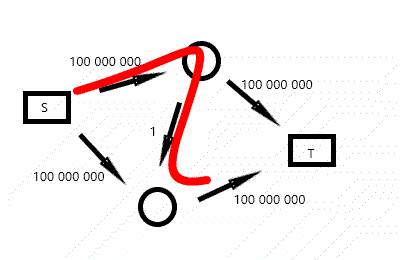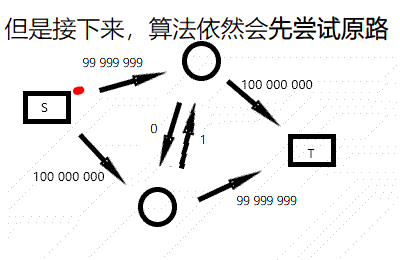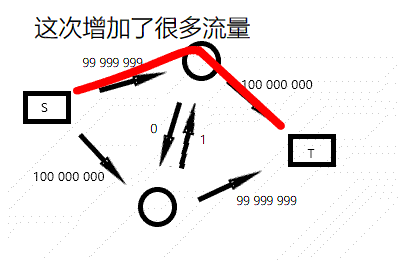
下面来了一张经典图和一只猴子。

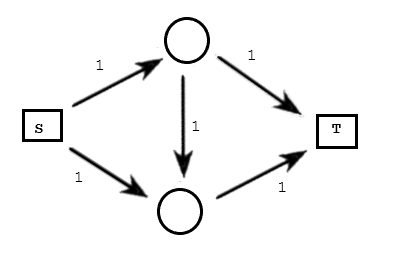
边上的数字是其容量限制。

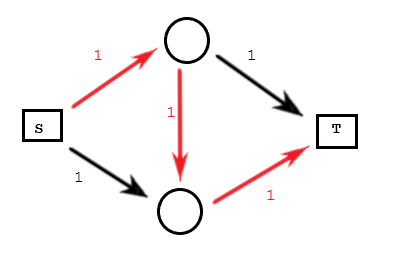
红色的路径，是猴子随便添加的一条可行流（电脑不能看见整张图，所以它跟猴子没啥区别）。这个时候总流量是 \(1\)。

然后猴子继续随机尝试。想要让水流通过下方的黑边，但接下来没法把这份流量传到 \(T\)。猴子决定吃水果去了。

现在水正在按照红色路径流动，流量只有 \(1\)，就没法操作了。但你凭借聪明才智，很容易发现这是一种糟糕的策略，只要开始的时候 \(S\) 沿着上下两条路走到 \(T\)，总流量就有 \(2\) 了。

机智的猴子决定回来暴搜所有流法，它能解决这种规模的数据就已经很满意了……当然我们有更好的方法：

在水顺着管子流过去的时候，添加一条反向边，边的容量等于此次流量，允许其它路径过来。啥玩意儿？

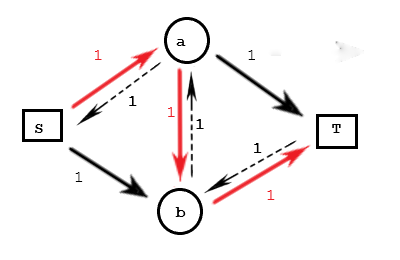
想象红色管子里这个水正在咕咕流动，就这个方向。网络中暗暗显现了它们对应的反向边。

这时候再次尝试找路。\(S\) 顺着下方管道给 \(b\) 传过去 \(1\) 流量。然后 \(b\) 找到了一条反向边流到 \(a\)？有点颠覆世界观啊。

不必理解成 \(b\) 流回 \(a\)，而可当作 \(a\) 的反悔。

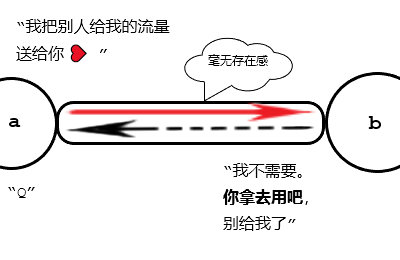
以点为主体进行考虑。\(a\) 看到源点向 \(b\) 给予 \(1\) 流量，于是 \(a\) 决定收回它给予的等量流量，拿去做别的事情，于是管道被空置了。

“我先前帮助 \(b\)，给他 \(1\) 流量流到终点去；现在源点跟他关系那么好，支援他 \(1\) 流量，使他足够维持输出，那我也要拿回那 \(1\) 流量，不流向他了！”

（其实你不拿回的话，\(b\) 就不平衡了）

于是，对中间的边，\(a\) 不进行输出。

当然，在算法运行的时候，“某次找到这条路并尝试输出、接下来某次找路时退回”的过程是存在的。退回方向的反向边（即原边）获得了 \(1\) 份新的残余容量，已经回到最早的状态了。\(a\) 收回流量后，它决定流向终点，网络又增加了 \(1\) 流量（原来的流量没有被破坏）。

从源点开始，顺着有流量的边，只要能找到一条能到达汇点的路（不管路径上是否有“退回”操作），就会使网络总流量增加，这种路叫增广路。上面是两次增广，然后就发现网络就没有增广路了，并且成果好像还不错。

---

最大流的算法

对一张网络，是不是只要不断找增广路（增广过程中记得提供退回操作的机会），直到找不到，就是网络最大流？

抱歉，这是真的。为什么呢？

...无数实践已经证明。

Part 1

一个网络正在按照猴子的计划流动。

于是猴子作了一个割。割是一个边集：这些边如果去掉，就会使图变成两个不相连的点集，一个点集 \(S\) 包含源点，一个点集 \(T\) 包含汇点。

原本 \(S\) 到 \(T\) 那几条边，它们的净流量（实际流量）称为 \(S\) 到 \(T\) 的净流量。注意，可能有水从 \(T\) 流向 \(S\)，它们对净流量是负的贡献。

对于这张网络，除了源点和汇点，其它点都是“流入多少，就流出多少”，没有实际贡献或收入。

汇点收到的流量，是 \(T\) 中所有点的综合作用；\(T\) 中的点本身（除了汇点），既不产生流量也不私藏流量，那么它们从哪里获得给汇点的流量呢？只能是 \(S\) 传过来的。所以，

• \(S\) 到 \(T\) 的净流量 = 源点输出 = 汇点收入 = 网络总流量

不管怎么构造割，都有这个结果，所以，

• 图上任何一种割的净流量 = 网络总流量

因为割的净流量不可能超过此割的总容量（当然啦），所以，

• 网络总流量 <= 图上任何一种割的容量

Part 2

经过猴子的调整，它的网络上没有增广路了。源点顺着残量网络到不了汇点了。

源点顺着残量网络能够到达的点，叫做点集 \(S\)（至少包含自己），剩下所有不能到达的点，叫做点集 \(T\)。则 \(S\) 连向 \(T\) 的边都没有残余容量（如果有残量边，\(S\) 也顺着这条边包含了对面的点）。

如果把 \(S\) 和 \(T\) 中间的边割断，那么这个割的净流量 = 这个割的容量（因为边上都没有残余容量了）。

又因为 Part 1 证的“网络总流量 = 任意一个割的净流量”，所以网络总流量 = 此割的容量（①）。

其实这很不容易做到的，因为 Part 1 证了“网络总流量 <= 图上任何一种割的容量”，所以“①”一定是面这个不等式的交界处。

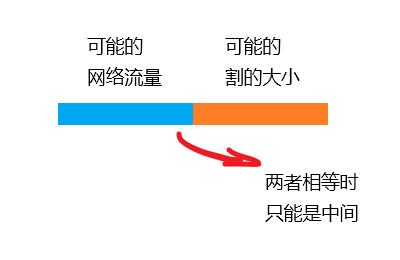
所以，这个网络流已经是众望所归。

一个总体的印象是：只要没有增广路，即顺着残量网络到不了汇点，就说明存在一个无残量的割，其净流量等于容量；因为网络总流量同时等于图上任何一个割的净流量，也就同时绝不会超过图上任何一个割的容量，所以当总流量 = 某割的容量时，已经没有比它更大的流，分号以前达到了这个条件，所以现在是最大流。

（还顺便证明了最大流 = 最小割）

增广路定理的证明其实很重要，它把网络最大流问题化简为：

不断找增广路就好了

但是考虑到每次流过去，反向边容量又增加了，提供太多的反悔机会，会死循环吗？

不会的。首先明确，最大流是有限的（当然）；而每次找增广路，总流量不会减少，只会增加（重申一下，一条边的“收回流量”操作并不会减少流量，毕竟收回的前提是对方获得支援；增加流量本身没有任何代价，只是有各边的容量限制着），在有限次增广后，总流量一定会达到最大值，然后找不到增广路，结束。

实现起来也有很多细节。

#include <cstdio>
#include <cstring>
#include <algorithm>
using std::min;

const int N = 10010, E = 200010;

int n, m, s, t;
int first[N];
int to[E], nxt[E], val[E]/*残余容量*/;
int cnt = 1;
//cnt初值1，第一条边的标号为2（二进制10），第二条是3（二进制11） 
//有啥好处呢？
//我们加入一条边时，紧接着加入它的反向边（初始容量0） 
//这两条边的标号就是二进制最后一位不相同，一个0、一个1
//所以要召唤 p 这条边的反向边，只需用 p ^ 1
//如果cnt初值为0，就做不到。当然初值-1也可以，略需改动

//关于图中真正的反向边，可能引起顾虑，应该让它们标号相邻？ 
//其实不用。该找到的增广路都会找到的 

bool vis[N];//限制增广路不要重复走点，否则很容易爆栈 
//兜一大圈走到汇点，还不如直接走到汇点

void addE(int u, int v, int w) {
	++cnt;
	to[cnt] = v;
	val[cnt] = w;
	nxt[cnt] = first[u];
	first[u] = cnt;
}
int dfs(int u, int flow) {
	//注意，在走到汇点之前，无法得知这次的流量到底有多少 
	if (u == t)
		return flow;//走到汇点才return一个实实在在的流量 
	
	vis[u] = true;
	for (int p = first[u]; p; p = nxt[p]) {
		int v = to[p];
		if (val[p] == 0 or vis[v])//无残量，走了也没用 
			continue;
		int res = 0;
		if ((res = dfs(v, min(flow, val[p]))) > 0) {
			//↑顺着流过去，要受一路上最小容量的限制
			val[p] -= res;//此边残余容量减小
			val[p ^ 1] += res;//以后可以顺着反向边收回这些容量，前提是对方有人了 
			return res;
		}
	}
	return 0;//我与终点根本不连通（依照残量网络），上一个点不要信任我
}
int main() {
	scanf("%d %d %d %d", &n, &m, &s, &t);
	for (int i = 1; i <= m; ++i) {
		int u, v, w;
		scanf("%d %d %d", &u, &v, &w);
		addE(u, v, w);
		addE(v, u, 0);//和正向边标号相邻
		//反向边开始容量为0，表示不允许平白无故走反向边
		//只有正向边流量过来以后，才提供返还流量的机会
	}
	int res = 0, tot = 0;
	while (memset(vis, 0, sizeof(vis)) and (res = dfs(s, 2e9/*水库很强*/)) > 0)
		tot += res;//进行若干回合的增广

	printf("%d\n", tot);
	return 0;
}

这种直接深搜找增广路的办法叫做 Ford-Fulkerson（FF）算法。

由于每次只找一条路，这条路还可能绕远路（可能经过 n 个点才到达汇点），而且增加流量是路上最小的权值，效率低，好像很容易被卡掉。但上面的代码能是通过模板题的，最慢一个点 500ms。

不过你可以看出，这个算法的复杂度和流量有关，令人担心。

Maximum Flow Faster Algorithm

我们还是有办法解决 FF 效率低的问题。

• 每次多路增广：u 点通过一条边，向 v 输出流量以后，v 会尝试到达汇点（到达汇点才真正增广），然后 v 返回实际增广量。这时，如果 u 还有没用完的供给，就继续尝试输出到其它边。

  但是要警惕绕远路、甚至绕回的情况，不加管制的话极易发生。怎么管？

• 源点顺着残量网络想要到达其它点，需要经过一些边对吧？按照经过的边数（即源点出发以后的距离）把图分层，即用 bfs 分层。每次尝试给予时，只考虑给予自己下一层的点，就可以防止混乱。

• 综合上面两条。每回合也是从源点出发，先按照当前残量网络分一次层，随后多路增广，尽可能增加流量。增广过程中，会加入一些反向边，这些反向边逆着层次图，本回合并不会走。所以还需要进入下一回合。一直到 bfs 分层时搜不到汇点（即残量网络断了）为止。

这是 Dinic 算法。如果懂 FF，这个算法也很块能懂。

可是它每次只按照 bfs 分层的固定方向进行增广，还能保证正确性吗？这个好理解。只要图中还有增广路（源点顺着残量网络到达汇点的路），bfs 分层就会搜索到汇点，于是增广就不会停止，最终也止于没有增广路的局面。

虽然从它“每次多路增广、绕弯少”能够大致体会它比 FF 快，但它保证会快吗？

...无数实践也已经证明。

要是把 Dinic 卡到上界的话，模板题都过不去了。

#include <cstdio>
#include <cstring>
#include <algorithm>
using std::min;

const int N = 10010, E = 200010;

int n, m, s, t, ans = 0;
int cnt = 1, first[N], nxt[E], to[E], val[E];
inline void addE(int u, int v, int w) {
	to[++cnt] = v;
	val[cnt] = w;
	nxt[cnt] = first[u];
	first[u] = cnt;
}
int dep[N], q[N], l, r;
bool bfs() {//顺着残量网络，方法是 bfs；这是个bool型函数，返回是否搜到了汇点 
	memset(dep, 0, (n + 1) * sizeof(int));//记得开局先初始化 

	q[l = r = 1] = s;
	dep[s] = 1;
	while(l <= r) {
		int u = q[l++];
		for(int p = first[u]; p; p = nxt[p]) {
			int v = to[p];
			if(val[p] and !dep[v]) {//按照有残量的边搜过去 
				dep[v] = dep[u] + 1;
				q[++r] = v;
			}
		}
	}
	return dep[t];//dep[t] != 0，就是搜到了汇点 
}
int dfs(int u, int in/*u收到的支持（不一定能真正用掉）*/) {
//注意，return 的是真正输出的流量
	if(u == t)
		return in;//到达汇点是第一个有效return 
	int out = 0;
	for(int p = first[u]; p and in; p = nxt[p]) {
		int v = to[p];
		if(val[p] and dep[v] == dep[u] + 1) {//仅允许流向下一层 
			int res = dfs(v, min(val[p], in)/*受一路上最小流量限制*/);
			//res是v真正输出到汇点的流量
			val[p] -= res;
			val[p ^ 1] += res;
			in -= res;
			out += res;
		}
	}
	if(out == 0)//我与终点（顺着残量网络）不连通 
		dep[u] = 0;//上一层的点请别再信任我，别试着给我流量
	return out;
}
int main() {
	scanf("%d %d %d %d", &n, &m, &s, &t);
	for(int i = 1; i <= m; ++i) {
		int u, v, w;
		scanf("%d %d %d", &u, &v, &w);
		addE(u, v, w);
		addE(v, u, 0);
	}
	while(bfs()) 
		ans += dfs(s, 2e9);
	printf("%d\n", ans);
	return 0;
}

注意理解多路增广：虽然一个点要枚举所有出边，但实质仍然是 dfs，过程图类似于树。

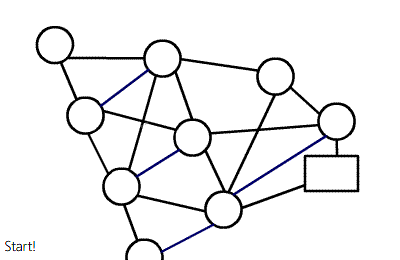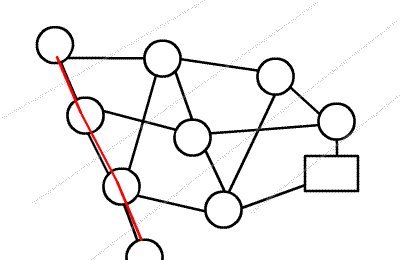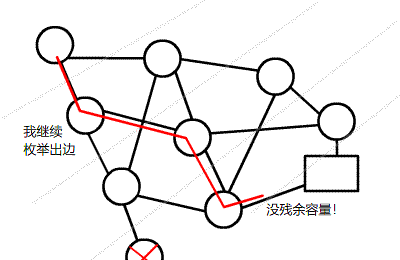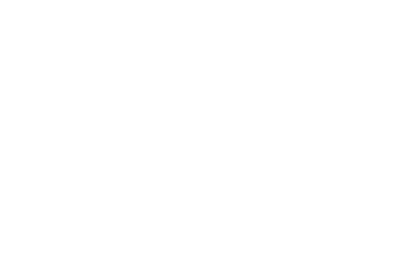
复杂度可能的证明：《浅谈基于分层思想的网络流算法》 P4 ~ P14。但是这里关于增广次数的证明中，某个结论好像忽略了一种情况。

Dinic 能应付绝大多数网络流题目了，大概因为网络流题目主要考察建模能力吧。当然最大流还有更高效的算法。

---

更新日志：

2019-02-22 代码和注释改动。