对称二叉树

问题 F: 对称二叉树

时间限制: 1.000 Sec  内存限制: 256 MB

题目描述

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：
1. 二叉树；
2. 将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值，节点外的 id 表示节点编号。

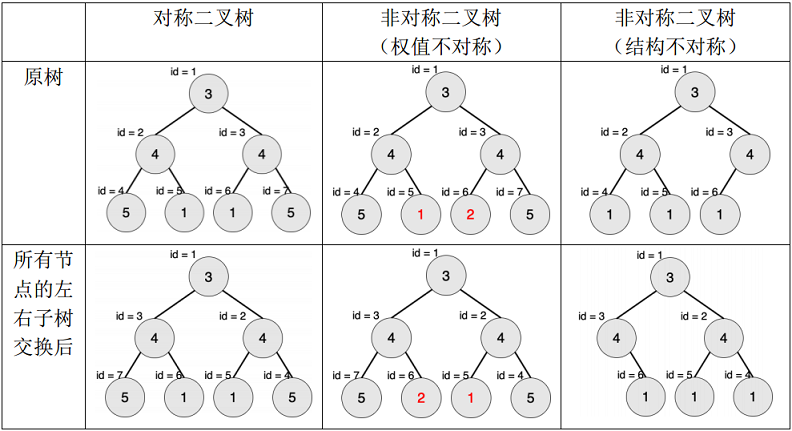
现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数最多。请输出这棵子树的节点数。
注意：只有树根的树也是对称二叉树。 本题中约定， 以节点  T  为子树根的一棵 “子树”指的是：节点  T  和它的全部后代节点构成的二叉树。

输入

第一行一个正整数 n，表示给定的树的节点的数目，规定节点编号 1 .. n，其中节点 1 是树根。

第二行 n 个正整数，用一个空格分隔，第 i 个正整数 v_i代表节点 i 的权值。

接下来 n 行，每行两个正整数 l_i, r_i，分别表示节点 i 的左右孩子的编号。如果不存在左 / 右孩子，则以 -1 表示。两个数之间用一个空格隔开。

输出

共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

样例

输入1  

2

1 3

2 -1

-1 -1

输出1  

1

---

输入2  

10

2 2 5 5 5 5 4 4 2 3

9 10

-1 -1

-1 -1

-1 -1

-1 -1

-1 2

3 4

5 6

-1 -1

7 8

输出2  

3

提示

【输入输出样例 1 说明】

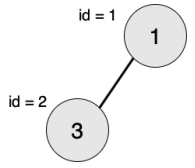
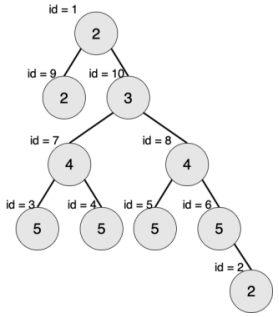
最大的对称二叉子树为以节点 2 为树根的子树，节点数为 1。
【输入输出样例 2 说明】

最大的对称二叉子树为以节点 7 为树根的子树，节点数为 3。

【数据规模与约定】
共 25 个测试点。
v_i ≤ 1000。
测试点 1 .. 3, n ≤ 10，保证根结点的左子树的所有节点都没有右孩子，根结点的右 子树的所有节点都没有左孩子。
测试点 4 .. 8, n ≤ 10。
测试点 9 .. 12, n ≤ 10^5，保证输入是一棵“满二叉树” 。
测试点 13 .. 16, n ≤ 10^5，保证输入是一棵“完全二叉树”。
测试点 17 .. 20, n ≤ 10^5，保证输入的树的点权均为 1。
测试点 21 .. 25, n ≤ 10^6。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 1。

树的深度：树中节点的最大层次称为树的深度。

满二叉树：设二叉树的深度为 h，且二叉树有 2h-1 个节点，这就是满二叉树。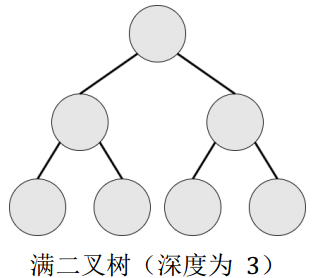

完全二叉树：设二叉树的深度为  h，除第  h  层外，其它各层的结点数都达到最大个数，第  h  层所有的结点都连续集中在最左边，这就是完全二叉树。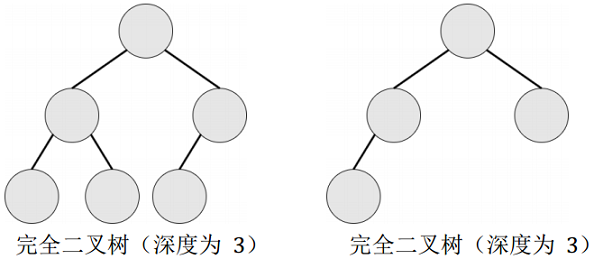

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e7;
int n;
int v[maxn],l[maxn],r[maxn];
 
int ans ;
int is ;
 
void f(int x,int y){    
    if(x == -1 && y == -1){             
        return ;
    }
    if(x == -1 || y == -1 || v[x] != v[y]){ 
        is = 0;                         
        return ;
    }
    f(l[x],r[y]);                                               
    f(r[x],l[y]);                   
}
 
int cnt(int x){
    int k=1;
    if(l[x] != -1 ){
        k += cnt(l[x]); 
    }
    if(r[x] != -1 ){
        k += cnt(r[x]);
    }   
    return k;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&v[i]);
    }
    for(int i=1;i<=n;i++){
        scanf("%d%d",&l[i],&r[i]);}
    for(int i=1;i<=n;i++){
         is = 1;
        f(l[i],r[i]);
        if(is){ 
            ans = max(ans,cnt(i));
        }
    }
    cout<<ans<<endl;
    return 0;
}