算法基础一

认识时间复杂度：

时间复杂度为，在一个算法的流程中，常数操作数量的指标，这个指标叫做O（字母O而非数字零），big O。具体为 ，如果常数操作数量的表达式中，只要高阶项，不要低阶项，也不要高阶项系数，剩下的部分记为f(N)，那么该算法的时间复杂度为O(f(N))。

比如：我们求一个数组中的最大值

求数组中的最大值，一般思路是把数组遍历一遍，设置一个中间变量max来记录最大值，中间用来取数组中的数的操作，赋值操作，这些操作成常数操作（所谓常数操作，指的是完成这个操作的时间和数据量无关，它是一个固定的值）。在数组中的寻址代价是big O(1)的，即常数操作，拿到的这个数和max进行比较，比较的这个操作也是常数操作。从0位置遍历到n-1位置，我们花费的总代价为：n*常数操作。即认为完成这些操作的代价为C*n（其中C为常数），我们就说它是big O(n)的算法。

一 冒泡排序（Bubble Sort）：

冒泡排序是一种典型的交换排序算法，通过交换数据元素的位置进行排序。

时间复杂度O(N^2)，额外的空间复杂度O(1)，实现可以做到稳定性。

• 基本思想

冒泡排序的基本思想是：从无序序列头部开始，进行两两比较，根据大小交换位置，直到最后将最大（小）的数据元素交换到了序列的尾部，从而成为有序序列的一部分；下一次继续这个过程，直到所有数据元素都排好序。

算法的核心在于每次通过两两比较交换位置，选出剩余无序序列里最大（小）的数据元素放到尾部。

下面我们来看一下冒泡排序的简单例子（将序列按从小到大排）：

假设有一个无序序列  { 5， 1， 7， 2， 9 }

第一趟排序：通过两两比较，找到第一大的数值 9 ，将其放在序列的末尾。{ 1， 5， 2， 7， 9 }

第二趟排序：通过两两比较，找到第二大的数值 7 ，将其放在序列的倒数第二位。{ 1， 2， 5， 7， 9 }

第三趟排序：通过两两比较，找到第三大的数值 5 ，将其放在序列的倒数第三位。{ 1， 2， 5， 7， 9 }

...

所有元素已经有序，排序结束。 

 

其实，流程大致是：

　　　　　　　　　　在0-（n-1)进行操作

　　　　　　　　　　在0-（n-2)进行操作

　　　　　　　　　　在0-（n-3)进行操作

　　　　　　　　　　...

直到遍历结束，序列最终有序。

• 代码转换

假设要对一个大小为 n 的无序序列进行升序排序（即从小到大排列）。 

（1）因为遍历第一次需要找到 0-（n-1）上最大的值，第二次遍历需要找到 0 - （n-2）上最大的值，因此，需要设置一个外循环，用来进行遍历；

（2）在遍历过程中，需要进行两两比较（第一次需要从0-（n-2）进行两两比较，第二次需要从0-（n-3）进行两两比较），因此，需要设置一个内循环来进行两两之间的比较；

（3）单独考虑特殊情况，数组长度为0或者小于2（即1）时不作处理。

以下是java代码的实现：

public class BubbleSort {

    @Test
    public void bubbleSort(int arr[]) {
        //数组为空或者只有一个元素，直接返回
        if(arr==null || arr.length<2) {
            return;
        }
        else {
            //end代表每次将0-end元素中最大的数放到end上,直到第一个元素
            for(int end=arr.length-1; end>=0; end--) {
                //从0-（end-1）开始两两比较
                for(int i=0; i<end; i++) {
                    if(arr[i]>arr[i+1])
                        swap(arr,i,i+1);
                }
            }
        }
    }
    //交换两个数的方法
    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

 

 

 以上就是冒泡排序的简单介绍。

二 对数器

下面我们来简单介绍一个对数器的概念及其使用。

对数器是用来测试代码正确性的，我们在找不到合适的oj系统（online judge）测试自己的代码时，可以自己写一个对数器对代码进行测试。

设计对数器的一般步骤为：

1. 一个你要测试正确性的方法a； 
2. 实现一个绝对正确即使复杂度不好的方法b； 
3. 实现一个随机样本产生器； 
4. 实现比对的方法； 
5. 把方法a和方法b比对很多次来验证方法a是否正确 
6. 如果有一个样本使得比对出错，打印样本分析是哪个方法出错 
7. 当样本数量很多时比对测试依然正确，可以确定方法a已经正确

在设计对数器的时候，一定要保证程序的绝对正确，可能时间复杂度很坏，但是只要正确即可。在验证的时候可以挑一些你认为极端的情况进行正确性的验证，这样能够快速进行比对。

我们通过一个例子来简单了解一下：

1. 我们要验证的方法a

public void bubbleSort(int arr[]) {
        //数组为空或者只有一个元素，直接返回
        if(arr==null || arr.length<2) {
            return;
        }
        else {
            //end代表每次将0-end元素中最大的数放到end上,直到第一个元素
            for(int end=arr.length-1; end>=0; end--) {
                //从0-（end-1）开始两两比较
                for(int i=0; i<end; i++) {
                    if(arr[i]>arr[i+1])
                        swap(arr,i,i+1);
                }
            }
        }
    }
    //交换两个数的方法
    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

2. 实现一个绝对正确即使复杂度不好的方法b

    // 一个绝对正确的方法，调用java自带的排序方法
    public void rightMethod(int[] arr) {
        Arrays.sort(arr);
    }

 

3. 实现一个样本产生器

//产生测试数据  
//Math.random()  ->  double[0,1)
2 public static int[] testData(int len,int value){  
3     int arr[] = new int[len];  
4     for (int i = 0; i < arr.length; i++) {  
5     arr[i] = (int) ((value+1)*Math.random()-    (value+1)*Math.random());  
6         }  
7     return arr;  
8 } 

 

4. 实现比对的方法

//判断两个数组是否相等
public static boolean isEqual(int[] arr1, int[] arr2) {
    if((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null))
        return false;
    if(arr1 == null && arr2 == null)
        return true;
    if(arr1.length != arr2.length)
        return false;
    for(int i = 0;i < arr1.length;i++) {
        if(arr1[i] != arr2[i])
            return false;
    }
    return true;
}

5.把方法a和方法b比对很多次来验证方法a是否正确 

6.如果有一个样本使得比对出错，打印样本分析是哪个方法出错 
7.当样本数量很多时比对测试依然正确，可以确定方法a已经正确

public static void main(String[] args) {  
    int len = 10;//测试数组长度  
    int val = 100;//测试数据范围  
    int times = 500000;//测试数据量  
    boolean isOK = true;  
    for (int i = 0; i < times; i++) {  
        int arr[] = testData(len, val);  
        int arr1[] = Arrays.copyOf(arr, len);  
        int arr2[] = Arrays.copyOf(arr, len);  
        bubbleSort(arr1);  
        systemSort(arr2);  
        if( ! isEqual(arr1, arr2)){  
            printArr(arr1);  
            printArr(arr2);  
            isOK = false;  
            break;  
        }  
    }  
    System.out.println(isOK);  
} 

 至此，一个对数器就实现了，正确的使用对数去对于学习和工作来说是有很大帮助的。

三 选择排序

选择排序（Selection sort）同样也是最经典最简单的排序算法之一，它的特点就是简单直观。

排序的原理：在0-（n-1）（元素总数目为n）里面选择最小（大）的一个元素，放在0号位置；

　　　　　　在1-（n-1）里面选择最小（大）的一个元素，放在1号位置；

　　　　　　...

选依次循环，直到排序完成。

和上面介绍的冒泡排序不同的是，选择排序只需要交换一次。

下面我们来看代码：

public class SelectionSort{
    
    public static void selectionSort(int[] arr) {
        if(arr==null || arr.length<2) {
            return ;
        }
        //此处我们选择最小的进行选择排序
        for(int i=0; i<arr.length; i++) {
            int minIndex = i;
            for(int j=i+1; j<arr.length-1; j++) {
                minIndex = arr[j]<arr[minIndex] ? j : minIndex;
            }
            swap(arr, i, minIndex);
        }
    }
    
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    
}

 四 插入排序

插入排序原理：它是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。我们假设第一个元素排好，之后的元素对排好的部分从后向前比较并逐一移动。

下面我们来看代码：

五 时间复杂度，空间复杂度的简单比较以及master公式

插入排序，选择排序，冒泡排序的时间复杂度都是big (N²) ，空间复杂度big O(1)（因为是有限的几个变量,big O(1)就是常数的意思）；

而归并排序，快速排序，堆排序的时间复杂度是big O(N*logN)，空间复杂度：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　归并排序：big O(N)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　快速排序：big O(logN)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　堆排序：big O(1)

 

master公式（也称主方法）是用来利用分治思想来计算时间复杂度，分治思想中使用递归来求解问题分为三步走，分别为分解、解决和合并，主方法的表现形式：

T [n] = aT[n/b] + f (n)（直接记为T [n] = aT[n/b] + T (N^d)）

其中 a >= 1 and b > 1 是常量，其表示的意义是：n表示问题的规模，a表示递归的次数也就是生成的子问题数，b表示每次递归是原来的1/b之一个规模，f（n）表示分解和合并所要花费的时间之和。

解法：

1. 当d<log_ba时，时间复杂度为O(n^(logb a))
2. 当d=log_ba时，时间复杂度为O((n^d)*logn)
3. 当d>log_ba时，时间复杂度为O(n^d)

六 归并排序

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

归并排序介绍：

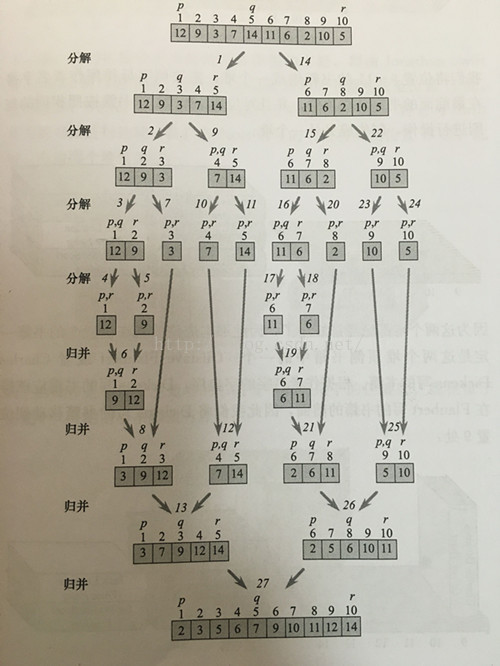
上图是归并排序的一个大致的过程。归并排序的思想是分治思想，具体做法是：

把一个数组分为两部分，左半部分和右半部分，然后分别将这两个部分再分解，直到各个部分长度为1,然后进行合并，合并的过程中始终保持左边小右边大（即左半部分和右半部分分别从小到大排好序），然后再将左半部分和右半部分进行合并（在合并的过程中创建一个辅助数组用来存放排好序的数组，最后将排好序的数组赋值给原数组），归并排序结束。

下面我们来看Java代码的实现：

 

public class MergeSort {

    
    public static void mergeSort(int[] arr) {
        if(arr==null || arr.length<2)
            return;
        mergeprocess(arr, 0, arr.length-1);//递归调用
    }
    
    public static void mergeprocess(int[] arr, int L, int R) {
        if(L==R)
            return;
        int mid = L + (R-L)/2;
        mergeprocess(arr, L, mid);
        mergeprocess(arr, mid+1, R);
        merge(arr, L, R);
    }
    
    public static void merge(int[] arr, int L, int R) {
        int[] help = new int[R-L+1];
        int mid = L + (R-L)/2;
        int p = L;
        int q = mid+1;
        int i = 0;
        while(p<=mid && q<=R) {//循环比较加入到辅助数组
            if(arr[p]<=arr[q])
                help[i++] = arr[p++];
            if(arr[p]>arr[q])
                help[i++] = arr[q++];
        }
        
        while(p<=mid) {//必有一个没循环结束
            help[i++] = arr[p++];
        }
        while(q<=R) {
            help[i++] = arr[q++];
        }
        
        //辅助数组复制给原数组
        for(i=0; i<help.length; i++) {
            arr[L+i] = help[i];
        }
        
    }
    
    //swap method
    public static void swap(int i, int j, int[] arr) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    //for test
    public static void printArray(int[] arr) {
        if(arr==null)
            return;
        for(int i=0; i<arr.length; i++) 
            System.out.print(arr[i]);
        System.out.println();
    }
    public static void main(String[] args) {
        int[] arr = {6,2,9,3,8,1,2};
        mergeSort(arr);
        printArray(arr);
    }
        
}

 

归并排序的使用——小和问题

利用归并排序的分治思想来求解小和问题，在左半部分（以左半部分为例）合并的过程中，如果排序时不交换（即左边<右边），则产生一个小和；在左半部分和右半部分合并的过程中，左半部分中的数如果小于右半部分的数，则利用右半部分的下标（因为右半部分已经排好序，故右半部分中的数（大于左半部分的数），则小和的个数是——右半部分的数的末尾数字下标-比对的右半部分的数对应的下标）即可得到左右部分合并过程中的小和数。

例子：
　　[1,3,4,2,5]
　　1左边比1小的数，没有；
　　3左边比3小的数，1；
　　4左边比4小的数，1、3；
　　2左边比2小的数，1；
　　5左边比5小的数，1、3、4、2；
所以小和为1+1+3+1+1+3+4+2=16

下面我们来看Java代码实现：

package Sort;

public class SmallSum {

    public static int smallSum(int[] arr) {
        if(arr==null || arr.length<2)
            return 0;
        return mergeSort(arr, 0, arr.length-1);
    }
    
    public static int mergeSort(int[] arr, int L, int R) {
        if(L==R)
            return 0;
        int mid = L + (R-L)/2;
        return mergeSort(arr, L, mid) +
              mergeSort(arr, mid+1, R)+
              merge(arr, L, mid, R);
    }
    
    public static int merge(int[] arr, int L, int mid, int R) {
        
        int[] help = new int[R-L+1];
        int res = 0;
        int p = L;
        int q = mid+1;
        int i = 0;
        while(p<=mid && q<=R) {
            if(arr[p]<arr[q]) {
                res += arr[p]*(R-q+1);
                help[i++] = arr[p++];
            }
            if(arr[p]>=arr[q]) {
                res += 0;
                help[i++] = arr[q++];
            }
        }
        while(p<=mid) {
            help[i++] = arr[p++];
        }
        while(q<=R) {
            help[i++] = arr[q++];
        }
        
        for(i=0; i<help.length; i++) {
            arr[L+i] = help[i];
        }
        return res;
    }
    
    //for test
    public static void printArray(int[] arr) {
        if(arr==null)
            return;
        for(int i=0; i<arr.length; i++) 
            System.out.print(arr[i]);
        System.out.println();
    }
    
    public static void main(String[] args) {
        int[] arr = {1,3,2,5,2};
        int res = smallSum(arr);
        System.out.println(res);
    }

}