跟我一起学算法——二项堆
1.二叉堆(Binary Heap)、二项堆、斐波那契堆(简称Fib堆)的比较:
相同:
- 都是可归并堆(Mergeable Heap);
- 它们都支持5个基本操作(创建、插入、查找最小值、抽取最小值、合并堆)和2个扩展操作
(结点减值、结点删除)。
不同:
- 二叉堆是一种结点有序的完全二叉树,可采用数组结构存储,通过数组下标索引结点,分最大
堆和最小堆。 二项堆和Fib堆都是最小堆。 - 二项堆由二项树组成,结构比二叉堆复杂,但其堆合并操作的时间复杂度较好。当堆合并操作
较多时,可使用二项堆。反之,使用二叉堆即可。
![在这里插入图片描述]()
2. 二项树
2.1 定义
仅包含一个结点的有序树是一棵二项树(B_0树)。二项树B_k由两棵B_{k-1}树组成,其中一
棵B_{k-1}树的根作为另一棵B_{k-1}树根的最左孩子(k≥0)。
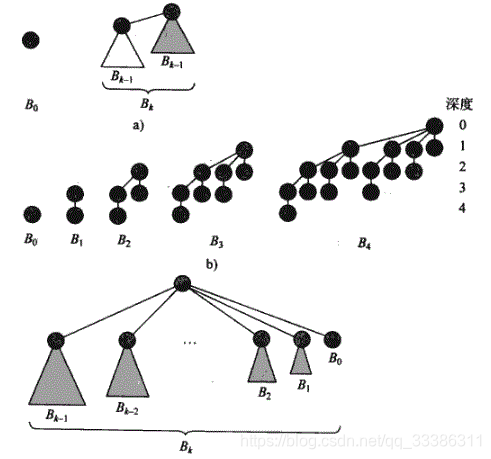
2.2 二项树B_k的性质
- 结点数 n = 2
- 树高为 k = lgn
- 深度为i处有k!/(i!(k-i)!)个结点(k>=i>=0)。
- 根的度最大为k,若根的孩子从左到右编号为k-1,k-2,…,1,0,则孩子i恰好是子树B_i的根。
proof:主要依靠B_k与B_{k-1}间的关系
- 2^{k-1} + 2^{k-1} = 2^
- k-1+1 = k
- 即证D(k,i) = D(k-1,i-1) + D(k-1,i)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-x0BE2UNK-1582727656770)(img/binomialHeap-math1.png)]
3. 二项堆
3.1 定义
它是由一系列二项树组成的集合,满足以下性质:
堆中每一颗二项树都满足最小堆性质。堆中度为k的树是唯一的 => n个结点的二项堆中最多有
lgn上界 + 1课二项树
3.2 数据结构
-
根表 root list
head[H]->B_0->B_2->B_3
根表是单链表,它链接所有二项树的根结点,且按度的递增顺序链接。 -
结点 node
每个结点包含5个域:
key:数据
指针p:指向父结点
degree(度):孩子个数
child:指向最左孩子
sibling:指向右兄弟
class Node():
"""
class of the node in the heap
provide functions to the binomial tree
"""
def __init__(self, key = None):
self.p = None # point to parent
self.key = key # value
self.degree = 0 # count of the children
self.child = None # point to child of the left
self.sibling = None # point to the right brother
def link_tree(self, other):
"""
other -> subtree of self.
"""
other.parent = self
other.sibling = self.child
self.child = other
self.degree += 1
3.3 操作
3.3.1 五个基本操作
-
创建空堆
-
取最小值:由于二项树满足最小堆性质,所以遍历根表即可。
-
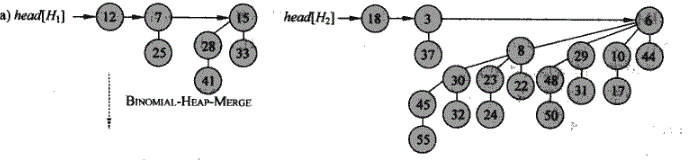
合并两个二项堆
step1:按照二项树的度递增的顺序合并两个根表。
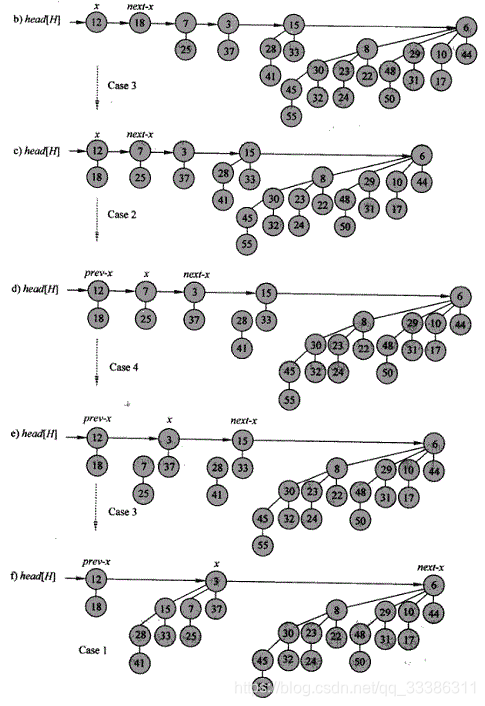
step2:根表调整,以满足度的唯一性。用三个辅助指针(per、p、after)将度重复的树合并。
由于step1合并后的根表中,度相同的树最多有两颗,所以会出现以下几种情况:
case1:三个指针所指二项树根都存在,且度不同 => 指针后滑,进入case3或结束。
case2:per为空,p.degree = after.degree,且after.sibling存在 =>指针后滑,进入case4。
case3:case1或case2不成立,若pre为空,则一定有p.degree = after.degree => 根据degree
合并p和after所指二项树,after后滑,进入case2 或 case1
case4:三个指针所指二项树根都存在,且度相同 =>根据degree合并p和after所指二项树,after
后滑,进入case3。时间复杂度分析:
- 合并根表 O(lgn)
- 根表调整,遍历新根表O(lgn)
- 合并操作的时间复杂度为O(lgn),优于二叉堆的O(n)
![]()
![在这里插入图片描述]()
def _merge_rootlist(self, heap2):
"""
merge two root list and keep increasing order in degree.
"""
p1 = self.head
p2 = heap2.head
if not p1: # p1 = None
return heap2.head
if not p2: # p2 = None
return self.head
if p1.degree <= p2.degree:
p = p1
p1 = p1.sibling
else:
p = p2
p2 = p2.sibling
head = p
while p1 and p2:
if p1.degree <= p2.degree:
p.sibling = p1
p1 = p1.sibling
else:
p.sibling = p2
p2 = p2.sibling
p = p.sibling
if p2:
p.sibling = p2
else:
p.sibling = p1
return head
def _union(self, heap2):
"""
step1: merge two root list and keep increasing order in degree.
step2: adjust root(merge) to keep the unique of the degree in all
binomial trees.
use three point to adjust the heap: pre , p , after
"""
if heap2 is None:
return
if self.head is None:
self.head = heap2.head
self.size = heap2.size
return
# step1
head = self._merge_rootlist(heap2)
print("merge root list")
self.print_rootlist()
# step2 use three point to adjust the heap
if not head:
print("merge rootlist error")
return
pre = None
p = head
after = head.sibling
while after:
# case 1 / case 2 , point + 1
if p.degree != after.degree or (after.sibling is not None and
after.sibling.degree == p.degree ):
pre = p
p = after
# case 3, merge p and after into p
elif p.key <= after.key:
# update point
p.sibling = after.sibling
# merge two tree, p.child = after
p.link_tree(after)
else:
# after.degree == p.degree, after.sibling = None, p.key>after.key
# => update head ,link(after,p),over!
if pre == None:
head = after
# upfate pre.sibling = after, link(after,p)
else:
pre.sibling = after
after.link_tree(p)
p = after
after = p.sibling
self.head = head
self.size += heap2.size
return
- 插入结点x
将x放入一个空堆H2中,将H和H2合并。
时间复杂度为O(lgn)
def insert(self, node):
"""
insert a node into a null heap.
1. node->new heap (heap2)
2. union(self, heap2)
"""
h = BinomialHeap()
h.head = node
self.union(h)
self.size += 1
- 抽取最小值结点
step1:遍历根表查最小值结点z。
step2:在根表中删除结点z,并把z的孩子"逆放"到一个空堆H2中。所谓逆放,即使H2满足二项堆根
表中树根的度递增的顺序。
step3:将H和H2合并。
时间复杂度O(lgn)
def extract_min_node(self):
self._extract_min_node()
return
def _extract_min_node(self):
size = self.size
min_node, pre_min = self.min()
self.extract(min_node, pre_min)
self.size = size - 1
return
def extract(self, node, pre_node):
if node == None:
return
# del min node in the root list
if pre_node==None:
self.head = min_node.sibling
else:
pre_node.sibling = node.sibling
# if the minimum node has no child
if(node.child == None):
return
# if the node has subtrees, then inesrt them into a new heap, and union this new heap with old heap.
new_heap = BinomialHeap()
# insert the subtrees in reverse order
p = node.child
list_root = []
while p.sibling != None:
p.parent = None
list_root.append(p)
p = p.sibling
list_root.append(p)
while list_root != []:
p = list_root.pop(-1)
new_heap.insert(p)
# union
self.union(new_heap)
return
3.3.2 两个扩展操作
- 减值(减少结点z的key)
z减值后自底向上迭代比较,直到孩子结点的值大于父结点。类似冒泡。
时间复杂度;O(lgn)
def _decrease_key(self,node,key):
if node == None or node.key <= key:
print("node or key err")
return
node.key = key
x = node
p = node.p
# bubble
while p is not None and p.key > x.key:
t = p.key
p.key = x.key
x.key = t
x = p
p = p.p
return
- 删除结点z
step1:对z进行减值操作,将z的值减为最小值。
step2:对z所在二项树的树根执行抽取操作。
时间复杂度:O(lgn)
参考
《算法导论》



 浙公网安备 33010602011771号
浙公网安备 33010602011771号