跟我一起学算法——动态规划
1. 步骤
- 描述问题的最优解(optimal solution)结构特征
- 递归定义最优解值
- 自底向上 计算最优解值
- 从已计算得到的最优解值信息中构造最优解
2. 要素
最优子结构和重叠子问题
最优子结构性质是指一个问题的最优解中所包含的所有子问题的解都是最优的。
动态规划避开了递归时,重复计算相同子问题的过程,对每个子问题只解一次,而后将其保存在一个
表格中,当再次需要的时候,查表获取。
3. 装配线调度
-
最优子结构性质:如果问题的解是最优的,则所有子问题的解也是最优的。在这里,描述为最优
路径的子路径也是最优的。
最优子结构证明:剪枝法
∵如果子路径P1从开始到S1,j-1不是最优的,那么一定存在一条从开始到S1,j-1的更优子路径P2,
当用P2去替换原子路径P1后,将得到一条比原路径更优的路线,这与假设从开始到S1,j是一条最
优路线矛盾。
∴子路径P1一定也是最优的 -
递归定义最优路线的最快时间
最快时间 f=min(f1[n]+x1,f2[n]+x2)
要得到f值,需要计算fi[j]的每个值
f1[j]=min{f1[j-1]+a(1,j),f2[j-1]+t(2,j-1)+a(1,j)}
f2[j]=min{f2[j-1]+a(2,j),f1[j-1]+t(1,j-1)+a(2,j)}
递归初始值:f1[1]=e1+a(1,1); f2[1]=e2+a(2,1) -
先确定此问题的底,然后再自底向上计算最优解值,O(n)
-
构造最优解结构(输出最优路线)
4. 矩阵链乘
给定一个矩阵序列<A1,A2,…,An>,其中矩阵Ai的维数为Pi-1×Pi,要求计算A1×A2×…×An矩阵链乘的
乘法次数最少?
- 最优子结构
设矩阵A_i 的维数是 P_(i-1) * P_i,输入序列为P0,P1...Pn,则
假设子问题A_ij的解(A_i*A_(i+1)…A_j)是一个最优解,则在Aij中一定存在一个 最佳分裂点k(i≤k<j),
使得子链A_ik和A_k+1,j的解(A_i*A_(i+1)…A_k)和(A_(k+1)…A_j)也是最优的。 - 递归定义最优解值
规模为n^2的辅助结构m[i,j]存放子链A_ij=(A_iA_(i+1)…A_j)的乘法次数,m[1,n]表示所有n个矩
阵链乘的乘法次数。m[i,j] 的规模为矩阵上三角=O(n^2)
i=j时,m[i,j] = 0
i<j时,m[i,j] = min(m[i,k]+m[k+1,j]+ P_(i-1)*P_k*P_j ),i<=k<j - 自底向上计算最优解值
辅助结构s[i,j]用于记录最佳分裂点k的位置
递归计算链长分别为2到n的矩阵链的最佳组合,长链计算依赖短链的最佳计算结果。
时间复杂度O(n^3)
matrix-chain-order(P)
n=length[p]-1
for i=1 to n
m[i,i]=0
for l=2 to n //l为链长
for i=1 to n-l+1 //具有n-l+1个链长为l的组合
j=i+l-1
m[i,j]=∞
for k=i to j-1 //找最佳分裂点k
q=m[i,k]+m[k+1,j]+ P_(i-1)*P_k*P_j
if q<m[i,j]
m[i,j]=q
s[i,j]=k //记录最佳分裂点
return m and s
- 输出最优解结构
5. 最长公共子序列(Longest Common Subsequece)
令给定序列X={x1,x2,…xm},另一序列Z={z1,z2,…zk}是X的子序列必须满足:X的下标中存在一个
严格的递增序i1<i2<…<ik,使得对所有的j均有Xij=Zj(1≤j≤k)。换句话说,子序列是原序列删除
若干个元素所得。
对于序列X和Y,序列Z如果既是X的子序列又是Y的子序列,则Z是X和Y的公共子序列。
- LCS问题最优子结构性质
令X={x1,x2,…xm},Y={y1,y2,…yn}为二个序列,子序列Z={z1,z2,…zk}是X和Y的一个最长公共
子序列,则:
- if xm=yn then zk=xm=yn且Zk-1是Xm-1和Yn-1的LCS
- if xm≠yn,则有两个子问题,X_m-1 和 Y的LCS 及 X 和 Y_m-1的LCS。
- 递归定义LCS值
令C[i,j]存放子序列Xi和Yj的LCS长度,则:
- i or j=0时,C[i,j] = 0
- i,j>0 and xi=yj时, C[i,j] = C[i-1,j-1]+1
- i,j>0 and xi≠yj时, C[i,j] = max
- 自底向上计算LCS值
O(mn)
b[i,j]用于存放xi和yi的LCS是哪种情况,=0表示情况1,=1和-1分别表示X_m-1和Y的LCS及X和Y_m-1的LCS
def LCS_Length(x,y):
m=len(x)
n=len(y)
for i in range(m):
c[i][0]=0
for j in range(n):
c[0][j]=0
for i in range(1,m):
for j in range(1,n):
if x[i]=y[j]:
c[i][j] = c[i-1][j-1] + 1
b[i][j] = 0
elif c[i-1][j]>=c[i][j-1]:
c[i][j]=c[i-1][j]
b[i][j] = 1
else:
c[i][j]=c[i][j-1]
b[i][j] = -1
return c,b
- 根据c和b输出LCS
改进:直接由x[i] ?= y[j],c[i-1][j],c[i][j-1]判断,可以取缔b[i,j]。
def printLcs(c,x,y,i,j)
if i == 0 or j == 0:
return
if x[i] == y[j]:
printLcs(c,x,y,i-1,j-1)
print(x[i])
elif c[i-1][j]>=c[i][j-1]:
printLcs(c,x,y,i-1,j)
else
printLcs(c,x,y,i,j-1)
6. 最优二叉查找树(Optimal Binary Search Tree)
对于单个关键字的查找,在红黑树上查找时间为O(lgn),但若查找的是一系列关键字且每个关键字
的查找频度值不同,此时从整体来看红黑树不能产生最少的时间。
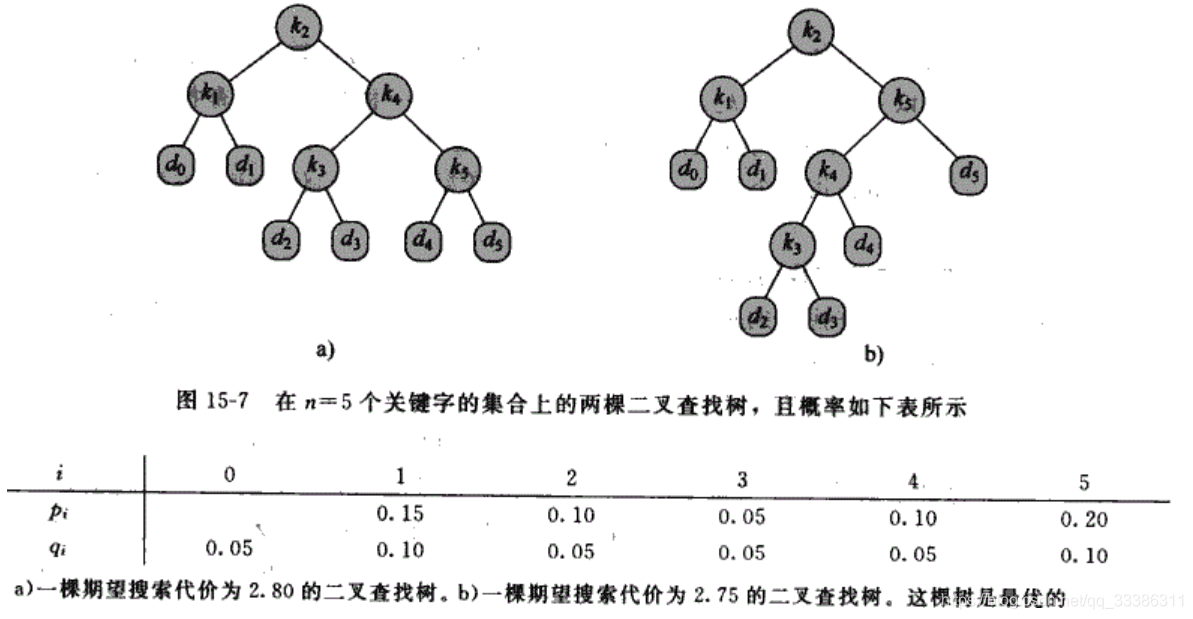
令n个不同的关键字集K={k1,k2,...,kn},其中k1<k2<…<kn;
pi:检索关键字ki的概率
令d0,d1,…,dn表示不在关键字集K中的虚拟(dummy)关键字;
d0:小于k1的所有关键字;dn:大于kn的所有关键字;
di:介于ki和ki+1之间的所有关键字(i=1,2,…,n-1)
qi:检索关键字di的概率
关键字检索只有二种状态 :成功检索:找到关键字ki,概率为pi; 不成功检索:找到关键字di,概率为qi;
总概率和 pi(i=1->n)+pj(i=0->n)=1.
定义E(搜索代价)= (depth(k_i)+1)*p_i(i=1->n) + (depth(d_i)+1)*q_i(i=0->n) =
1 + depth(k_i)*p_i(求和i=1->n) + depth(d_i)*q_i(求和i=0->n)
E最小的二叉查找树 称为 最优BST。
- 最优子结构
如果Tr是一棵以kr为根且包含ki,…,…,kj的OBST,那么包含关键字ki,…kr-1的左子树Tl及包含
关键字kr+1,…,kj的右子树Tr也是OBST。思想类似于找矩阵链的最佳分裂点。 - 递归定义最优解值
令e[i,j]为包含关键字ki,…,kj的OBST平均检索代价,则e[1,n]为所求解,其中i≥1,j≤n且j≥i-1
当j=i-1时,e[i,j]=q_i-1
当j>=i时,e[i,j] = min{e[i,r-1]+e[r+1,j]+w(i,j)};其中
w(i,j)=p_k(求和k=i->j)+q_k(求和k=i-1 -> j); - 自底向上计算最优解值
O(n^3)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号