后缀数组（SA）

后缀数组（SA）

感觉会有很多写错或写不清楚的地方，读者发现问题可以评论或右侧 QQ 联系我，感谢！

约定

“ 后缀 \(i\) ” 表示以第 \(i\) 个字符开头的后缀。

\(a[i]\) 表示字符串 \(a\) 的第 \(i\) 位，\(a[l, r]\) 表示 \(a\) 中位置 \(l \sim r\) 的子串。

一个字符串从第 \(1\) 位开始，第 \(n\) 位结束。

两个字符串的大小关系定义如下：

1. \(a\) 与 \(b\) 为同一字符串，则 \(a = b\)。

2. \(a\) 是 \(b\) 的真前缀，则 \(a < b\)。

3. 若不满足 1.2. 则一定存在最小的 \(i\) 满足 \(a[i] \not = b[i]\) 则 \(a, b\) 的大小关系由 \(a[i]\) 和 \(b[i]\) 的大小关系确定。

定义

后缀数组主要求两个数组：\(sa\) 和 \(rk\)。

其中，\(sa[i]\) 表示将所有后缀排序后第 \(i\) 小的后缀编号，\(rk[i]\) 表示后缀 \(i\) 的排名，简单来说，\(sa[i]\) 表示排名 \(i\) 的是谁，\(rk[i]\) 表示后缀 \(i\) 排名第几。

显然，这两个数组满足 \(rk[sa[i]]=sa[rk[i]]=i\)。以下是一个 \(sa\) 和 \(rk\) 的例子：

做法

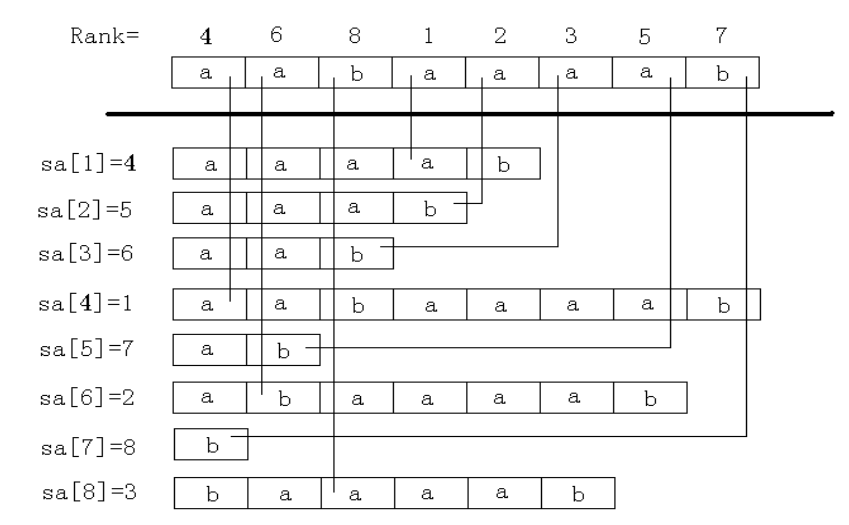
\(\mathcal O(n^2 \log n)\) 做法

把所有后缀处理出来，用 sort 进行排序，每次比较为 \(\mathcal O(n)\) 则总时间复杂度为 \(\mathcal O(n^2 \log n)\)。

\(\mathcal O(n \log^2 n)\) 做法

需要用到倍增思想。令 \(rk_w[i]\) 表示 $ \forall x\in[1, n], s[x, \min(x + w - 1, n)]$ 中 \(s[i, \min(i + w-1, n)]\) 的排名，则对于 \(rk_{2w}[i]\) 我们可以通过以 \(rk_w[i]\) 为第一关键字，\(rk_w[i + w]\) （$ i+w>n$ 则视为无穷小）为第二关键字，进行排序即可求出 \(rk_{2w}[i]\) 的值。求出所有后缀排名会进行以上操作 \(O(\log n)\) 次，若使用 sort 进行排序则每次排序 \(\mathcal O(n\log n)\) ，则时间复杂度为 \(\mathcal O(n\log^2 n)\)。

以下为倍增示意图：

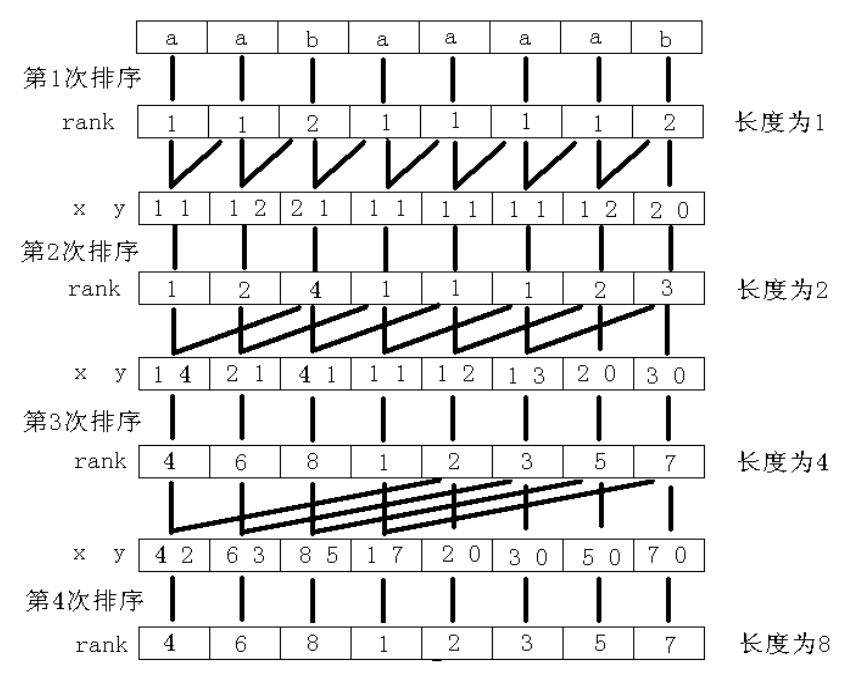
\(\mathcal O(n \log n)\) 做法

发现瓶颈是排序，如果能做到 \(\mathcal O(n)\) 排序，就能做到 \(\mathcal O(n \log n)\) 了，考虑到排序的值域为 \(\mathcal O(n)\)，并且是一个双关键字的排序，所以我们可以使用基数排序将排序优化到 \(\mathcal O(n)\)。

这里介绍一下基数排序。

基数排序的原理是将待排序的元素拆分为 \(k\) 个关键字，以此以 \(k\) 关键字、\(k - 1\) 关键字、……、\(1\) 关键字进行排序，最后就能得到排序后的结果，以下是一个例子：

如果以计数排序为每次关键字排序的内层排序，则时间复杂度为 \(\mathcal O(kn + \sum\limits_{i=1}^k w_i)\) 其中，\(w_i\) 为第 \(i\) 层关键字的值域。

对应到倍增做法中的排序，\(k=2\)，\(w_1, w_2\) 为字符集大小，则排序复杂度则可看作 \(\mathcal O(n)\)，故最终后缀排序就可以做到 \(\mathcal O(n \log n)\)。

#include <bits/stdc++.h>
const int N = 1e6 + 10;
char s[N]; int n, m, k;
int cnt[N], sa[N], sec[N], rk[N];

inline void Csort()
{
	for (int i = 1; i <= m; ++ i)
		cnt[i] = 0;
	// 清零桶
	for (int i = 1; i <= n; ++ i)
		cnt[rk[i]] ++;
	// 将第一关键字压入桶中
	for (int i = 2; i <= m; ++ i)
		cnt[i] += cnt[i - 1];
	// 记个前缀和方便求排名
	for (int i = n; i >= 1; -- i)
		sa[cnt[rk[sec[i]]] --] = sec[i];
	// 对于第一关键字相同的数对来说
	// 其排名区间已经确定，我们只需通过第二关键字来确定其特定的排名
	// 我们从后到前枚举第二关键字的排名，则此时对应数对的排名就是对应排名区间的最后一个
	// 再将对应排名区间的右区间 -1 
	// 表示接下来枚举到的 第一关键字 相同的数对的排名区间改变了
}

int main()
{
	scanf("%s", s + 1);
	n = strlen(s + 1), m = 'z';
	// n, m 分别代表 s 长度以及字符集大小

	for (int i = 1; i <= n; ++ i)
		sec[i] = i, rk[i] = s[i];
	// sec[i] 表示第二关键字排名为 i 的编号
	// 初始时并无第二关键字，所以按照顺序排序
	// rk[i] 表示第一关键字中编号为 i 的排名
	// 初始时即为 s[i] 的字符大小
	// sa[i] 表示排名为 i 的编号

	// 需要注意，rk[i] 中相同串的排名会相同
	// sa[i] 中相同的串排名不会相同，会根据位置来具体排名（越靠前排名越前）
	Csort();

	for (int w = 1; w <= n; w *= 2)
	{
		// w 为当前倍增到的长度
		int num = 0;
		for (int i = n - w + 1; i <= n; ++ i)
			sec[++ num] = i; 
		// [n - w + 1, n] 无第二关键字，故令其关键字排名靠前
		for (int i = 1; i <= n; ++ i)
			if (sa[i] > w) sec[++ num] = sa[i] - w;
		// 从小到大枚举排名，判断此时这个串是否能作为其他串的第二关键字
		// 若能作为其他串的第二关键字，则对应编号为 sa[i] - w
		Csort(); std::swap(sec, rk); num = 0;
		// 第一第二关键字都已经求出，进行基数排序即可
		// 基数排序之后，sa 数组已经求出，我们需要用其更新 rk 数组
		// sec 数组已经没用，rk 数组需要更新，暂时用 sec 储存 rk 数组
		for (int i = 1; i <= n; ++ i)
			rk[sa[i]] = (sec[sa[i]] == sec[sa[i - 1]] 
				&& sec[sa[i] + w] == sec[sa[i - 1] + w]) ? num : ++ num;
		// 按照第一关键字排名从小到大枚举
		// 依次更新 rk 数组
		m = num;
		// 更新关键字值域大小
	}
	for (int i = 1; i <= n; ++ i)
		printf("%d ", sa[i]);
	return 0;
}

\(\mathcal O(n)\) 做法

有 SA-IS 和 DC3 做法，这里暂不介绍（一般用不到）。

应用

循环同构问题

循环同构：当字符串 \(s\) 中可以选定一个位置 \(i\) 满足：\(s[i,n] + s[1,i - 1] = t\) ，则称 \(s\) 与 \(t\) 循环同构，例如 \(\mathtt{abcdd}\)，与这个字符串循环同构的串有 \(\mathtt{abcdd}\)、\(\mathtt{bcdda}\)、\(\mathtt{cddab}\)、\(\mathtt{ddabc}\)、\(\mathtt{dabcd}\)，

给出一个字符串，我们需要知道与其字符串循环同构的串的排名。Link

将字符串 \(s\) 复制一份成 \(ss\)，求其后缀数组即可。

在字符串 \(s\) 中找子串 \(t\)（在线）

在线的含义是 \(s\) 给出，\(t\) 只在询问时给出。

将 \(s\) 的后缀数组求出，在其后缀数组中二分寻找 \(t\)（是否存在），\(q\) 组询问，时间复杂度 \(\mathcal O(|s| \log |s| + q \times |t| \log |s|)\)，当然，想找出 \(t\) 在 \(s\) 中所有出现的位置也是可以做的，但是 KMP 显然可以做到更优。

从字符串首尾取字符最小化字典序

给你一个字符串，每次从首或尾取一个字符组成字符串，问所有能够组成的字符串中字典序最小的一个。Link

一个简单的想法是暴力 \(\mathcal O(n)\) 判断选首还是选尾，这样最差是 \(\mathcal O(n ^2)\) 的，我们考虑将反串拼接在原串后，中间加个从未出现过的字符，这样，就可以 \(\mathcal O(1)\) 判断选首还是选尾，就能 \(\mathcal O(n\log n)\) 解决此题。

height 数组

LCP：两个字符串 \(s, t\) 的 LCP 表示最长相同前缀。

下文的 \(\operatorname {lcp}(l, r)\) 表示 \(s[l, n]\) 与 \(s[r, n]\) 的 LCP。

height 数组定义如下：

\[\operatorname {height}[x]=\begin{cases}\operatorname{lcp}(sa[x], sa[x - 1])&x > 1\\0&x=1\end{cases} \]

height 数组可以 \(\mathcal O(n)\) 求出，需要一个引理：\(\operatorname{height}[rk[i]] \geq \operatorname{height}[rk[i - 1]] - 1\)

证明如下：

1. 若 \(\operatorname{height}[rk[i - 1]] \leq 1\)，上述式子显然成立，因为 \(\operatorname{height}[rk[i - 1]] - 1 \leq 0\)。
2. 若 \(\operatorname{height}[rk[i - 1]] > 1\)，令后缀 \(i-1\) 为 \(aBC\)（\(B\) 长度为 \(\operatorname{height}[rk[i - 1]]-1\)，后面会用到），则后缀 \(i\) 为 \(BC\)，后缀 \(sa[rk[i-1]-1]\) 为 \(aBD(D < C)\)，我们可以推出后缀 \(sa[rk[i-1]-1]+1=BD\)，则后缀 \(sa[rk[i-1]-1]+1\) 一定排在 \(i\) 之前，故 \(\operatorname {lcp}(i, sa[rk[i] - 1]) \geq |B|=\operatorname{height}[rk[i - 1]]-1 \Rightarrow \operatorname {height}[rk[i]] \geq \operatorname{height}[rk[i - 1]]-1\)。

int LstHeight = 0;
for (int i = 1; i <= n; ++ i)
{ 
    // 按照 rk 从小到大求
	if (LstHeight) LstHeight --;
    // 从上一个状态继承下来
	while (s[sa[rk[i]] + LstHeight] == s[sa[rk[i] - 1] + LstHeight])
		LstHeight ++; // 求出对应的 height
	height[rk[i]] = LstHeight;
}

height 数组的应用

两子串最长公共前缀

给出一个定理：

\[\operatorname {lcp}(sa[l], sa[r])=\min_{i=l+1}^r \operatorname {height}[i] \]

要证明这个定理，我们首先证明一个引理：

​ 对于任意的 \(1 \leq l < k < r \leq n\)，\(\operatorname {lcp}(sa[l], sa[r])=\min \{\operatorname {lcp}(sa[l], sa[k]), \operatorname{lcp}(sa[k], sa[r]) \}\)

证明如下：

1. 设 \(p=\min \{\operatorname {lcp}(sa[l], sa[k]), \operatorname{lcp}(sa[k], sa[r]) \}\)，则有 \(\operatorname {lcp}(sa[l], sa[k]) \geq p,\operatorname{lcp}(sa[k], sa[r])\geq p \Rightarrow\) \(s[sa[l], sa[l] + p-1]=\) \(s[sa[k], sa[k]+p-1] = s[sa[r], sa[r] + p-1]\)，可以得到结论 \(\operatorname {lcp}(sa[l], sa[r]) \geq p\)。
2. 再设 \(\operatorname {lcp}(sa[l], sa[r]) =q > p\)，则有 \(s[sa[l], sa[l] + q - 1] = s[sa[r], sa[r] + q - 1]\)，由于 \(p=\min \{\operatorname {lcp}(sa[l], sa[k]), \operatorname{lcp}\) \((sa[k], sa[r]) \}\)，故 \(s[sa[l] + p - 1 + 1] \not=\) $ s[sa[k] + p - 1 + 1]$ 或 \(s[sa[r] + p - 1 + 1] \not= s[sa[k] + p - 1 + 1]\)，令 \(x=s[sa[l] + p - 1 + 1],y=s[sa[k]+p-1+1],z=s[sa[r] + p - 1 + 1]\)，因为 \(l < k < r\) 所以 \(x \leq y \leq z\)，又考虑到 \(q > p \Rightarrow x=z \Rightarrow x=y=z\) 与上文矛盾，故 \(q > p\) 不成立，可以得到结论 \(\operatorname {lcp}(sa[l], sa[r])\leq p\)。

由 1. 2. 可得：对于任意的 \(1 \leq l < k < r \leq n\)，\(\operatorname {lcp}(sa[l], sa[r])=\min \{\operatorname {lcp}(sa[l], sa[k]), \operatorname{lcp}(sa[k], sa[r]) \}\)

有了这个引理，证明上文的定理就很容易了，证明如下：

1. 当 \(r - l = 1\) 或 \(r-l=2\) 时，显然成立。
2. 设 \(r-l=m\) 时成立，当 \(r-l=m+1\) 时，由引理可知 \(\operatorname{lcp}(sa[l], sa[r])=\min\{\operatorname{lcp}(sa[l], sa[l + 1]), \operatorname{lcp}(sa[l + 1], sa[r])\}\) 考虑到 \(r-(l+1) = m\leq m\) 所以有 \(\operatorname{lcp}(sa[l], sa[r])=\min\{\operatorname{lcp}(sa[l], sa[l + 1]), \min\limits_{i=l+2}^r \operatorname {height}[i])\}=\min\limits_{i=l+1}^r \operatorname {height}[i]\)，根据数学归纳法，上述定理成立。

有了这个定理，求任意子串的 LCP 就可以转化为 RMQ 问题。

比较一个字符串的两个子串大小关系

需要比较的是 \(s[a, b]\) 和 \(s[c, d]\) 的大小关系。

1. 若 \(\operatorname {lcp} (a, c) \geq \min \{ b-a+1,d-c+1\}\)，则两者的大小关系由长度关系得到，即 \(b-a+1<d-c+1 \Leftrightarrow s[a, b] < s[c, d]\)。
2. 否则，两者的大小关系由 \(rk\) 数组确定，即 \(rk[a] < rk[c] \Leftrightarrow s[a, b] < s[c, d]\)。

不同子串数量

考虑容斥，子串我们看作后缀的前缀（非常常见的套路），总子串个数为 \(\dfrac{n \times (n-1)}{2}\)，如果按照后缀排序的顺序枚举后缀，每次新增的子串就是除了与上一个后缀的 LCP 剩下的前缀，也就是说，容斥要减去的就是当前的 height 数组。

所以，不同子串数量为：

\[\dfrac{n \times (n-1)}{2} - \sum_{i=2}^n \operatorname{height}[i] \]

出现至少 k 次的子串的最大长度

出现至少 \(k\) 也就代表着后缀排序之后，至少连续 \(k\) 个后缀的 LCP 含有这个子串，所以，求出 height 数组之后，找出每相邻的 \(k-1\) 个 height 数组的最小值的最大值，单调队列 \(\mathcal O(n)\) 即可（瓶颈在求后缀数组 \(\mathcal O(n\log n)\)，故用线段树啥的也行）。

参考文献

1. oi-wiki
2. [2004]后缀数组 by. 徐智磊
3. [2009]后缀数组——处理字符串的有力工具 by. 罗穗骞