深度学习正则化--L0、L1、L2正则化

概念

L0正则化的值是模型参数中非零参数的个数。

L1正则化表示各个参数绝对值之和。

L2正则化标识各个参数的平方的和的开方值。

 

先讨论几个问题：

1）实现参数的稀疏有什么好处吗？

一个好处是可以简化模型，避免过拟合。因为一个模型中真正重要的参数可能并不多，如果考虑所有的参数起作用，那么可以对训练数据可以预测的很好，但是对测试数据就只能呵呵了。另一个好处是参数变少可以使整个模型获得更好的可解释性。

2）参数值越小代表模型越简单吗？

是的。为什么参数越小，说明模型越简单呢，这是因为越复杂的模型，越是会尝试对所有的样本进行拟合，甚至包括一些异常样本点，这就容易造成在较小的区间里预测值产生较大的波动，这种较大的波动也反映了在这个区间里的导数很大，而只有较大的参数值才能产生较大的导数。因此复杂的模型，其参数值会比较大。

 

L0正则化

根据上面的讨论，稀疏的参数可以防止过拟合，因此用L0范数（非零参数的个数）来做正则化项是可以防止过拟合的。

从直观上看，利用非零参数的个数，可以很好的来选择特征，实现特征稀疏的效果，具体操作时选择参数非零的特征即可。但因为L0正则化很难求解，是个NP难问题，因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似，比L0容易求解，并且也可以实现稀疏的效果。

 

L1正则化

L1正则化在实际中往往替代L0正则化，来防止过拟合。在江湖中也人称Lasso。

L1正则化之所以可以防止过拟合，是因为L1范数就是各个参数的绝对值相加得到的，我们前面讨论了，参数值大小和模型复杂度是成正比的。因此复杂的模型，其L1范数就大，最终导致损失函数就大，说明这个模型就不够好。

 

L2正则化

L2正则化可以防止过拟合的原因和L1正则化一样，只是形式不太一样。

L2范数是各参数的平方和再求平方根，我们让L2范数的正则项最小，可以使W的每个元素都很小，都接近于0。但与L1范数不一样的是，它不会是每个元素为0，而只是接近于0。越小的参数说明模型越简单，越简单的模型越不容易产生过拟合现象。

L2正则化江湖人称Ridge，也称“岭回归”

 

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择

L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

 

假设有如下带L1正则化的损失函数： 

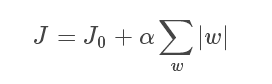
其中J0是原始的损失函数，加号后面的一项是L1正则化项，α是正则化系数。注意到L1正则化是权值的绝对值之和，J是带有绝对值符号的函数，因此J是不完全可微的。机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。当我们在原始损失函数J0后添加L1正则化项时，相当于对J0做了一个约束。令L等于正则化项，则J=J0+L，此时我们的任务变成在L约束下求出J0取最小值的解。考虑二维的情况，即只有两个权值w1和w2，此时L=|w1|+|w2|对于梯度下降法，求解J0的过程可以画出等值线，同时L1正则化的函数L也可以在w1w2的二维平面上画出来。如下图：

 

 
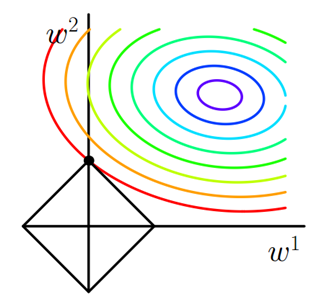
图1 L1正则化

图中等值线是J0的等值线，黑色方形是L函数的图形。在图中，当J0等值线与L图形首次相交的地方就是最优解。上图中J0与L在L的一个顶点处相交，这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w)(w1,w2)=(0,w)。可以直观想象，因为LL函数有很多『突出的角』（二维情况下四个，多维情况下更多），J0J0与这些角接触的机率会远大于与LL其它部位接触的机率，而在这些角上，会有很多权值等于0，这就是为什么L1正则化可以产生稀疏模型，进而可以用于特征选择。

而正则化前面的系数αα，可以控制LL图形的大小。αα越小，LL的图形越大（上图中的黑色方框）；αα越大，LL的图形就越小，可以小到黑色方框只超出原点范围一点点，这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。

类似，假设有如下带L2正则化的损失函数： 

 

 

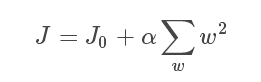
同样可以画出他们在二维平面上的图形，如下：

 

 
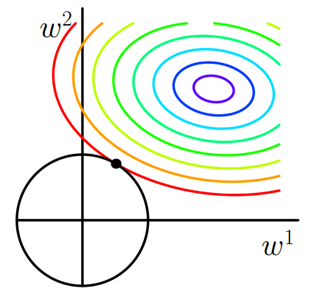
图2 L2正则化

二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此J0与L相交时使得w1或w2等于零的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。