AC 自动机——trie 树与 KMP 算法的结合体

默认所有字符串的下标从 \(1\) 开始。

梗概与实现

如果是单一的模式串和字符串进行匹配，KMP 算法自然可以派上用场。但如果有多个模式串呢？

对每个模式串都跑一遍 KMP？如果有 \(n\) 个模式串，求解 \(nxt[]\) 的时间复杂度为 \(O(\sum\limits_{i = 1}^n |p_i|)\)，而因为进行了 \(n\) 次匹配，所以匹配的时间复杂度为 \(O(n |s|)\)，也就是 \(O(n^2)\) 量级的时间复杂度了。并且 \(nxt[]\) 只作用于单个模式串，在多个模式串的情况下还是会出现资源的浪费。

有什么优化方案呢？AC 自动机。

如题，AC 自动机是 trie 树和 KMP 算法的结合体，算法梗概是将所有的模式串存入一个 trie 树中，并处理出与 KMP 中的 \(nxt[]\) 功能类似的 \(fail[]\) 数组，通过 \(fail[]\) 极大提高匹配效率。

举例，给定模式串为 she、he、her、say、shr，则建起来的 trie 树应该长这样（其中标黄表示该结点是某个模式串的末字符）：

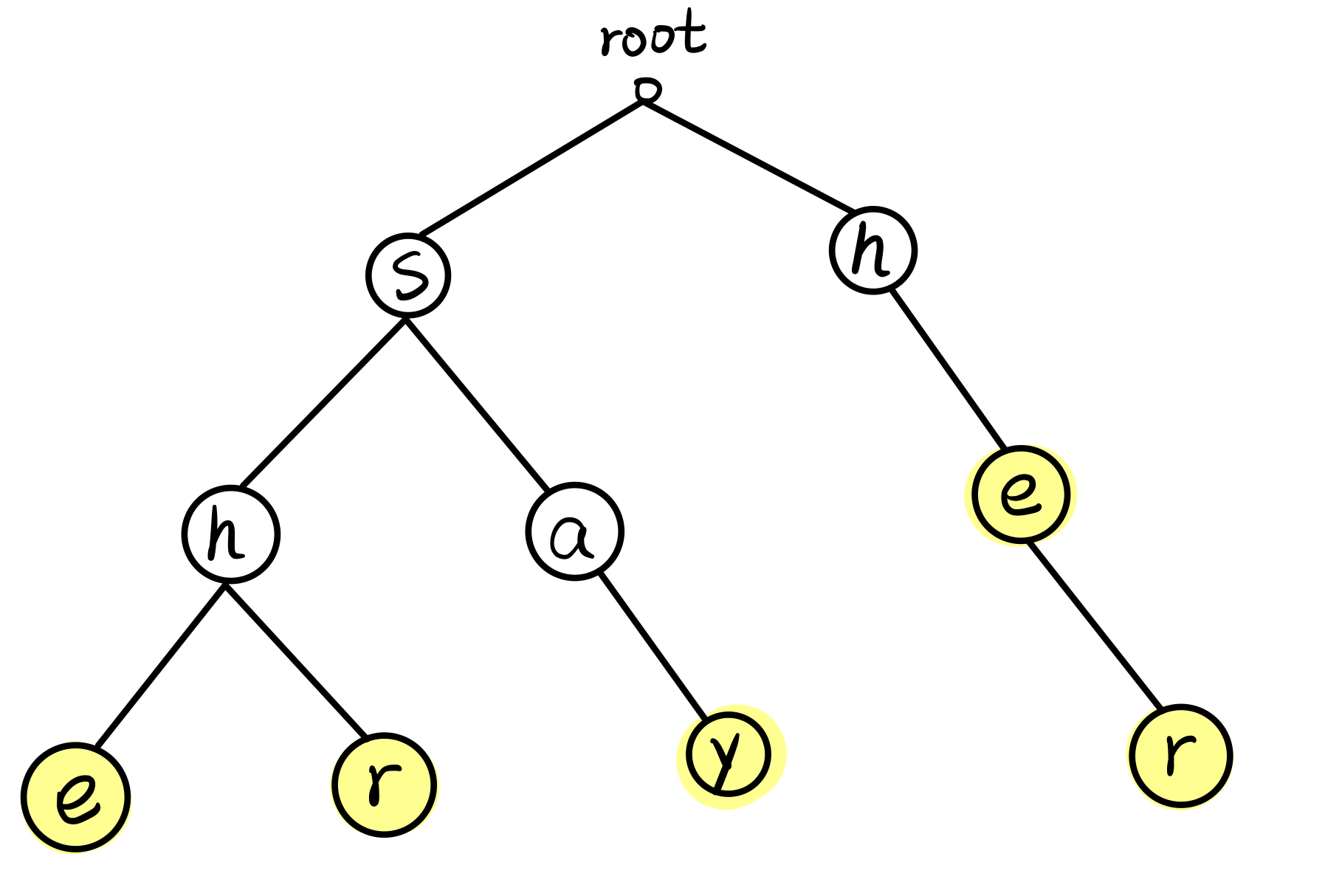
那么我们想想加入 \(fail[]\) 后，这个图应该长什么样子。

假设我们现在匹配完左侧的 e 结点，却发现下一个字符无法与 e 的子结点中的任意一个字符匹配（根本就没有怎么匹配），此时，我们已经确定当前字符与 e 匹配，上一字符与 h 匹配，从效率的角度出发，应该跳到右侧 h 下的 e，让下一个字符与 r 比对。

据此，可以画出来加上 \(fail[]\) 后的图：

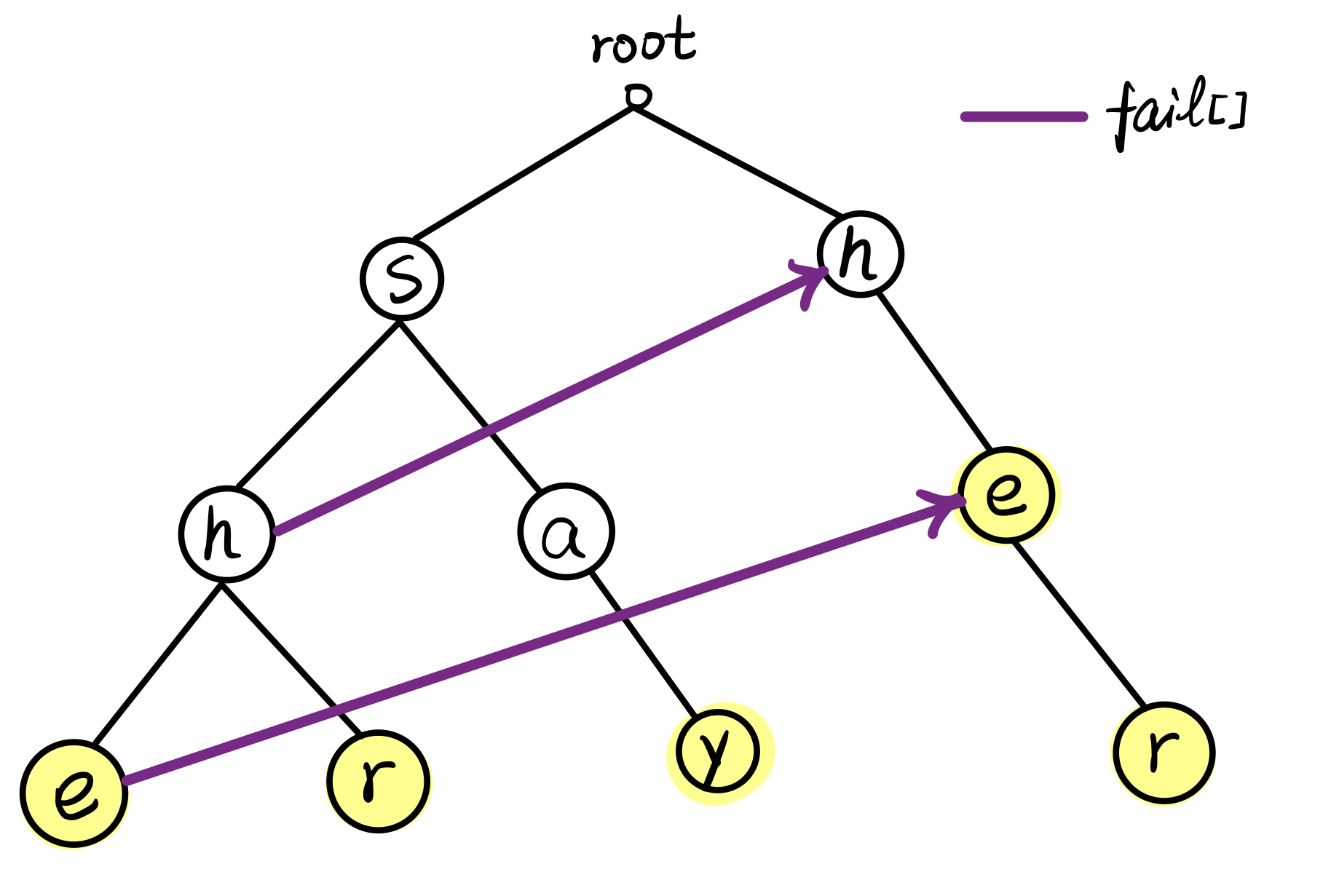
当然，每个结点都应该有自己的 \(fail[]\)，对于 \(fail[u]\) 无法指向其他结点的结点 \(u\)，\(fail[u] = rt\)（\(rt\) 即 \(root\)），就不在图上画了。

求解 \(fail[]\) 的过程（BFS 处理）：

• 结点 \(u\) 上的字符 \(c\)，沿着 \(u\) 父结点的 \(fail[]\) 走，直到到达一个结点，满足该结点的子节点 \(v\) 上的字符也为 \(c\)，则 \(fail[u] = v\)。
• 若跳到根结点也找不到找不到合法的 \(v\)，则 \(fail[u] = rt\)。

代码实现：

void getfail() {
    for (int i = 0; i < 26; i++) {
        if (ch[rt][i]) {
            fail[ch[rt][i]] = rt;
            q.push(ch[rt][i]); 
        }
    }
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = 0; i < 26; i++) {
            if (ch[u][i]) {
                fail[ch[u][i]] = ch[fail[u]][i];
                q.push(ch[u][i]);
            } else ch[u][i] = ch[fail[u]][i];
            /*
            这里为了提高求解 fail[] 的效率，对原 trie 树进行了修改。
            虽不会影响查询，但要明确此时的 trie 树已经不是原来的样子了。
            因此，用求完 fail[] 后的 trie 进行除匹配外的任何操作都要谨慎。
            */
        }
    }
}

匹配代码实现：

int KMP() { //求解出现了多少个模式串
    int n = strlen(s + 1), p = rt, cnt = 0;
    for (int i = 1; i <= n; i++) {
        p = ch[p][s[i] - 'a'];
        for (int k = p; k && flag[k] != -1; k = fail[k]) {
            // 无论匹配成功与否都要跳 fail[]，因为 fail[] 联系的是不同的模式串，都对答案有贡献。
            cnt += flag[k];
            flag[k] = -1;
            // 修改标记，防止重复访问，节省时间。
        }
    }
}

若有 \(n\) 个模式串，最优时间复杂度 \(O(2 \sum\limits_{i = 1}^n |p_i| + |s|)\)，但极端情况下可以到近似 \(O(2 \sum\limits_{i = 1}^n |p_i| + \max\limits_{1 \le i \le n}\{|p_i|\} \times |s|)\)。

模板与优化

洛谷 P3808 【模板】AC 自动机（简单版）

纯纯套板子。

P3796 【模板】AC 自动机（加强版）

把 \(flag[]\) 的值由 \(0 / 1\) 改为对应字符串的下标，对每个字符串单独开一个 \(cnt[]\)，匹配的时候更新出现次数并取最值即可。

匹配代码：

int kmp(char s[]) {
    int n = strlen(s + 1), p = rt, res = 0;
    for (int i = 1; i <= n; i++) {
        p = ch[p][s[i] - 'a'];
        for (int k = p; k; k = fail[k]) {
            if (flag[k]) {
                cnt[flag[k]]++;
                res = max(res, cnt[flag[k]]);
            }
        }
    }
    return res;
}

P5357 【模板】AC 自动机（二次加强版）

数据并不保证任意两个字符串不相同，所以记录每个模式串的末字符结点编号 \(ed[]\) 和每个点的 \(cnt[]\)，最后输出 \(cnt[ed[i]]\)。

一看数据范围，再一看最坏时间复杂度，TLE……

考虑优化。

回到刚刚的图——

如果匹配了左侧的 h，则当前字符再匹配右侧的 h 也会成功，右侧 h 的出现次数也加一。在此基础上，若再匹配了 e，则右侧的 e 的出现次数也加 \(1\)。

以此类推，在匹配过程中不跳 \(fail[]\) 的条件下求得每个结点匹配的次数 \(t[]\) 后，有 \(cnt[u] = \sum\limits_{fail[v] = u} cnt[v] + t[u]\)。

欸，怎么有股树的味道。我们维护树上每个节点的子树大小时，不就是用的 \(sz[u] = \sum\limits_{v \in son(u)} sz[v] + 1\) 吗？可不可以将 \(fail[]\) 看作边，在形成的图上处理这个问题呢？

将每个 \((fail[i], i)\) 都看作一条无向边，就形成了一棵以 \(rt\) 为根的树！一般将其称为 fail 树。

此时，我们在建出来的 fail 树上跑一遍 dfs，便能求出 \(cnt[]\) 啦，时间复杂度也来到了优秀的 \(O(3 \sum\limits_{i = 1}^n |p_i| + |s|)\)。

Bonus：

建图时真的要对每个 \((i, fail[i])\) 都建一条无向边吗？

关注到 fail 树以 \(rt\) 为根，结合 \(fail[]\) 的求解过程可推出在同样以 \(rt\) 为根的 trie 树上， \(dep[fail[i]] < dep[i]\)，进一步可推出在 fail 树上，同样满足 \(dep[fail[i]] < dep[i]\)，因此只需建 \(fail[i] \to i\) 的有向边即可。

\(\text{Code}\)

#include <bits/stdc++.h>

#define MAXN 200100
#define MAXS 2000100

using namespace std;

int n, rt, tot, ch[MAXN][26], fail[MAXN], ed[MAXN];
int tote, head[MAXN], cnt[MAXN];
char s[MAXS];

struct Edge {
    int to, nxt;
} e[MAXN];

template<typename _T>
inline void read(_T &_x) {
    _x = 0;
    _T _f = 1;
    char _ch = getchar();
    while (_ch < '0' || '9' < _ch) {
        if (_ch == '-') _f = -1;
        _ch = getchar();
    }
    while ('0' <= _ch && _ch <= '9') {
        _x = (_x << 3) + (_x << 1) + (_ch & 15);
        _ch = getchar();
    }
    _x *= _f;
}

template<typename _T>
inline void write(_T _x) {
    if (_x < 0) {
        putchar('-');
        _x = -_x;
    }
    if (_x > 9) write(_x / 10);
    putchar('0' + _x % 10);
}

void add(int u, int v) {
    e[++tote] = Edge{v, head[u]};
    head[u] = tote;
}

void getfail() {
    queue<int> q;
    for (int i = 0; i < 26; i++) {
        if (ch[rt][i]) {
            fail[ch[rt][i]] = rt;
            q.push(ch[rt][i]);
        }
    }
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = 0; i < 26; i++) {
            if (ch[u][i]) {
                fail[ch[u][i]] = ch[fail[u]][i];
                q.push(ch[u][i]);
            } else ch[u][i] = ch[fail[u]][i];
        }
    }
}

void dfs(int u) {
    for (int i = head[u], v; i; i = e[i].nxt) {
        v = e[i].to;
        dfs(v);
        cnt[u] += cnt[v];
    }
}

int main() {
    read(n);
    for (int i = 1; i <= n; i++) {
        scanf("%s", s + 1);
        int p = rt;
        for (int j = 1; s[j]; j++) {
            int x = s[j] - 'a';
            if (!ch[p][x]) ch[p][x] = ++tot;
            p = ch[p][x];
        }
        ed[i] = p;
    }
    getfail();
    for (int i = 1; i <= tot; i++) add(fail[i], i);
    scanf("%s", s + 1);
    int p = rt;
    for (int i = 1; s[i]; i++) {
        cnt[p = ch[p][s[i] - 'a']]++;
    }
    dfs(0);
    for (int i = 1; i <= n; i++) {
        write(cnt[ed[i]]), putchar('\n');
    }
    return 0;
}