黑科技：数组两倍空间线段树，实现方便

简介

某天膜 CaptainSlow 代码的时候发现了一个神奇的东西：

inline void Index(int L, int R) { return L + R | L != R; }

通过这个函数寻找线段树节点的下标只需要两倍空间！不动态开点也可以实现两倍空间！

(2021.7.14 更新了正确性证明）

正确性证明

先考虑前面一部分也就是 \(L+R\) 。画个图：

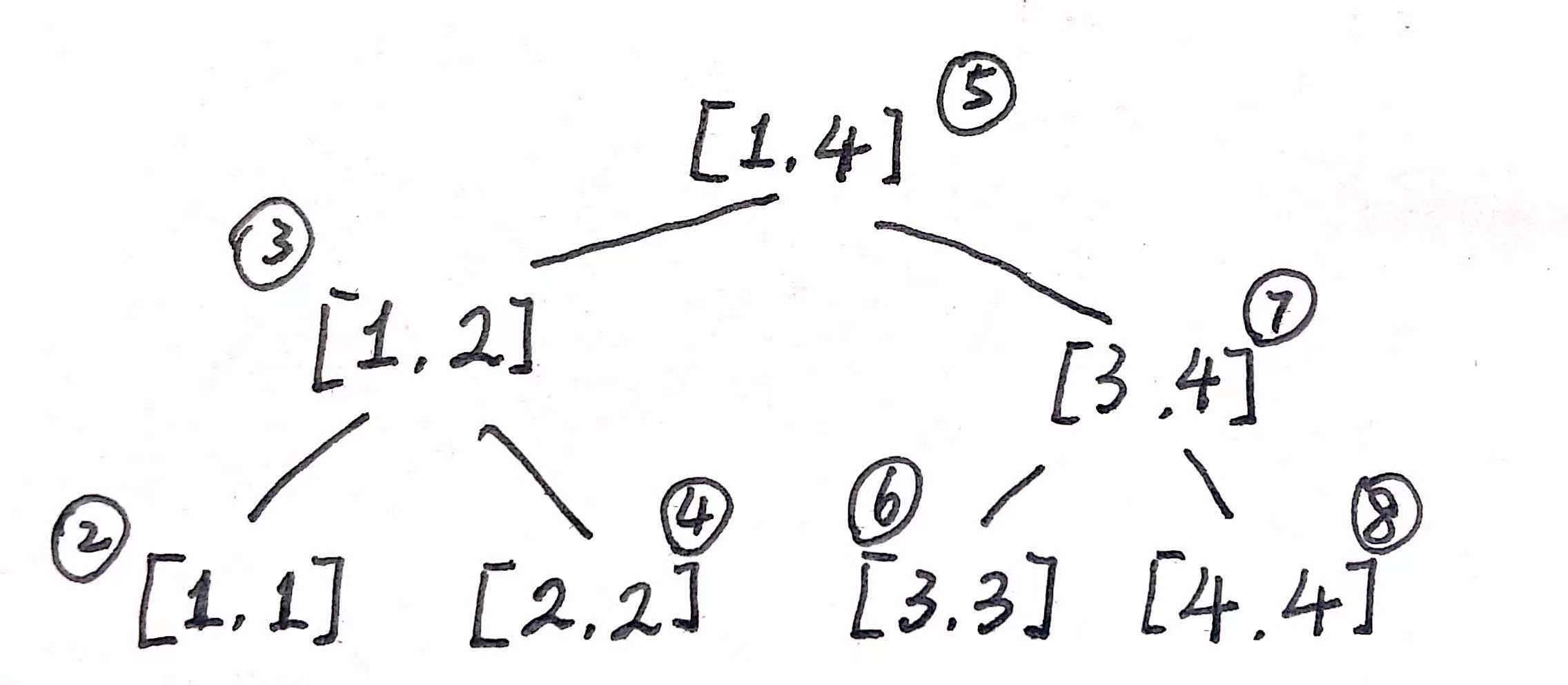
发现若所有区间长度为 \(1\) 或偶数，那么就没有问题了！安排的方式就是中序遍历。当区间长度为奇数时，再画个图：

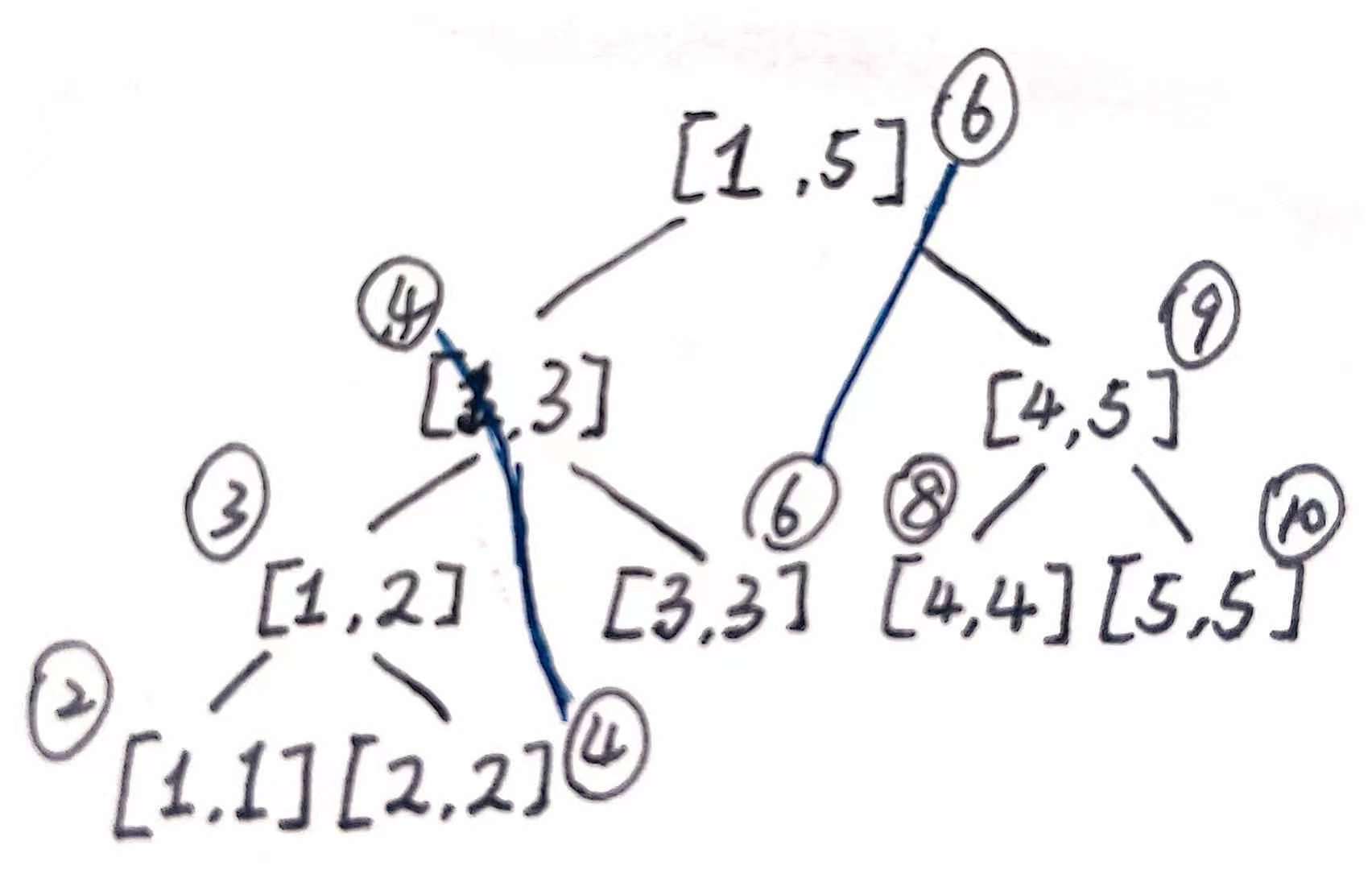
就是说，奇数长度的线段下标按 \(L+R\) 就会和正中间那个叶子节点冲突。那么后面半个式子的作用就来了：

所有叶子节点的 \(L+R\) 都为偶数，不变；偶数长度的区间 \(L+R\) 都为奇数，不变；剩下奇数长度的区间下标加一。对于最后一种情况，由于右半侧下标和至少为 \(L+R+2\) ，所以加一不会有新的重复。

证毕。

例

luogu 3372

#include <cstdio>
#define Maxn 100010

long long T[Maxn << 1], Tag[Maxn << 1], A[Maxn];
int n, q;

inline int Index(int Left, int Right);
inline void Build(int Left, int Right);
inline void Push(int Left, int Right);
inline void Change(int Left, int Right, int L, int R, long long k);
inline long long Query(int Left, int Right, int L, int R);

int main() {
    scanf("%d%d", &n, &q);
    for (int i = 1; i <= n; ++i) scanf("%lld", &A[i]);
    Build(1, n);
    for (int i = 1; i <= q; ++i) {
        int opt, x, y;
        scanf("%d%d%d", &opt, &x, &y);
        if (opt == 1) {
            long long k;
            scanf("%lld", &k);
            Change(1, n, x, y, k);
        } else {
            printf("%lld\n", Query(1, n, x, y));
        }
    }
    return 0;
}

inline int Index(int Left, int Right) {
    return Left + Right | Left != Right;
}

inline void Build(int Left, int Right) {
    if (Left == Right) {
        T[Index(Left, Right)] = A[Left];
        return;
    }
    int Mid = (Left + Right) >> 1;
    Build(Left, Mid);
    Build(Mid + 1, Right);
    T[Index(Left, Right)] = T[Index(Left, Mid)] + T[Index(Mid + 1, Right)];
    return;
}

inline void Push(int Left, int Right) {
    if (Left == Right) return;
    int Mid = (Left + Right) >> 1;
    Tag[Index(Left, Mid)] += Tag[Index(Left, Right)];
    Tag[Index(Mid + 1, Right)] += Tag[Index(Left, Right)];
    T[Index(Left, Mid)] += Tag[Index(Left, Right)] * (Mid - Left + 1);
    T[Index(Mid + 1, Right)] += Tag[Index(Left, Right)] * (Right - Mid);
    Tag[Index(Left, Right)] = 0;
    return;
}

inline void Change(int Left, int Right, int L, int R, long long k) {
    Push(Left, Right);
    if (L <= Left && Right <= R) {
        Tag[Index(Left, Right)] += k;
        T[Index(Left, Right)] += (Right - Left + 1) * k;
        return;
    }
    int Mid = (Left + Right) >> 1;
    if (L <= Mid) Change(Left, Mid, L, R, k);
    if (R > Mid) Change(Mid + 1, Right, L, R, k);
    T[Index(Left, Right)] = T[Index(Left, Mid)] + T[Index(Mid + 1, Right)];
    return;
}

inline long long Query(int Left, int Right, int L, int R) {
    Push(Left, Right);
    if (L <= Left && Right <= R) return T[Index(Left, Right)];
    int Mid = (Left + Right) >> 1;
    if (R <= Mid) return Query(Left, Mid, L, R);
    if (L > Mid) return Query(Mid + 1, Right, L, R);
    return Query(Left, Mid, L, R) + Query(Mid + 1, Right, L, R);
}